C++利用伴随阵法实现矩阵求逆

时间:2023-03-20 convective rain 人气:0

先来一段百度百科上的搜索结果：

伴随阵法

定理：n阶矩阵为可逆的充分必要条件是A非奇异，且：

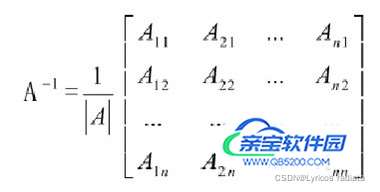
其中，是|A|中元素的代数余子式；矩阵

称为矩阵A的伴随矩阵，记作A*，于是有

用此方法求逆矩阵，对于小型矩阵，特别是二阶方阵求逆既方便、快阵，又有规律可循。因为二阶可逆矩阵的伴随矩阵，只需要将主对角线元素的位置互换，次对角线的元素变号即可。

若可逆矩阵是二阶或二阶以上矩阵，在求逆矩阵的过程中，需要求9个或9个以上代数余子式，还要计算一个三阶或三阶以上行列式，工作量大且中途难免出现符号及计算的差错。对于求出的逆炬阵是否正确，一般要通过来检验。一旦发现错误，必须对每一计算逐一排查。

下面我们来设计一下伴随阵法矩阵求逆的C++代码。

首先，需要自定义一个矩阵类型

#include<vector>
typedef vector<double> vec;
typedef vector<vec> mat;

然后，设计矩阵数乘的代码

mat num_mul(mat A, double num) {
	mat B(A.size(), vec(A[0].size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B[0].size(); j++)
			B[i][j] = A[i][j] * num;
	return B;
}

再写一段计算伴随矩阵的代码

mat cutoff(mat A, int i, int j) {  //切割，划去第1行第i列
	mat B(A.size() - 1, vec(A.size() - 1));
	for(int c = 0; c < B.size(); c++)
		for(int r = 0; r < B.size(); r++)
			B[c][r] = A[c + (c >= i)][r + (r >= j)];
	return B;
}

double det(mat A) {
	if(A.size() == 1)
		return A[0][0];  //当A为一阶矩阵时，直接返回A中唯一的元素
	double ans = 0;
	for(int j = 0; j < A.size(); j++)
		ans += A[0][j] * det(cutoff(A, 0, j)) * (j % 2 ? -1 : 1);
	return ans;
}

mat company_mat(mat A) {
	mat B(A.size(), vec(A.size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B.size(); j++)
			B[j][i] = det(cutoff(A, i, j)) * ((i + j) % 2 ? -1 : 1);  //伴随矩阵与原矩阵存在转置关系
	return B;
}

最后，把我原创的代码分享给大家

#include<iostream>
#include<vector>
using namespace std;
typedef vector<double> vec;
typedef vector<vec> mat;

mat cutoff(mat A, int i, int j) {  //切割，划去第1行第i列
	mat B(A.size() - 1, vec(A.size() - 1));
	for(int c = 0; c < B.size(); c++)
		for(int r = 0; r < B.size(); r++)
			B[c][r] = A[c + (c >= i)][r + (r >= j)];
	return B;
}

double det(mat A) {
	if(A.size() == 1)
		return A[0][0];  //当A为一阶矩阵时，直接返回A中唯一的元素
	double ans = 0;
	for(int j = 0; j < A.size(); j++)
		ans += A[0][j] * det(cutoff(A, 0, j)) * (j % 2 ? -1 : 1);
	return ans;
}

mat company_mat(mat A) {
	mat B(A.size(), vec(A.size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B.size(); j++)
			B[j][i] = det(cutoff(A, i, j)) * ((i + j) % 2 ? -1 : 1);
	return B;
}

void output(mat A) {
	cout << "......\n";
	for(int i = 0; i < A.size(); i++) {
		for(int j = 0; j < A[0].size(); j++)
			printf("%.2lf ", A[i][j]);
		cout << '\n';
	}
	cout << "......\n";
}

mat num_mul(mat A, double num) {
	mat B(A.size(), vec(A[0].size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B[0].size(); j++)
			B[i][j] = A[i][j] * num;
	return B;
}

int main() {
	int n;
	scanf("%d", &n);  //输入阶数
	if(n == 0)
		return 0;
	mat A(n, vec(n));
	for(int i = 0; i < n; i++)
		for(int j = 0; j < n; j++)
			scanf("%lf", &A[i][j]);  //输入A各行各列的元素
	mat B = num_mul(company_mat(A), 1 / det(A));
	output(B);
	return 0;
}

加载全部内容