PyTorch爬山算法

时间:2022-09-28 盼小辉丶人气:0

0. 前言

在随机搜索策略中，每个回合都是独立的。因此，随机搜索中的所有回合都可以并行运行，最终选择能够得到最佳性能的权重。我们还通过绘制总奖励随回合增加的变化情况进行验证，可以看到奖励并没有上升的趋势。在本节中，我们将实现爬山算法 (hill-climbing algorithm)，以将在一个回合中学习到的知识转移到下一个回合中。

1. 使用 PyTorch 实现爬山算法

1.1 爬山算法简介

在爬山算法中，我们同样从随机选择的权重开始。但是，对于每个回合，我们都会为权重添加一些噪声数据。如果总奖励有所改善，我们将使用新的权重来更新原权重；否则，将保持原权重。通过这种方法，随着回合的增加，权重也会逐步修改，而不是在每个回合中随机改变。

1.2 使用爬山算法进行 CartPole 游戏

接下来，我们使用 PyTorch 实现爬山算法。首先，导入所需的包，创建一个 CartPole 环境实例，并计算状态空间和动作空间的尺寸。重用 run_episode 函数，其会根据给定权重，模拟一个回合后返回总奖励：

import gym
import torch
from matplotlib import pyplot as plt
env = gym.make('CartPole-v0')

n_state = env.observation_space.shape[0]
print(n_state)

n_action = env.action_space.n
print(n_action)

def run_episode(env, weight):
    state = env.reset()
    total_reward = 0
    is_done = False
    while not is_done:
        state = torch.from_numpy(state).float()
        action = torch.argmax(torch.matmul(state, weight))
        state, reward, is_done, _ = env.step(action.item())
        total_reward += reward
    return total_reward

模拟 1000 个回合，并初始化变量用于跟踪最佳的总奖励以及相应的权重。同时，初始化一个空列表用于记录每个回合的总奖励：

n_episode = 1000
best_total_reward = 0
best_weight = torch.randn(n_state, n_action)

total_rewards = []

正如以上所述，我们在每个回合中为权重添加一些噪音，为了使噪声不会覆盖原权重，我们还将对噪声进行缩放，使用 0.01 作为噪声缩放因子：

noise_scale = 0.01

然后，就可以运行 run_episode 函数进行模拟。

随机选择初始权重之后，在每个回合中执行以下操作：

为权重增加随机噪音
智能体根据线性映射采取动作
回合终止并返回总奖励
如果当前奖励大于到目前为止获得的最佳奖励，更新最佳奖励和权重；否则，最佳奖励和权重将保持不变
记录每回合的总奖励

for e in range(n_episode):
    weight = best_weight + noise_scale * torch.rand(n_state, n_action)
    total_reward = run_episode(env, weight)
    if total_reward >= best_total_reward:
        best_total_reward = total_reward
        best_weight = weight
    total_rewards.append(total_reward)
print('Episode {}: {}'.format(e + 1, total_reward))

计算使用爬山算法所获得的平均总奖励：

print('Average total reward over {} episode: {}'.format(n_episode, sum(total_rewards) / n_episode))
# Average total reward over 1000 episode: 62.421

2. 改进爬山算法

为了评估使用爬山算法的训练效果，多次重复训练过程，使用循环语句多次执行爬山算法，可以观察到平均总奖励的波动变化较大：

for i in range(10):
    best_total_reward = 0
    best_weight = torch.randn(n_state, n_action)
    total_rewards = []
    for e in range(n_episode):
        weight = best_weight + noise_scale * torch.rand(n_state, n_action)
        total_reward = run_episode(env, weight)
        if total_reward >= best_total_reward:
            best_total_reward = total_reward
            best_weight = weight
        total_rewards.append(total_reward)
        # print('Episode {}: {}'.format(e + 1, total_reward))

print('Average total reward over {} episode: {}'.format(n_episode, sum(total_rewards) / n_episode))

以下是我们运行10次后得到的结果：

Average total reward over 1000 episode: 200.0
Average total reward over 1000 episode: 9.846
Average total reward over 1000 episode: 82.1
Average total reward over 1000 episode: 9.198
Average total reward over 1000 episode: 9.491
Average total reward over 1000 episode: 9.073
Average total reward over 1000 episode: 149.421
Average total reward over 1000 episode: 49.584
Average total reward over 1000 episode: 8.827
Average total reward over 1000 episode: 9.369

产生如此差异的原因是什么呢？如果初始权重较差，则添加的少量噪声只会小范围改变权重，且对改善性能几乎没有影响，导致算法收敛性能不佳。另一方面，如果初始权重较为合适，则添加大量噪声可能会大幅度改变权重，使得权重偏离最佳权重并破坏算法性能。为了使爬山算法的训练更稳定，我们可以使用自适应噪声缩放因子，类似于梯度下降中的自适应学习率，随着模型性能的提升改变噪声缩放因子的大小。

为了使噪声具有自适应性，执行以下操作：

指定初始噪声缩放因子
如果回合中的模型性能有所改善，则减小噪声缩放因子，本节中，每次将噪声缩放因子减小为原来的一半，同时设置缩放因子最小值为 0.0001
而如果回合中中的模型性能下降，则增大噪声缩放因子，本节中，每次将噪声缩放因子增大为原来的 2 倍，同时设置缩放因子最大值为 2

noise_scale = 0.01
best_total_reward = 0
best_weight = torch.randn(n_state, n_action)
total_rewards = []
for e in range(n_episode):
    weight = best_weight + noise_scale * torch.rand(n_state, n_action)
    total_reward = run_episode(env, weight)
    if total_reward >= best_total_reward:
        best_total_reward = total_reward
        best_weight = weight
        noise_scale = max(noise_scale/2, 1e-4)
    else:
        noise_scale = min(noise_scale*2, 2)
    total_rewards.append(total_reward)
    print('Episode {}: {}'.format(e + 1, total_reward))

可以看到，奖励随着回合的增加而增加。训练过程中，当一个回合中可以运行 200 个步骤时，模型的性能可以得到保持，平均总奖励也得到了极大的提升：

print('Average total reward over {} episode: {}'.format(n_episode, sum(total_rewards) / n_episode))
# Average total reward over 1000 episode: 196.28

接下来，为了更加直观的观察，我们绘制每个回合的总奖励的变化情况，如下所示，可以看到总奖励有明显的上升趋势，然后稳定在最大值处：

plt.plot(total_rewards, label='search')
plt.xlabel('episode')
plt.ylabel('total_reward')
plt.legend()
plt.show()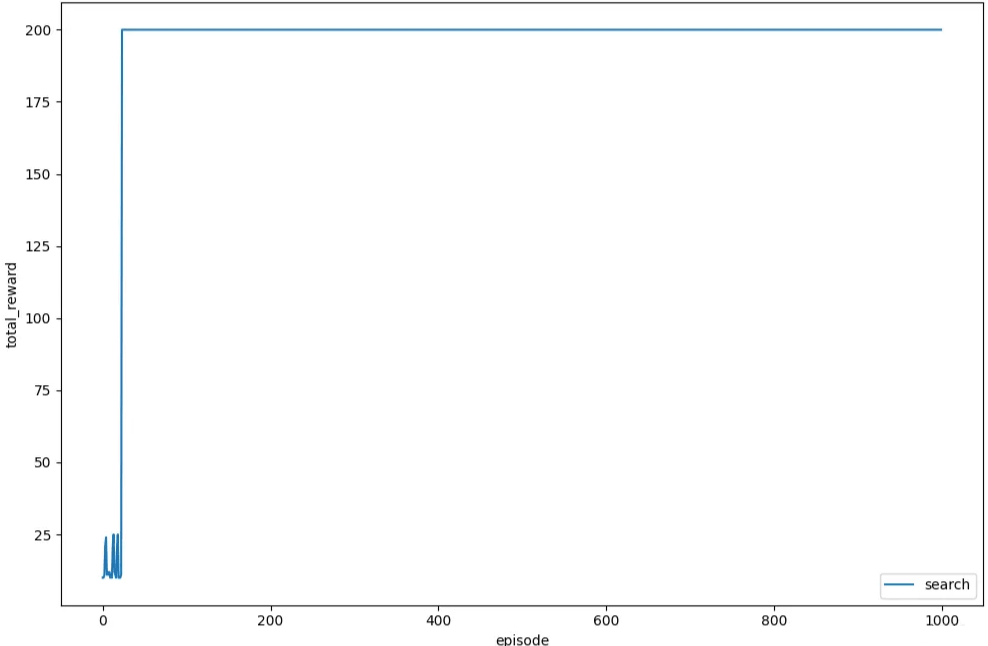

多次运行训练过程过程，可以发现与采用恒定噪声缩放因子进行学习相比，自适应噪声缩放因子可以得到稳定的训练结果。

接下来，我们测试所得到的模型策略在 1000 个新回合中的性能表现：

n_episode_eval = 1000
total_rewards_eval = []
for episode in range(n_episode_eval):
    total_reward = run_episode(env, best_weight)
    print('Episode {}: {}'.format(episode+1, total_reward))
    total_rewards_eval.append(total_reward)

print('Average total reward over {} episode: {}'.format(n_episode_eval, sum(total_rewards_eval)/n_episode_eval))
# Average total reward over 1000 episode: 199.98

可以看到在测试阶段的平均总奖励接近 200，即 CartPole 环境中可以获得的最高奖励。通过多次运行评估，可以获得非常一致的结果。

加载全部内容