Java Dijkstra算法求解最短路径

时间:2022-09-28 洛阳泰山人气:0

算法简介

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学迪家迪杰斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点最短路劲算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

代码实现思路

1.先初始化源节点（起始点）到其他各个拓扑节点的最短距离，可以用map存放，key为节点，value为节点到源节点的距离。

比如数据库中存储的各个拓扑点的信息，我们需要先把数据库各地拓扑点之间的距离，加载出来，用map和矩阵（二维数组）方式。数据库拓扑信息存储表demo：

id	source	target	dist
1	v1	v2	15.67

soure和target为相连的两个拓扑点，dist是相连接的两个拓扑点之间的距离。

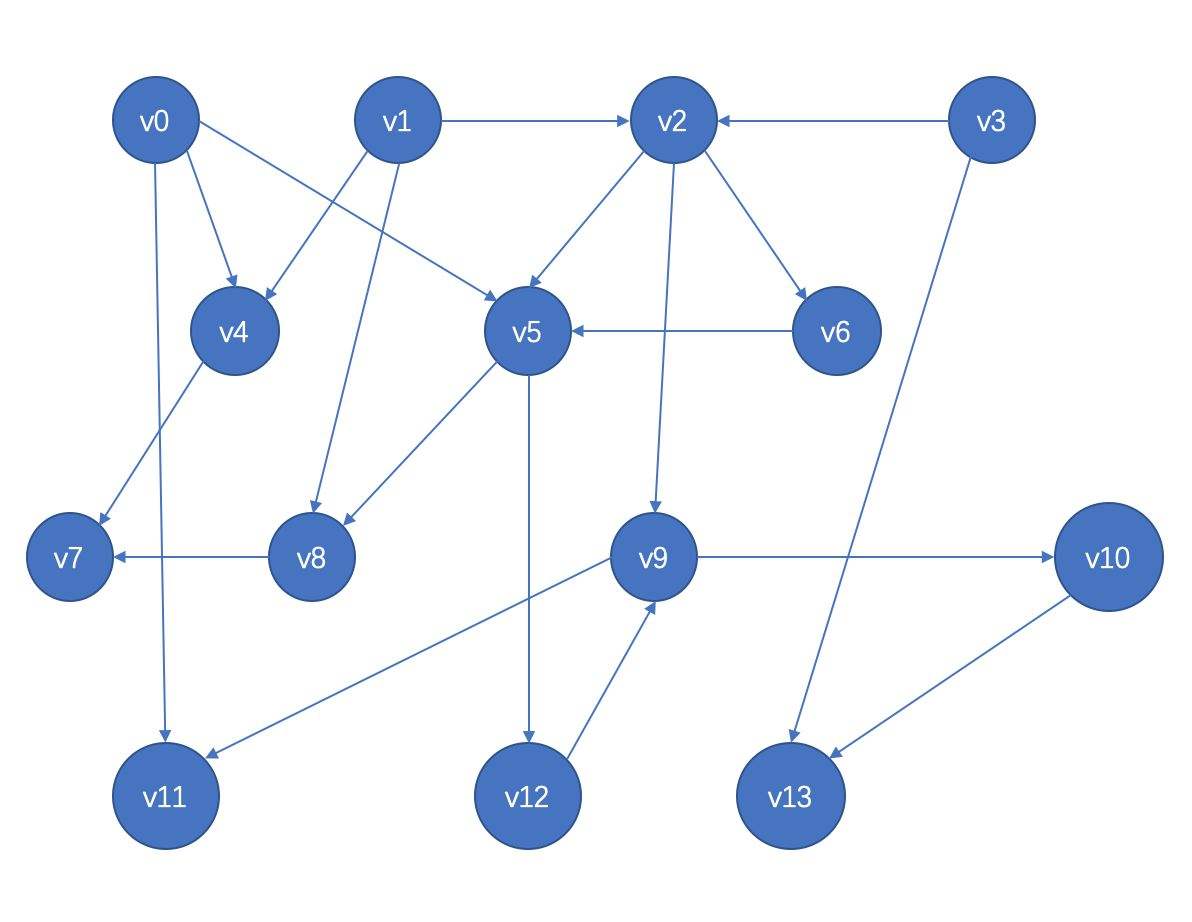
2.初始化源节点到各个节点之间的距离时，源节点到自身节点的距离设为0，到不相连或者间接相连的节点距离设置为最大。

3.从源节点开始，不断循环迭代，各个节点到源节点的最短路线和距离，更新距离map里。当循环遍历到目标节点时，即可求出，源节点到目标节点的最短路线和距离。

更多说明，可以看代码注释。

算法思想

求最短路径步骤 [1]

算法步骤如下： [1]

G={V,E}

1. 初始时令 S={V0},T=V-S={其余顶点}，T中顶点对应的距离值 [1]

若存在，d(V0,Vi)为弧上的权值 [1]

若不存在，d(V0,Vi)为∞ [2]

2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W，加入到S中 [1]

3. 对其余T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值缩短，则修改此距离值 [1]

重复上述步骤2、3，直到S [1] 中包含所有顶点，即W=Vi为止 [1]

代码示例

 
import com.gis.spacedata.domain.entity.tunnel.TunnelTopologyRelEntity;
import lombok.extern.slf4j.Slf4j;
 
import java.util.*;
 
@Slf4j
public class PathUtil {
 
 
    /**
     * 方法描述: 求最短路径
     *
     */
    public static List<Long> dijkstra(List<TunnelTopologyRelEntity> topologies, long start, long end) {
        int size=topologies.size();
        Map<String, Double> distMap = new HashMap<>(size);
        //存放源节点到各个节点的距离key 目标节点，value 源节点到该节点的距离
        Map<Long, Double> dists = new HashMap<>(size);
        //key: 当前节点，value：从原点到达key的最短路径的前驱（上一个）节点
        Map<Long, Long> parent = new HashMap<>(size);
        //被标记最短距离的节点
        Set<Long> markNodes = new HashSet<>(size);
        //获取所有节点列表
        Set<Long> nodes = new HashSet<>(10);
        for (TunnelTopologyRelEntity e : topologies) {
            nodes.add(e.getSource());
            nodes.add(e.getTarget());
            distMap.put(e.getSource() + "-" + e.getTarget(), e.getCost());
        }
        //初始化各个节点到源节点的距离
        for (long node : nodes) {
            if (node == start) {
                dists.put(node, 0d);
            } else {
                dists.put(node, getCost(distMap, start, node));
            }
        }
        // 不断迭代
        while (true) {
            //距离源节点距离最近的节点(还未被标记为离源节点最近的点)
            long closestNode = -1;
            double min = Double.MAX_VALUE;
            for (Map.Entry<Long, Double> entry : dists.entrySet()) {
                if (entry.getValue() < min && !markNodes.contains(entry.getKey())) {
                    min = entry.getValue();
                    closestNode = entry.getKey();
                }
            }
            // 找不到可达的路径了或到达目标点
            if (closestNode == -1 || closestNode==end) {
                break;
            }
            markNodes.add(closestNode);
            for (long node : nodes) {
                double dist = getCost(distMap, closestNode, node);
                // 找到一个为扩展的子节点
                if (dist > 0 && !markNodes.contains(node)) {
                    double new_dist = dists.get(closestNode) + dist;
                    // 新距离小于原始距离，更新
                    if (new_dist < dists.get(node)) {
                        dists.put(node, new_dist);
                        parent.put(node, closestNode);
                    }
                }
            }
        }
        // 倒叙查找到路径
        if (dists.get(end) == Integer.MAX_VALUE) {
            log.info(start + "到" + end + "之间没有最短路径");
            return null;
        } else {
            List<Long> path = new ArrayList<>();
            long current = end;
            path.add(current);
            while (current != start) {
                current = parent.get(current);
                path.add(current);
            }
            //反转
            Collections.reverse(path);
            return path;
        }
    }
 
    /**
     * 方法描述: 获取相邻节点之间距离
     *
     */
    private static double getCost(Map<String, Double> distMap, long start, long end) {
        if (start == end) {
            return 0;
        }
        Double dist1 = distMap.get(start + "-" + end);
        if (dist1 != null) {
            return dist1;
        }
        Double dist2 = distMap.get(end + "-" + start);
        if (dist2 != null) {
            return dist2;
        }
        return Double.MAX_VALUE;
    }
 
 
}

实际业务代码中应用：

public List<Long> getPointShortWay(String startCode, String endCode) {
        TunnelTopologyCodeRelEntity startTopologyCodeRel = getTopologyCodeRel(startCode);
        TunnelTopologyCodeRelEntity endTopologyCodeRel = getTopologyCodeRel(endCode);
        if (Func.isNull(startTopologyCodeRel) || Func.isNull(endTopologyCodeRel)) {
            return Collections.emptyList();
        }
        List<TunnelTopologyRelEntity> list=list();
        return PathUtil.dijkstra(list,startTopologyCodeRel.getId(), endTopologyCodeRel.getId());
    }

加载全部内容