PyTorch随机搜索
盼小辉丶 人气:01. 随机搜索策略
在本节中,我们将学习一种比随机选择动作更复杂的策略来解决 CartPole 问题——随机搜索策略。
一种简单但有效的方法是将智能体对环境的观测值映射到代表两个动作的二维向量,然后我们选择值较高的动作执行。映射函数使用权重矩阵描述,权重矩阵的形状为 4 x 2,因为在CarPole环境中状态是一个 4 维向量,而动作有 2 个可能值。在每个回合中,首先随机生成权重矩阵,并用于计算此回合中每个步骤的动作,并在回合结束时计算总奖励。重复此过程,最后将能够得到最高总奖励的权重矩阵作为最终的动作选择策略。由于在每个回合中我们均会随机选择权重矩阵,因此称这种方法为随机搜索,期望通过在多个回合的测试中找到最佳权重。
2. 使用 PyTorch 实现随机搜索算法
在本节中,我们使用 PyTorch 实现随机搜索算法。
首先,导入 Gym 和 PyTorch 以及其他所需库,并创建一个 CartPole 环境实例:
import gym
import torch
from matplotlib import pyplot as plt
env = gym.make('CartPole-v0')获取并打印状态空间和行动空间的尺寸:
n_state = env.observation_space.shape[0] print(n_state) # 4 n_action = env.action_space.n print(n_action) # 2
当我们在之后定义权重矩阵时,将会使用这些尺寸,即权重矩阵尺寸为 (n_state, n_action) = (4 x 2)。
接下来,定义函数用于使用给定输入权重模拟 CartPole 环境的一个游戏回合并返回此回合中的总奖励:
def run_episode(env, weight):
state = env.reset()
total_reward = 0
is_done = False
while not is_done:
state = torch.from_numpy(state).float()
action = torch.argmax(torch.matmul(state, weight))
state, reward, is_done, _ = env.step(action.item())
total_reward += reward
return total_reward在以上代码中,我们首先将状态数组 state 转换为浮点型张量,然后计算状态数组和权重矩阵张量的乘积 torch.matmul(state, weight),以将状态数组进行映射映射为动作数组,使用 torch.argmax() 操作选择值较高的动作,例如值为 [0.122, 0.333],则应选择动作 1。然后使用 item() 方法获取操作结果值,因为此处的 step() 方法需要接受单元素张量,获取新的状态和奖励。重复以上过程,直到回合结束。
指定回合数,并初始化变量用于记录最佳总奖励和相应权重矩阵,并初始化数组用于记录每个回合的总奖励:
n_episode = 1000 best_total_reward = 0 best_weight = None total_rewards = []
接下来,我们运行 n_episode 个回合,在每个回合中,执行以下操作:
- 构建随机权重矩阵
- 智能体根据权重矩阵将状态映射到相应的动作
- 回合终止并返回总奖励
- 更新最佳总奖励和最佳权重,并记录总奖励
for e in range(n_episode):
weight = torch.rand(n_state, n_action)
total_reward = run_episode(env, weight)
print('Episode {}: {}'.format(e+1, total_reward))
if total_reward > best_total_reward:
best_weight = weight
best_total_reward = total_reward
total_rewards.append(total_reward)运行 1000 次随机搜索获得最佳策略,最佳策略由 best_weight 参数化。在测试最佳策略之前,我们可以计算通过随机搜索获得的平均总奖励:
print('Average total reward over {} episode: {}'.format(n_episode, sum(total_rewards) / n_episode))
# Average total reward over 1000 episode: 46.722可以看到,对比使用随机动作获得的结果 (22.19),使用随机搜索获取的总奖励是其两倍以上。
接下来,我们使用随机搜索得到的最佳权重矩阵,在 1000 个新的回合中测试其表现如何:
n_episode_eval = 1000
total_rewards_eval = []
for episode in range(n_episode_eval):
total_reward = run_episode(env, best_weight)
print('Episode {}: {}'.format(episode+1, total_reward))
total_rewards_eval.append(total_reward)
print('Average total reward over {} episode: {}'.format(n_episode_eval, sum(total_rewards_eval) / n_episode_eval))
# Average total reward over 1000 episode: 114.786随机搜索算法的效果能够获取较好结果的主要原因是 CartPole 环境较为简单。它的观察状态数组仅由四个变量组成。而在 Atari Space Invaders 游戏中的观察值超过 100000 (即 210 \times 160 \times 3210×160×3)。同样 CartPole 中动作状态的维数也仅仅为 2。通常,使用简单算法可以很好地解决简单问题。
我们也可以注意到,随机搜索策略的性能优于随机选择动作。这是因为随机搜索策略将智能体对环境的当前状态考虑在内。有了关于环境的相关信息,随机搜索策略中的动作就可以比完全随机的选择动作更加智能。
我们还可以在训练和测试阶段绘制每个回合的总奖励:
plt.plot(total_rewards, label='search')
plt.plot(total_rewards_eval, label='eval')
plt.xlabel('episode')
plt.ylabel('total_reward')
plt.legend()
plt.show()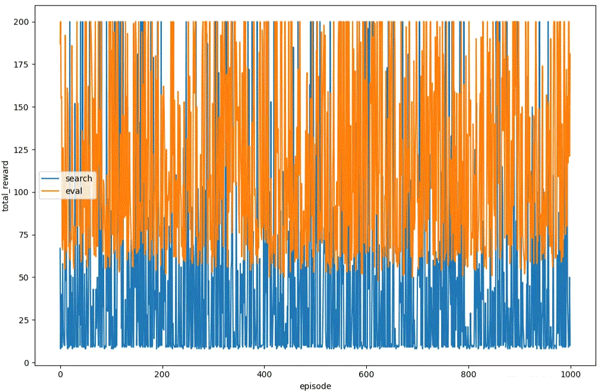
可以看到,每个回合的总奖励是非常随机的,并且并没有因为回合数的增加显示出改善的趋势。在训练过程中,可以看到在实现前期有些回合的总奖励已经可以达到 200,由于智能体的策略并不会因为回合数的增加而改善,因此我们可以在回合总奖励达到 200 时结束训练:
n_episode = 1000
best_total_reward = 0
best_weight = None
total_rewards = []
for episode in range(n_episode):
weight = torch.rand(n_state, n_action)
total_reward = run_episode(env, weight)
print('Episode {}: {}'.format(episode+1, total_reward))
if total_reward > best_total_reward:
best_weight = weight
best_total_reward = total_reward
total_rewards.append(total_reward)
if best_total_reward == 200:
break由于每回合的权重都是随机生成的,因此获取最大奖励的策略出现的回合也并不确定。要计算所需训练回合的期望,可以重复以上训练过程 1000 次,并取训练次数的平均值作为期望:
n_training = 1000
n_episode_training = []
for _ in range(n_training):
for episode in range(n_episode):
weight = torch.rand(n_state, n_action)
total_reward = run_episode(env, weight)
if total_reward == 200:
n_episode_training.append(episode+1)
break
print('Expectation of training episodes needed: ', sum(n_episode_training) / n_training)
# Expectation of training episodes needed: 14.26可以看到,平均而言,我们预计大约需要 14 个回合才能找到最佳策略。
加载全部内容