Java拓扑排序算法
chengqiuming 人气:0拓扑排序原理
1.点睛
一个无环的有向图被称为有向无环图。有向无环图是描述一个工程、计划、生产、系统等流程的有效工具。一个大工程可分为若干子工程(活动),活动之间通常有一定的约束,例如先做什么活动,有什么活动完成后才可以开始下一个活动。
用节点表示活动,用弧表示活动之间的优先关系的有向图,被称为 AOV 网。
在 AOV 网中,若从节点 i 到节点 j 存在一条有向路径,则称节点 i 是节点 j 的前驱,或者称节点 j 是节点 i 的后继。若<i,j>是图中的弧,则称节点 i 是节点 j 的直接前驱,节点 j 是节点 i 的直接后继。
在 AOV 网中弧表示了活动之间存在的制约关系。例如,计算机专业的学生必须完成一系列规定的基础课和专业课才能毕业。学生按照怎样的顺序来学习这些课程呢?
课程的名称与相应编号如下表所示。
| 课程编号 | 课程名称 | 先修课程 |
| C | 程序设计基础 | 无 |
| C1 | 数据结构 | C0、C2 |
| C2 | 离散数学 | C0 |
| C3 | 高级程序设计 | C0、C |
| C4 | 数值分析 | C2、C3、C5 |
| C5 | 高等数学 | 无 |
如果用节点表示课程,用弧表示先修关系,若课程 i 是课程 j 的先修课程,则用弧<i,j>表示,课程之间的关系如下图所示。
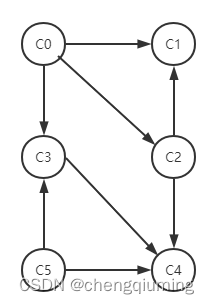
在 AOV 中不允许有环,否则会出现自己是自己的前驱情况,陷入死循环。怎么判断在 AOV 网中是否有环呢?一种检测的办法就是对有向图中的节点进行拓扑排序。如果 AOV 网中的所有节点都在拓扑序列中,则在 AOV 网中必定无环。
2.拓扑排序
拓扑排序指将 AOV 网中的节点排成一个线性序列,该序列必须满足:若从节点 i 到节点 j 有一条路径,则在该序列中节点 i 一定在节点 j 之前。
拓扑排序的基本思想:
1 选择一个无前驱的节点并输出。
2 从图中删除该节点和该节点所有发出边。
3 重复步骤1、2,直到不存在无前驱的节点。
4 如果输出的节点数少于 AOV 网中节点数,则说网中有环,否则输出的序列即拓扑序列。
拓扑排序并不是唯一的,例如上图中,节点 C0 和 C5 都无前驱,先输出哪一个都可以。
下面图解是其中一种删除顺序。

拓扑序列为:C0、C5、C3、C2、C1、C4
在上述过程中有删除节点和边的操作,实际上,没必要真的删除节点和边。可以将没有前驱的节点(入度为0)暂存到栈中,输出时出栈即表示删除。进行边的删除时将其邻接点的入度减1即可。例如下图中删除 C0 的所有发出边,相对于 C3、C2、C1 节点入度减1。
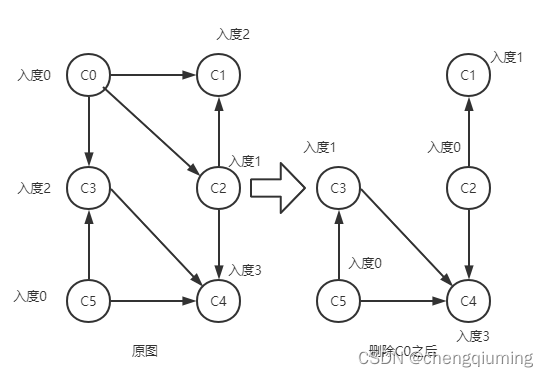
3.算法步骤
1 求各节点的入度,将其存入数组 indegree[] 中,并将入度为 0 的节点入栈 S。
2 如果栈不空,则重复执行以下操作:将栈顶元素 i 出栈并保存到拓扑序列数组 topo[] 中;将节点 i 的所有邻节点入度都减 1,如果减 1 后入度为 0,则立即入栈 S。
3 如果输出的节点数少于 AOV 网中的节点数,则说明网中有环,否则输出拓扑序列。
4.图解
AOV 网如下图所示。
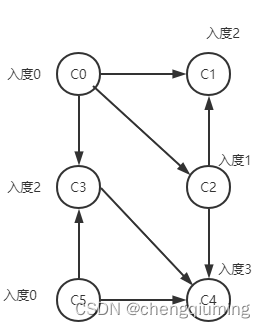
1 输入边时,累加节点入度并保存到数组 indegree[] 中,将入度为0 的节点入栈 S。

2 将栈顶元素 5 出栈并保存到拓扑序列数组 topo[] 中。将节点 5 的所有邻接点(C3、C4)入度都减1,如果减1后,入度为0,则立即入栈 S。

3 将栈顶元素 0 出栈并保存到拓扑序列数组 topo[] 中。将节点 0 的所有邻接点(C1、C2、C4)入度都减1,如果减1后,入度为0,则立即入栈 S。

4 将栈顶元素 3 出栈并保存到拓扑序列数组 topo[] 中。将节点 3 的所有邻接点(C4)入度都减1,如果减1后,入度为0,则立即入栈 S。
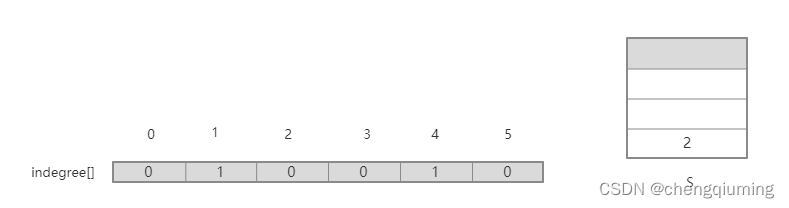
5 将栈顶元素 2 出栈并保存到拓扑序列数组 topo[] 中。将节点 2 的所有邻接点(C1、C4)入度都减1,如果减1后,入度为0,则立即入栈 S。

6 将栈顶元素 4 出栈并保存到拓扑序列数组 topo[] 中。节点 4 没有邻接点。
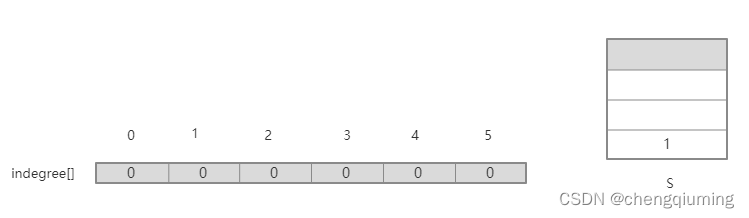
7 将栈顶元素 1 出栈并保存到拓扑序列数组 topo[] 中。节点 1 没有邻接点。
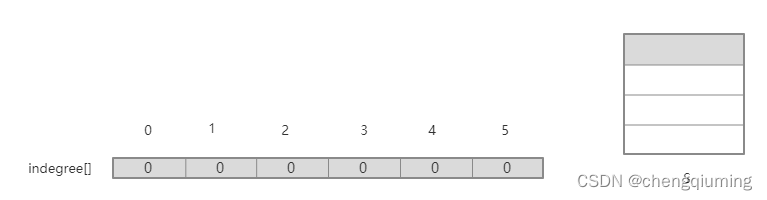
8 栈空,算法停止。输出拓扑排序序列。

拓扑排序算法实现
1.拓扑图
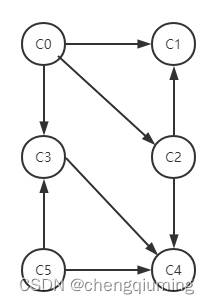
2.实现代码
package graph.topoSort;
import java.util.Scanner;
import java.util.Stack;
public class TopoSort {
static final int maxn = 105;
static int map[][] = new int[maxn][maxn];
static int indegree[] = new int[maxn];
static int topo[] = new int[maxn];
static int n, m;
static Stack<Integer> s = new Stack<>();
static boolean TopoSort() { // 拓扑排序
int cnt = 0;
for (int i = 0; i < n; i++)
if (indegree[i] == 0)
s.push(i);
while (!s.empty()) {
int u = s.peek();
s.pop();
topo[cnt++] = u;
for (int j = 0; j < n; j++)
if (map[u][j] == 1)
if (--indegree[j] == 0)
s.push(j);
}
if (cnt < n) {
return false;
}
return true;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 0; i < m; i++) {
int u, v;
u = scanner.nextInt();
v = scanner.nextInt();
map[u][v] = 1;
indegree[v]++;
}
TopoSort();
for (int i = 0; i < n - 1; i++)
System.out.print(topo[i] + " ");
System.out.println(topo[n - 1]);
}
}3.测试
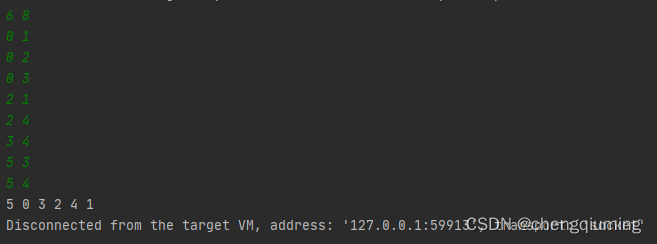
加载全部内容