C语言数据结构堆排序
_奇奇 人气:0“大弦嘈嘈如急雨,小弦切切如私语”“嘈嘈切切错杂弹,大珠小珠落玉盘”
C语言朱武大战数据结构专栏
TOP.堆排序前言
什么是堆排序?假如给你下面的代码让你完善堆排序,你会怎么写?你会怎么排?
void HeapSort(int* a, int n)
{
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizoef(arr[0]);
HeapSort(arr, sz);
return 0;
}
堆排序就是利用堆这个数据结构,对一组数据进行排序。
所以说,堆排序整体分两步完成。
第一步,建堆
第二步,进行排序
注意:以下代码针对的是对一组 数据 排升序
一、向下调整堆排序
对的,向下调整方法,是最优秀的堆排序。
不是太想介绍那种向上调整拉胯的堆排序,我们经常用的是这种优秀的向下排序。
二者区别在于建堆的方法不同。一个是向下建堆O(N),一个是向上建堆O(N*logN)。
具体证明用到了高中 简单的数列公式。
1.向下调整建堆
建堆的技巧
向下建堆也有两种情况。
1.建大堆
2.建小堆
那么到底建大堆还是小堆呢?
解释:建堆在于你是想要排升序,还是排降序。假如建的大堆,因为堆顶的数是最大的,在我们对堆 向下调整排序时,这时候每次都需要把最大的交换到堆底。所以导致最后堆的顺序是升序。
建大堆前
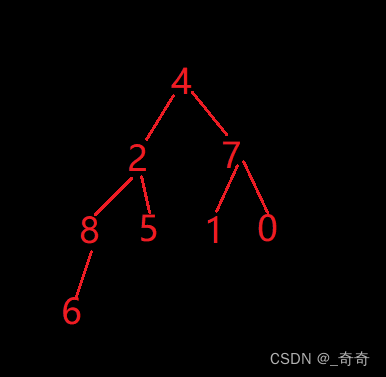
建大堆后

向下调整排序后
此时数组就有序了。
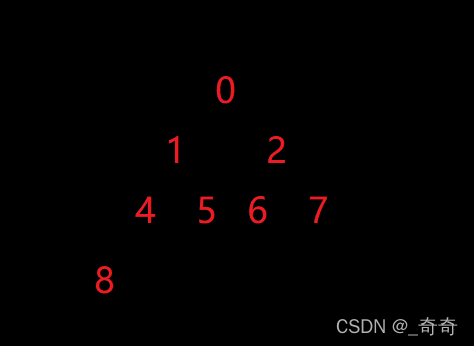
结论:实质是在数组上建堆。排升序建大堆,排降序建小堆。
建堆思路代码
思路:
因为叶子结点本身就是一个大堆,所以从最后一个叶子结点的父亲结点开始进行向下建堆。
这样就能够保证每次建的堆都是大堆。
注意:
1.注意循环结束条件,和if语句里的边界问题child + 1 < n
2.注意完全二叉树父子关系公式
#include <stdio.h>
//交换
void swap(int* x, int* y)
{
int t = 0;
t = *x;
*x = *y;
*y = t;
}
//向下调整
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
//每次调整都需要从左右两边选出孩子最大的那个
//假设坐孩子较大,选出左右孩子大的那个
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
//开始调整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
//不满足就跳出,开始下次for循环调整。
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向下调整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
return 0;
}
2.向下调整排序
调整思路
1.从堆底依次 和 堆顶的数据进行交换。
2.对交换后的 堆顶的值 进行向下调整。向下调整时请无视交换到堆底那个最大的值。
3.继续循环第一步和第二步,直到到正数第二个数结束。
排序整体代码
void swap(int* x, int* y)
{
int t = 0;
t = *x;
*x = *y;
*y = t;
}
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
//每次调整都需要从左右两边选出孩子最大的那个
//假设坐孩子较大,选出左右孩子大的那个
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
//开始调整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
//不满足就跳出,开始下次for循环调整。
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向下调整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//向下调整排序
int end = 0;
for (end = n-1; end > 0; end--)
{
swap(&a[0], &a[end]);
//向下调整时无视最大的那个值,所以end是n-1。
AdjustDown(a, end, 0);
}
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
return 0;
}
3.时间复杂度(难点)
向下建堆O(N)
//向下调整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
很多人的误区在于他的时间复杂度是N*Log2N。这是错误的。
时间复杂度的计算是看思想,而不是看循环猜测。
当是满二叉树,在最坏的情况下,除了最后一层,上面所有层都需要进行向下调整。
最坏情况下的调整次数 = 每层数据个数 * 向下调整次数
第一层向下调整次数是h-1,节点个数是21-1
第二层向下调整次数是h-2, 节点个数是22-1
第h-1层向下调整次数是1,节点个数是2h-1-1
所以总的调整次数为n:n = 20*(h-1) + 21 *(h-2)+… + 2h-1-1 *(1)
根据高中错位相减得到 n = 1−h+21+22+…+2h−2+2h−1
由等比数列前n项和得到 n = 2h−h−1
由二叉树性质N=2h−1和 h = log2(N+1) 得到 n=N−log2(N+1)
大O渐进表示法为n= O(N)
向下调整(N*LogN)
需要向下调整n-1次。每次需要调整的高度为LogN,N为节点的个数,因为节点个数每次少一个。
所以n-1次调整总次数 = log2+log3+…+log(n-1)+log(n)≈log(n!)
由数学知识得log(n!)和nlog(n)是同阶函数。
所以向下调整排序时间复杂度为N*LogN
所以堆排序时间复杂度为:N + N*LogN
大O渐进表示法为:O(N*LogN)
总结:堆排序时间复杂度 O(N*LogN)
二、向上调整堆排序
向上调整排序和向下调整排序的唯一不同在于建堆的不同,导致二者的建堆的时间复杂度略微不同。
1.向上调整建堆
向上调整建堆时间复杂度为N*LogN.具体原因还需要经过残酷的数学计算。孩子不会啊。但是经过网上查阅资料我又找到了计算方法。如图。
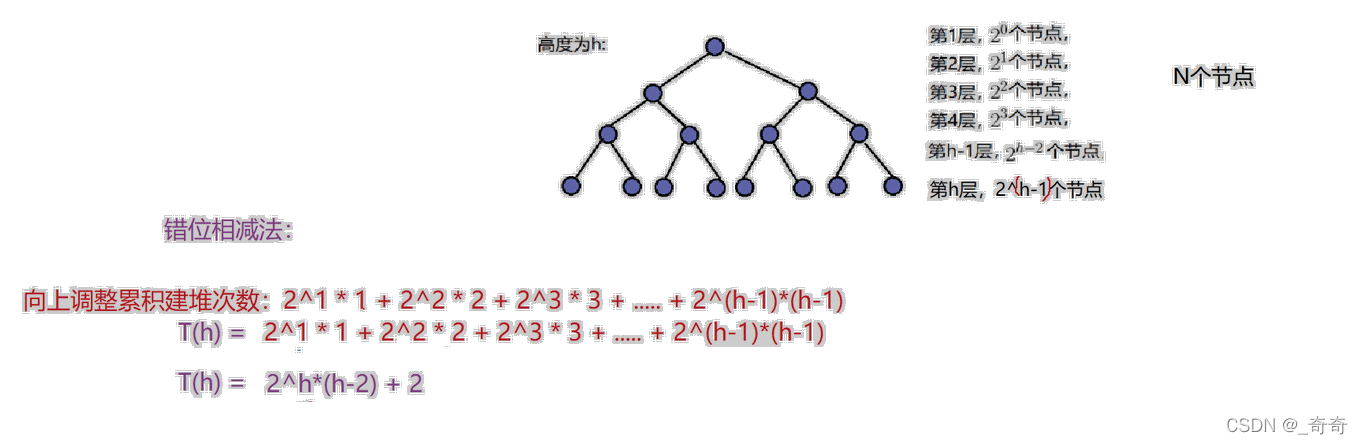
根据二叉树的性质:h = Log2(N+1)
可以将T(h) = 2h * (h-2) + 2换为:
所以总体来说就是向上调整的建堆时间复杂度为O(N * LogN).
2.建堆代码
思路:从第二个元素开始,只关注前两个元素建堆,然后再依次增加元素建堆,使它一直为堆。
向上调整建堆虽然时间复杂度略高,但是代码相对于向下调整简单一点点。
void AdjustUp(int* a, int child)
{
//先把父亲节点表示出来。
int parent = (child - 1) / 2;
while (child > 0)
{
//比较孩子和父亲,开始向上调整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
加载全部内容