C++ 回溯算法
ymz123_ 人气:1迷宫问题
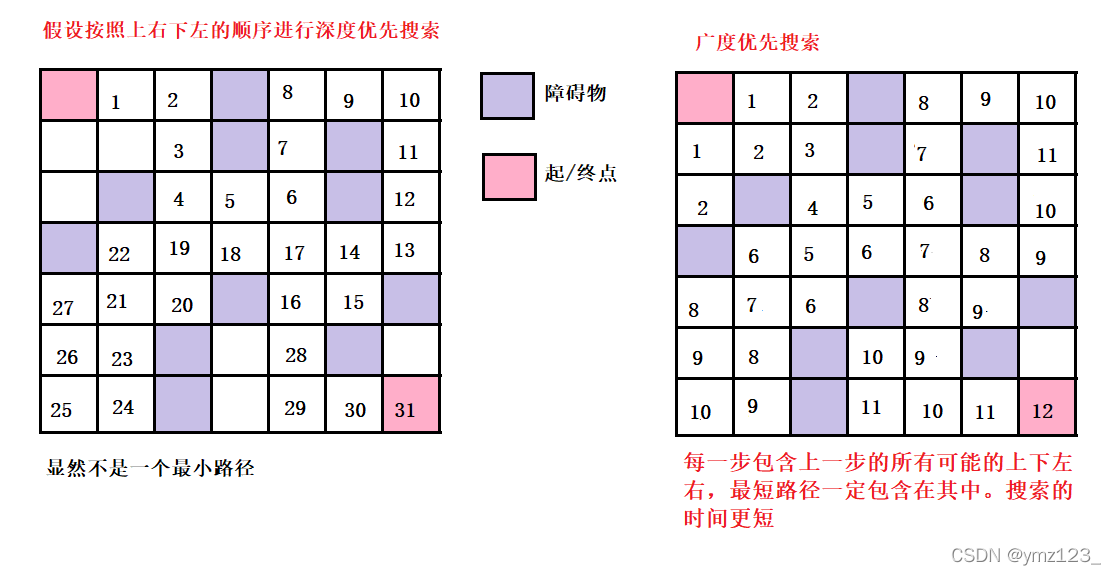
假设有一个迷宫,里面有障碍物,迷宫用二维矩阵表示,标记为0的地方表示可以通过,标记为1的地方表示障碍物,不能通过。现在给一个迷宫出口,让你判断是否可以从入口进来之后,走出迷宫,每次可以向任意方向走。
代码实现:
namespace BFS {
struct pair {
int _x;
int _y;
pair(int x, int y)
:_x(x)
, _y(y)
{}
};
bool mapBFS(vector<vector<int>> mat, int sx, int sy, int ex, int ey)
{
int row = mat.size();
int col = mat[0].size();
queue<pair> q;
q.push(pair(sx, sy));
vector<vector<int>> book(row, vector<int>(col, 0));
book[sx][sy] = 1;
int nextP[4][2] = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
while (!q.empty())
{
pair curPos = q.front();
q.pop();
if (curPos._x == ex && curPos._y == ey)
return true;
//一个点的所有可能延伸的点
for (int i = 0; i < 4; i++)
{
int curX = curPos._x + nextP[i][0];
int curY = curPos._y + nextP[i][1];
if (curX < 0 || curX >= row || curY < 0 || curY >= col)
continue;
//没有走过且不是障碍物
if (mat[curX][curY] == 0 && book[curX][curY] == 0)
{
book[curX][curY] = 1;
//保存新的位置
q.push(pair(curX, curY));
}
}
}
return false;
}
}
int main()
{
vector<vector<int>> mat{ {0, 0, 1, 0},
{1, 0, 0, 1},
{0, 0, 0, 0},
{1, 1, 0, 0} };
int sx, sy, ex, ey;
cin >> sx >> sy >> ex >> ey;
cout << BFS::mapBFS(mat, sx, sy, ex, ey);
return 0;
}
N叉树的层序遍历
问题描述:
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。 树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
代码实现:
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> result;
if(!root)
return result;
queue<Node*> q;
q.push(root);
while(!q.empty())
{
//获取队列中的元素个数
int sz = q.size();
vector<int> rowV;
while(sz--)
{
//保存当前元素在同一行
Node* node = q.front();
q.pop();
rowV.push_back(node->val);
//当前元素的孩子结点入队
for(auto e : node->children)
{
q.push(e);
}
}
result.push_back(rowV);
}
return result;
}
};
腐烂的橘子
问题描述:
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
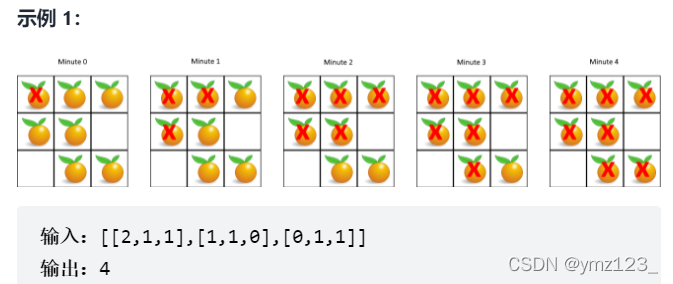
本题可以先找到所有的腐烂橘子入队,用第一批带出新一批腐烂的橘子。 每一批橘子都会在一分钟之内腐烂,所以此题可以转化为求BFS执行的大循环的次数。这里的step的更新需要有一个标记,只有新的腐烂的橘子加入,step才++ 最后BFS执行完,说明所有可以被腐烂的都完成了,再去遍历grid,如果还有值为1的,说明没有办法全部腐烂,返回-1,如果没有,则返回step
代码实现:
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int step = 0;
int row = grid.size();
int col = grid[0].size();
queue<pair<int, int>> q;
//把所有腐烂的橘子入队
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == 2)
q.push(make_pair(i, j));
}
}
static int nextP[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0 ,1}};
while(!q.empty()){
int sz = q.size();
bool flag = false;
while(sz--){
pair curPos = q.front();
q.pop();
for(int i = 0; i < 4; i++){
int curX = curPos.first + nextP[i][0];
int curY = curPos.second + nextP[i][1];
if(curX < 0 || curX >= row || curY < 0 || curY >= col)
continue;
if(grid[curX][curY] == 1){
flag = true;
grid[curX][curY] = 2;
q.push(make_pair(curX, curY));
}
}
}
if(flag)
++step;
}
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == 1)
return -1;
}
}
return step;
}
};
单词接龙
问题描述:
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出:5
解释:一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。
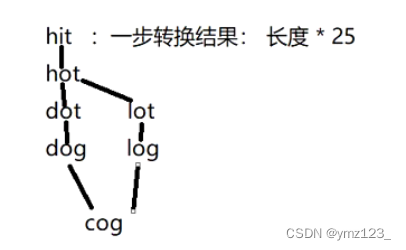
1.通过BFS,首先用beginWord带出转换一个字符之后所有可能的结果
2.每一步都要把队列中上一步添加的所有单词转换一遍,最短的转换肯定在这些单词中,所有这些词的转换只能算一次转换,因为都是上一步转换出来的,这里对于每个单词的每个位置都可以用26个字母进行转换,所以一个单词一次转换的可能有:单词的长度*25
3.把转换成功的新词入队,进行下一步的转换
4.最后整个转换的长度就和BFS执行的次数相同
需要判断单词有没有被搜索过,是一个查询的过程,可以用哈希表
代码实现:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
int step = 1;
unordered_set<string> book;
unordered_set<string> dict;
book.insert(beginWord);
for(string& ch : wordList)
dict.insert(ch);
queue<string> q;
q.push(beginWord);
while(!q.empty()){
int size = q.size();
while(size--){
string curStr = q.front();
q.pop();
if(curStr == endWord)
return step;
for(int i = 0; i < curStr.size(); i++){
string str1 = curStr;
for(char ch = 'a'; ch <= 'z'; ++ch){
str1[i] = ch;
//判断新的单词是否在词典中,且没被搜索过
if(dict.find(str1) != dict.end()
&& book.find(str1) == book.end()){
q.push(str1);
book.insert(str1);
}
}
}
}
++step;
}
return 0;
}
};
打开转盘锁
问题描述:
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0', ‘1', ‘2', ‘3', ‘4', ‘5', ‘6', ‘7', ‘8', ‘9' 。每个拨轮可以自由旋转:例如把 ‘9' 变为 ‘0',‘0' 变为 ‘9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
深度优先不适合此题,递归深度太大,会导致栈溢出。
本题的密码为4位密码,每位密码可以通过拨动一次进行改变,注意这里的数的回环以及拨动的方向拨动方向:向前,向后。
回环:如果当前是9,0时,向前,向后拨动需要变成最小最大,而不是简单的自加自减。
0000一步旋转后的结果有:
0001 0009 0010 0090 0100 0900 1000 9000
代码实现:
class Solution {
public:
int openLock(vector<string>& deadends, string target) {
unordered_set<string> deaddict(deadends.begin(), deadends.end());
//如果0000在死亡数字中,则永远也到不了
if(deaddict.find("0000") != deaddict.end())
return -1;
queue<string> q;
q.push("0000");
//添加标记,已经搜索过的字符不再搜索
unordered_set<string> book;
book.insert("0000");
int step = 0;
while(!q.empty()){
int size = q.size();
while(size--){
string curStr = q.front();
q.pop();
if(curStr == target)
return step;
for(int i = 0; i < 4; i++){
string s1 = curStr;
string s2 = curStr;
//向前或向后旋转
s1[i] = s1[i] =='0' ? '9' : --s1[i];
s2[i] = s2[i] =='9' ? '0' : ++s2[i];
if(deaddict.find(s1) == deaddict.end()
&& book.find(s1) == book.end()){
q.push(s1);
book.insert(s1);
}
if(deaddict.find(s2) == deaddict.end()
&& book.find(s2) == book.end()){
q.push(s2);
book.insert(s2);
}
}
}
++step;
}
return -1;
}
};
加载全部内容