C语言 排序算法
程序猿教你打篮球 人气:0进入正式内容之前,我们先了解下初阶常见的排序分类 :我们今天讲前四个!
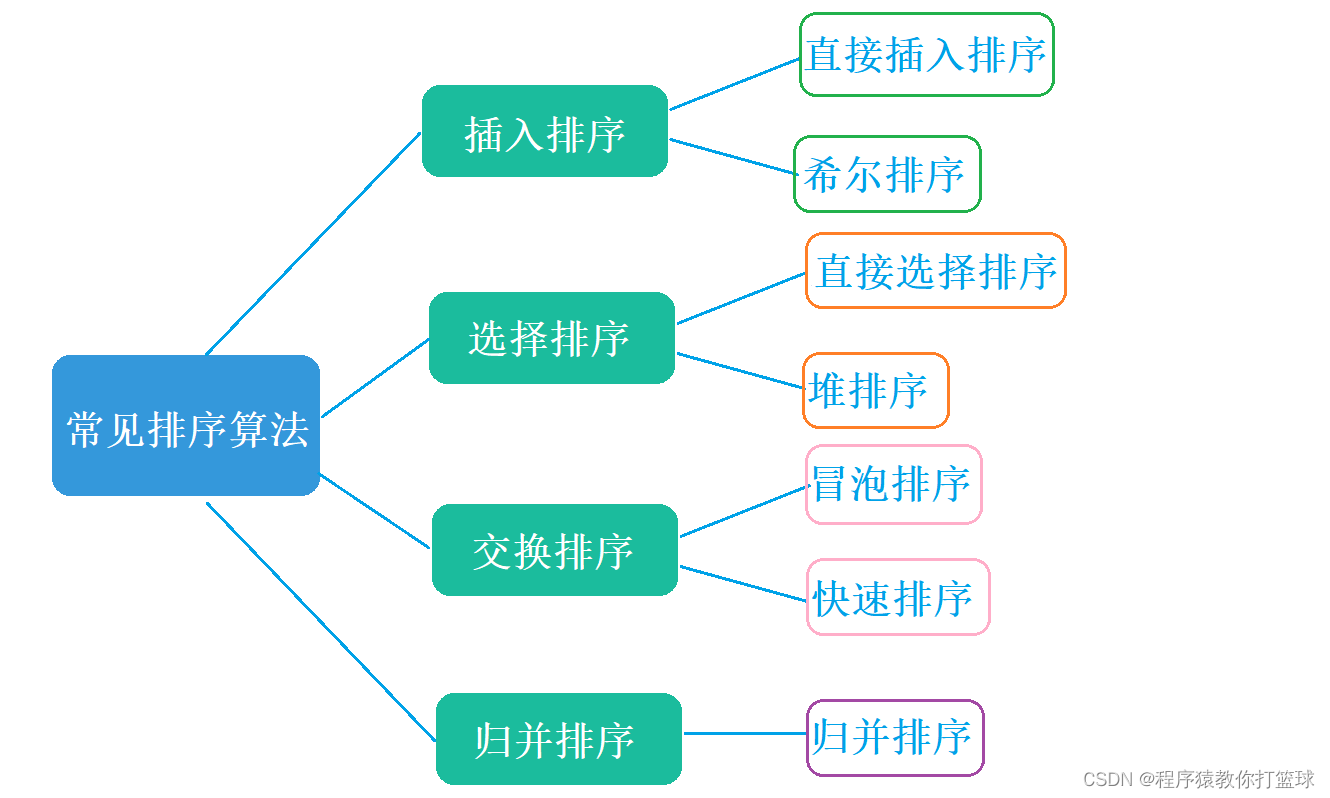
1、直接插入排序
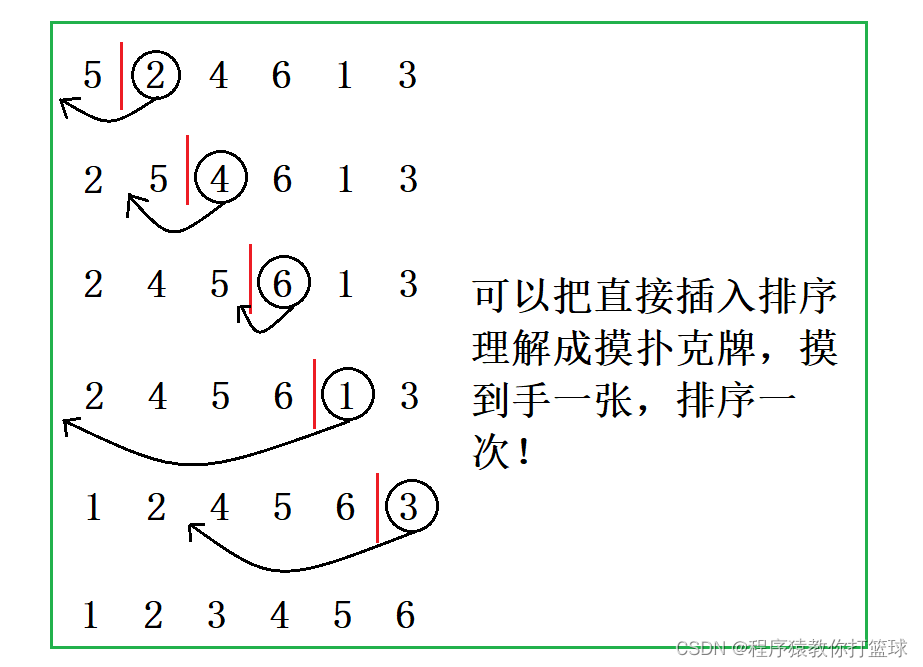
基本思想:当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排 序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移!
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2) 、空间复杂度:O(1)
3. 稳定性:稳定
void InsertSort(int* a, int n)
{
//直接插入排序 ———— 升序
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (a[i] > tmp) //如果比tmp大的话就往后移
{
a[end + 1] = a[end];
--end;
}
else //如果tmp比当前元素大的话就不需要交换位置了,直接跳出循环!
{
break;
}
}
a[end + 1] = tmp; // 最后把tmp放到比他小的元素后面!
}
}2、希尔排序(缩小增量排序)
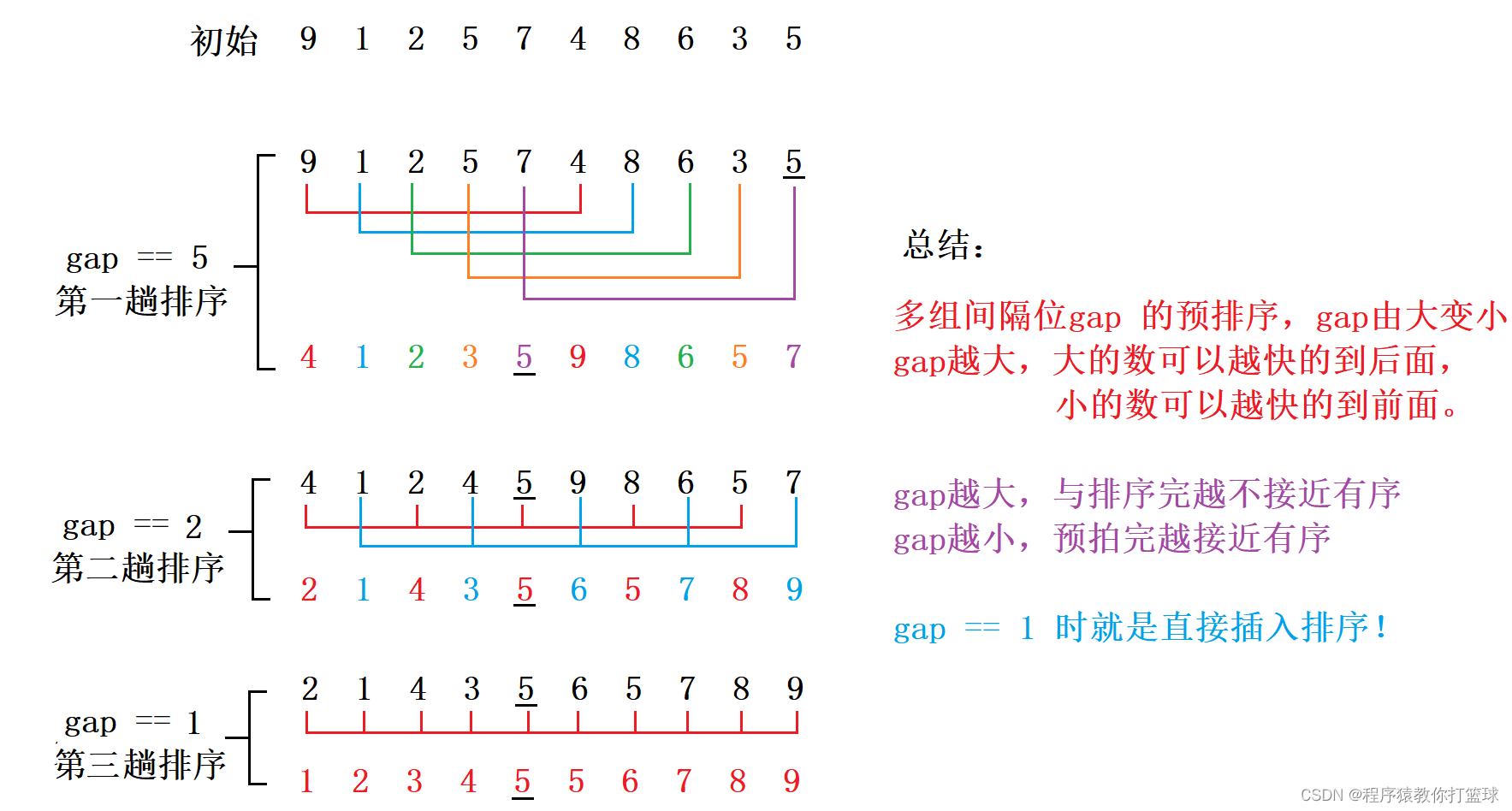
基本思想:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后重复分组和排序的工作。当到达gap=1时,所有记录在统一组内排好序。
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的 了,这样就会很快。这样整体而言,可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3— N^2)
4. 稳定性:不稳定
void ShellSort(int* a, int n)
{
//希尔排序————升序
int gap = n;
while (gap > 1)
{
gap = gap / 2;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
a[end + gap] = tmp;
}
}
}
}3、直接选择排序
基本思想:
在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换 在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
直接选择排序的特性总结:(因为特别简单就不画图了直接上代码)
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2) 、空间复杂度:O(1)
3. 稳定性:不稳定
这里我们用一个优化版本,每次确定两个数的最终位置:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min = begin;
int max = begin;
for (int i = begin; i <= end; ++i)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
Swap(&a[min], &a[begin]);
if (max == begin) //如果max等于begin的话就证明最大值是begin的位置
//需要修正max的位置
{
max = min;
}
Swap(&a[max], &a[end]);
++begin;
--end;
}
}4、堆排序
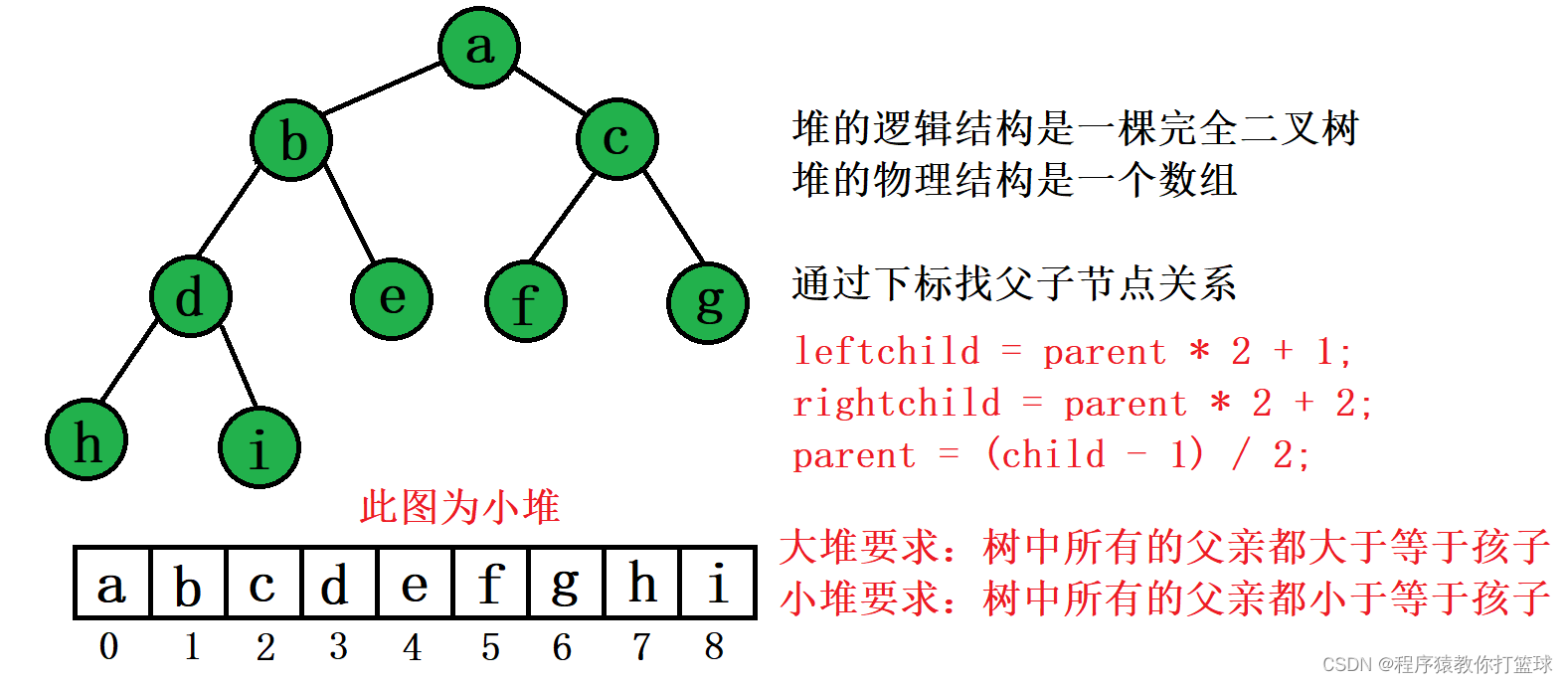
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的 一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
堆排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN) 、空间复杂度:O(1)
3. 稳定性:不稳定

void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] < a[child + 1])
{
child = child + 1;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}建议小伙伴们看完之后一定要自己尝试画图,以及代码练习!如果前面C语言代码量不多的话,写起来也会很吃力的!里面也涉及到了二叉树的相关知识,如果有疑问可以直接联系我!
小伙伴们,咱们软件这一行,实力才是硬道理,爱打篮球的程序猿想送你们一句话:虽然过去不能改变,但未来可以!加油,趁现在!
gitee(码云):Mercury. (zzwlwp) - Gitee.com
加载全部内容