C++回溯算法之深度优先搜索详细介绍
子夜的星 人气:0一、前言
本文介绍了经典搜索算法: 深度优先搜索(DFS)
两个小故事:
岳云鹏的相声:孙越的爸爸带他参观家里面的聚宝盆,走到了一个密室门前,密室的门上上了一把锁,孙越的爸爸身上带了一万多把钥匙,他还忘了哪一把钥匙能打开个门了,于是就一把把试,试到了最后一把,门开了。
你叫DFS,在一次校园活动中你认识了三个非常漂亮的女孩,你想和她们进一步发展。于是,你选择了其中一个人,并对她展开了追求,你采用了 聊天->约会->表白 的恋爱三部曲。但是很不幸,她拒绝了你,于是你添加了第二个女生的微信,同样采取了你常用的三部曲。很不幸,第二个女生也拒绝你了。但是,你没有被困难打倒,于是你添加了第三个女生的微信,依旧是这三部曲,终于,第三个女生答应了你。你的朋友询问你,是如何找到女朋友的?,你答:我采用了DFS对象法
二、基本概念
1.简单介绍
前言中的两个小故事,孙越的爸爸找钥匙开门的过程和DFS小朋友找女朋友都是一个搜索过程。
简而言之,搜索就是尝试问题中所有的可能性,在所有的可能性中找到正确的结果。而深度优先搜索用一句话概括就是:“ 一直往下走,走到最后还是走不通,那就换条路再走,直到无路可走。”用一个成语来形容,那就是 :“ 不撞南墙不回头。”
2.官方概念
以下是维基百科上的解释:
深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。这种算法不会根据图的结构等信息调整执行策略
三、动图分析
DFS会从初始节点出发,按预定的顺序扩展到下一个节点,然后从下一节点出发继续扩展新的节点,不断递归执行这个过程,直到某个节点不能再扩展下一个节点为止。此时,则返回上一个节点重新寻找一个新的扩展节点。如此搜索下去,直到找到目标节点,或者搜索完所有节点为止。
动图:
四、模板框架
以下模板来自于大佬Carl:
void DFS(参数){
if (终止条件){
做要做的事
return ;//退出
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小))
{
处理节点;
DFS(路径,选择列表);
回溯:回到没用过
}
return ;//退出
}
五、例题分析
组合问题
题干描述
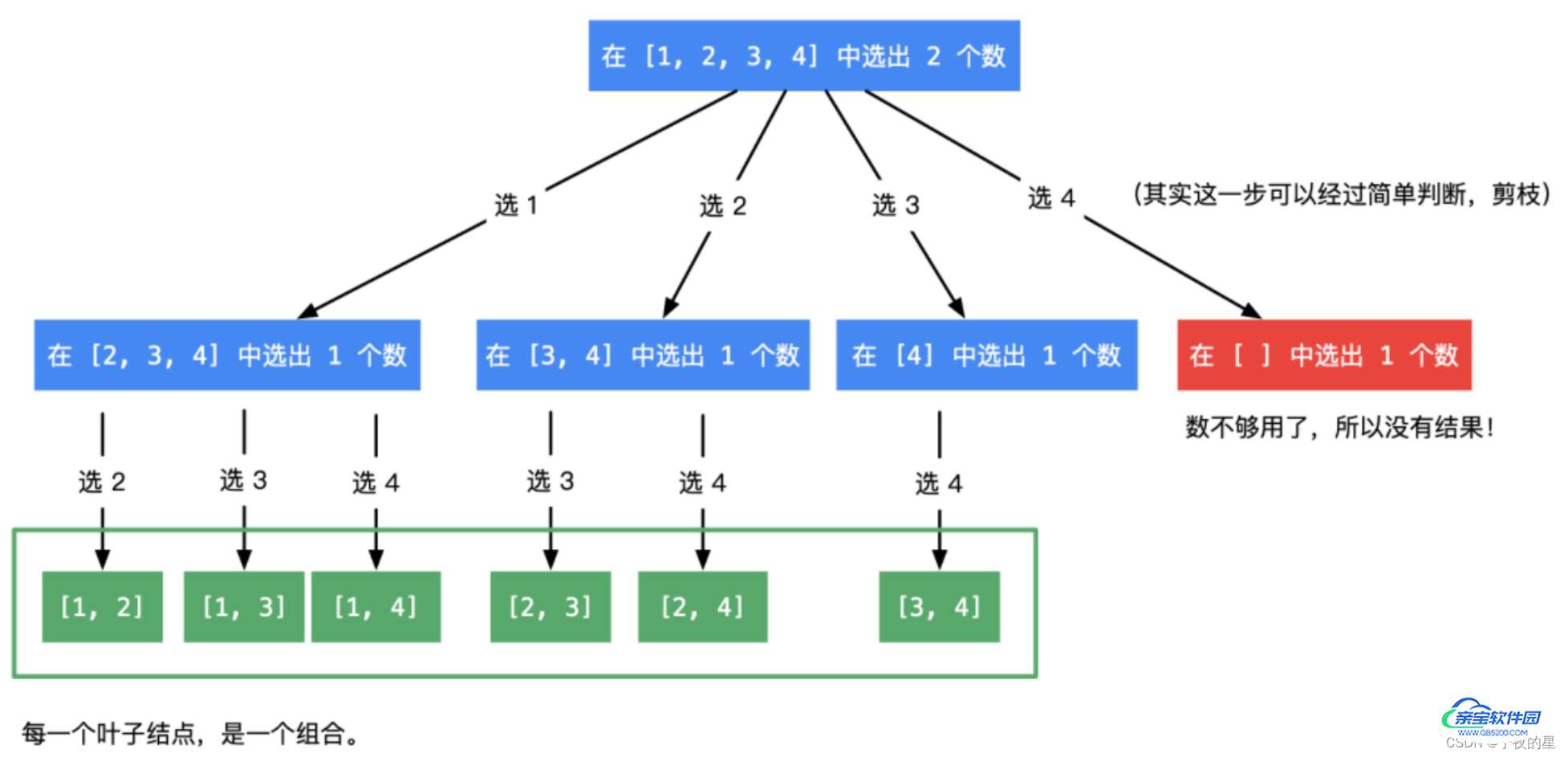
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
输入:n = 1, k = 1
输出:
[[1]]
思路分析
C语言代码:
int* path;
int pathTop;
int** ans;
int ansTop;
void DFS(int n, int k,int startIndex) {
//当path中元素个数为k个时,我们需要将path数组放入ans二维数组中
if(pathTop == k) {
//path数组为我们动态申请,若直接将其地址放入二维数组,path数组中的值会随着我们回溯而逐渐变化
//因此创建新的数组存储path中的值
int* temp = (int*)malloc(sizeof(int) * k);
int i;
for(i = 0; i < k; i++) {
temp[i] = path[i];
}
ans[ansTop++] = temp;
return ;
}
int j;
for(j = startIndex; j <=n ;j++) {
//将当前结点放入path数组
path[pathTop++] = j;
//进行递归
DFS(n, k, j + 1);
//进行回溯,将数组最上层结点弹出
pathTop--;
}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
//path数组存储符合条件的结果
path = (int*)malloc(sizeof(int) * k);
//ans二维数组存储符合条件的结果数组的集合。(数组足够大,避免极端情况)
ans = (int**)malloc(sizeof(int*) * 10000);
pathTop = ansTop = 0;
DFS(n, k, 1);
//最后的返回大小为ans数组大小
*returnSize = ansTop;
//returnColumnSizes数组存储ans二维数组对应下标中一维数组的长度(都为k)
*returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
int i;
for(i = 0; i < *returnSize; i++) {
(*returnColumnSizes)[i] = k;
}
//返回ans二维数组
return ans;
}
加载全部内容