JavaScript遍历实现DFS算法和BFS算法

时间:2023-02-03 itwangyang 人气:0

DFS(Depth first search)

Depth first search 称作「深度优先遍历」

下面结合具体例子来理解。如图所示，在一个九宫格图中，绿色位置代表起始位置，红色代表终点位置，灰色区域和宫格图的边界代表此路不通，请从起始位置按照每次只能移动一格的方法移动到终点位置。

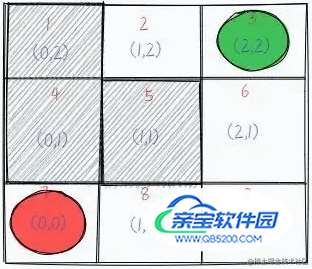
我们用 DFS 的方法去解这道题，由图可知，我们可以走上下左右四个方向，我们不妨先约定 “左>上>右>下” 的顺序走，即，如果左边可以走，我们先走左边。然后「递归」下去，没达到终点，我们再原路返回，等又返回到这个位置时，左边已经走过了，那么我们就走上面，按照这样的顺序走。并且我们把走过的路（方向）作标记表示“不能走回头路”。

按照约定，我们先从起点首先向左走到位置 2，这时发现左边不能走了，这时我们就考虑往上走，发现也不能走，同理，下边也不能走。右边刚才已经走过了也不能走，这时候无路可走了，代表这条路不能通往终点，所以现在「无路可走」的时候，沿着原路返回，直到回到了还有未走过的路的路口，尝试继续走没有走过的路径。

于是我们只有回到最初的位置 1，然后判断左边刚才已经走过了并且证实这个方向行不通，那就不必走了，上和右也是不通，所以我们走下边。于是走到了 6 的位置，此时还是按照约定“左>上>右>下” 的顺序走，左边和右边依然不通，上边刚才已经走过了，所以得继续往下走。

继续往下那就是位置 9 了，到了这个路口我们继续按照约定“左>上>右>下” 的顺序，先往左发现可以走，那么就继续走到位置 8，到了位置 8 还是按照刚才的思路继续往左，发现还可以走，并且最终到达终点位置 7。

综上所述，这个过程就是「深度优先遍历」。

DFS 的重点在于状态回溯，因此我们作个思路总结：

深度优先遍历 只要前面有可以走的路，就会一直向前走，直到无路可走才会回头；
「无路可走」有两种情况：① 遇到了墙；② 遇到了已经走过的路；
在「无路可走」的时候，沿着原路返回，直到回到了还有未走过的路的路口，尝试继续走没有走过的路径；
有一些路径没有走到，这是因为找到了出口，程序就停止了；
「深度优先遍历」也叫「深度优先搜索」，遍历是行为的描述，搜索是目的（用途）；
遍历不是很深奥的事情，把所有可能的情况都看一遍，才能说「找到了目标元素」或者「没找到目标元素」。遍历也称为穷举，穷举的思想在人类看来虽然很不起眼，但借助计算机强大的计算能力，穷举可以帮助我们解决很多专业领域知识不能解决的问题。

使用 DFS 来解答刚才题目的代码如下：

//我们以红点位置为坐标{0,0}，绿色位置坐标为{2,2}
//目标的坐标位置
let target = {
  x: 0,
  y: 0
};
//绿色起点的坐标位置
let currentLocation = {
  x: 2,
  y: 2
};
let used = []; //用来标记地图上哪些点是走过的
let reached = false; //是否能到达目标位置
// 表示灰色区域的格子
const illegalLocation = [
  { x: 0, y: 2 }, //序号1的坐标
  { x: 0, y: 1 }, //序号4的坐标
  { x: 1, y: 1 } //序号5的坐标
];

function isLegalLocation({ x, y }, illegalLocation) {
  let flag = true;
  //位置不能在地图坐标之外
  if (x < 0 || x > 2 || y < 0 || y > 2) {
    return (flag = false);
  }
  //不能走的路径
  for (const { x: locX, y: locY } of illegalLocation) {
    if (x === locX && y === locY) {
      flag = false;
    }
  }
  return flag;
}

//向左移动
function toLeft({ x, y }) {
  return { x: x - 1, y };
}

//向上移动
function toTop({ x, y }) {
  return { x, y: y + 1 };
}

//向右移动
function toRight({ x, y }) {
  return { x: x + 1, y };
}

//向下移动
function toBottom({ x, y }) {
  return { x, y: y - 1 };
}

function dfs(target, location, illegalLocation, used) {
  // 如果当前位置与目标坐标相同表示可以抵达
  if (Object.entries(target).toString() === Object.entries(location).toString()) {
    console.log('reached', location);
    return (reached = true);
  }
  let current = location;
  const newIllegalLocation = illegalLocation.concat(used);
  //假设按照“左>上>右>下”的顺序走
  if (isLegalLocation(toLeft(location), newIllegalLocation)) {
    current = toLeft(location);
  } else if (isLegalLocation(toTop(location), newIllegalLocation)) {
    current = toTop(location);
  } else if (isLegalLocation(toRight(location), newIllegalLocation)) {
    current = toRight(location);
  } else if (isLegalLocation(toBottom(location), newIllegalLocation)) {
    current = toBottom(location);
  } else {
     //走不通了就直接返回
    return false
  }
  used.push(current); //将刚才走过的格子标记为已走过
  return dfs(target, current, illegalLocation, used); //递归下去
}

dfs(target, currentLocation, illegalLocation, used);

BFS(Breadth first search)

Breadth first search 称作「广度优先遍历」

BFS 较之 DFS 之不同在于，BFS 旨在面临一个路口时，把所有的岔路口都记下来，然后选择其中一个进入，然后将它的分路情况记录下来，然后再返回来进入另外一个岔路，并重复这样的操作，用图形来表示则是这样的：

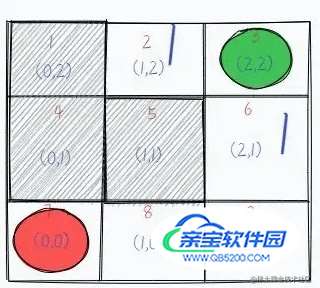
从绿色起点出发，记录所有的岔路口，并标记为走一步可以到达的。然后选择其中一个方向走进去，我们走绿色左边（序号为 2）的那个格子，然后将这个路口可走的方向记录下来并标记为 2，意味走两步可以到达的地方。

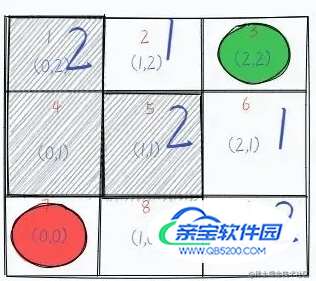
接下来，我们回到起点下面 1 的方块上（序号为 6），并将它能走的方向也记录下来，同样标记为 2，因为也是走两步便可到达的地方。这样走一步以及走两步可以到达的地方都搜索完毕了，后续同理，我们可以把走三步的格子给标记出来。

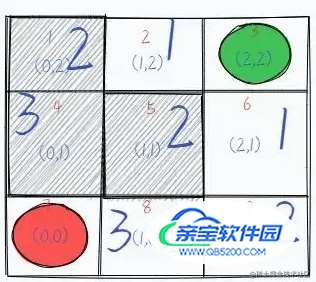
再之后是第四步。我们便成功寻找到了路径，并且把所有可行的路径都求出来了。

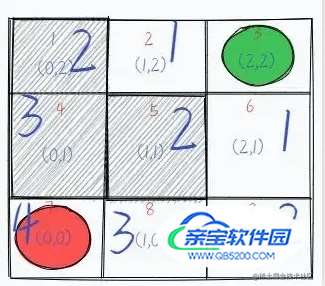
注意：格子序号分别为 1、4、5 的地方是灰色区域表示此路不通。

使用 BFS 来解答刚才题目的代码如下：

//我们以红点位置为坐标{0,0}，绿色位置坐标为{2,2}
//目标的坐标位置
let target = {
  x: 0,
  y: 0
};
//绿色起点的坐标位置
let currentLocation = {
  x: 2,
  y: 2
};
// 表示灰色区域的格子
const illegalLocation = [
  { x: 0, y: 2 }, //序号1的坐标
  { x: 0, y: 1 }, //序号4的坐标
  { x: 1, y: 1 } //序号5的坐标
];

function isLegalLocation({ x, y }, illegalLocation) {
  let flag = true;
  //位置不能在地图坐标之外
  if (x < 0 || x > 2 || y < 0 || y > 2) {
    return (flag = false);
  }
  //不能走的路径
  for (const { x: locX, y: locY } of illegalLocation) {
    if (x === locX && y === locY) {
      flag = false;
    }
  }
  return flag;
}

//向左移动
function toLeft({ x, y }) {
  return { x: x - 1, y };
}

//向上移动
function toTop({ x, y }) {
  return { x, y: y + 1 };
}

//向右移动
function toRight({ x, y }) {
  return { x: x + 1, y };
}

//向下移动
function toBottom({ x, y }) {
  return { x, y: y - 1 };
}

function bfs(target, location, illegalLocation) {
  let reached = false; //是否能到达目标位置
  let stack = [];  
  let searched = new Set(); //已经走过的格子
  stack.push(location);
  while (stack.length) {
    let temp = stack.pop();
    const newIllegalLocation = illegalLocation.concat([...searched]);
    //假设按照“左>上>右>下”的顺序走
    if (isLegalLocation(toLeft(temp), newIllegalLocation)) {
      temp = toLeft(temp);
    } else if (isLegalLocation(toTop(temp), newIllegalLocation)) {
      temp = toTop(temp);
    } else if (isLegalLocation(toRight(temp), newIllegalLocation)) {
      temp = toRight(temp);
    } else if (isLegalLocation(toBottom(temp), newIllegalLocation)) {
      temp = toBottom(temp);
    } else {
      //没有通路就直接返回
      return false
    }
    searched.add(temp);
    stack.push(temp);
    for (const { x: locX, y: locY } of searched) {
      if (target.x === locX && target.y === locY) {
        //如果当前位置与目标坐标相同表示可以抵达
        reached = true;
        console.log('reached: ', reached);
        stack = [];
        break;
      }
    }
  }
  return reached;
}
bfs(target, currentLocation, illegalLocation);

「广度优先遍历」的思想在生活中随处可见：

如果我们要找一个律师，我们会先在朋友中查找，如果没有找到，继续在朋友的朋友中查找，直到找到为止。
把一块石头投入平静的水面，激起的一层一层波纹就呈现「广度优先遍历」的特点。

总结

「一条路走到底，不撞南墙不回头」是对 DFS 的最直观描述。因此 DFS 可以借助「递归」实现。
BFS 呈现出「一层一层向外扩张」的特点，先看到的节点先遍历，后看到的节点后遍历，因此 BFS 可以借助「队列」实现。（遍历到一个节点时，如果这个节点有左（右）孩子节点，依次将它们加入队列。）
DFS 适合目标明确的寻找，而 BFS 适合大范围的寻找。

加载全部内容