JS快速检索碰撞图形之四叉树碰撞检测

时间:2023-02-03 前端西瓜哥人气:0

正文

在上篇文章我们讨论了使用 脏矩形渲染，通过重渲染局部的图形来提优化 Canvas 的性能，将 GPU 密集转换为 CPU 密集。

看这篇文章《Canvas 性能优化：脏矩形渲染》

CPU 密集在哪？

在需要遍历 所有的图形，判断它们是否和脏矩形发生相交（碰撞），保存发生碰抓给你的图形，将它们在局部进行重绘。

有没有办法减少需要遍历的图形，不要遍历全部的图形，而是少量的图形呢？有一个办法是使用 四叉树。

四叉树碰撞检测原理

我们将区域的分割表述为 “节点”，因为是四叉树；

将画布上的真实图形就叫做 “图形”。

四叉树本质使用了 空间分割，给图形加索引，将视口界面分割成多个区域，每个区域记住自己包含了哪些图形。

然后移动目标图形时，判断它落在哪个区域，取出所在区域的图形，这些图形集合就是和目标图形发生碰撞图形的超集。

这些区域外的图形就被我们排除了。

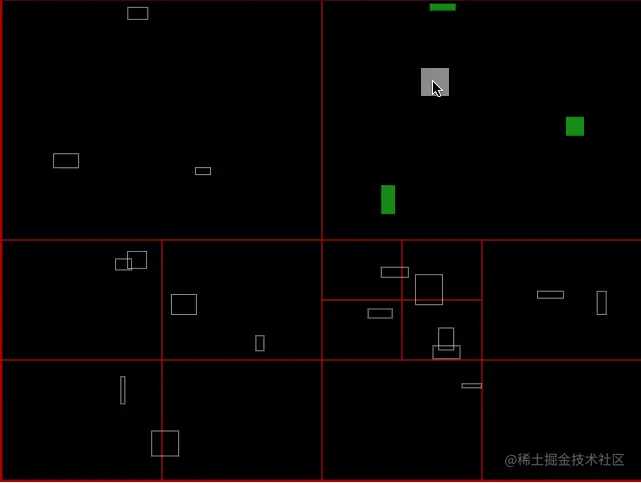
算法实现的要点：

创建根节点，根节点保存区域的信息 x、y、width 和 height。

添加图形时，当一个节点内的节点数量大于阀值，就将整个区域均等切割为 4 等份的子节点，将图形从当前区域取出，重新放入到这些子节点内，从而将节点的归属划分为更小的区域。

（原来的区域转换为索引层，真正保存节点的地方放到了它的子区域上）

当我们提供一个碰撞矩形，我们从四叉树顶节点往下找，看是否有子节点。如果有，使用矩形碰撞算法找出它所在的子节点有哪些（可能有多个）。对这些子节点重复前面的操作，进行递归，找到所有的图形。

这些图形就是碰撞矩形可能相交的矩形，但相对所有图形，又不至于太多。

四叉树碰撞检测算法

先看看经典算法实现。

算法我就不自己实现了，这里展示 quadtree-js 库的代码实现。

github.com/timohausman…

构造函数：

function Quadtree(bounds, max_objects, max_levels, level) {
  this.max_objects = max_objects || 10; // 节点内最大对象数量
  this.max_levels = max_levels || 4; // 树的最大深度
  this.level = level || 0;
  this.bounds = bounds; // 区域，结构为 {x, y, width, height}
  this.objects = []; // 保存图形的地方
  this.nodes = []; // 4 个子节点，到达阀值时才创建
}

这是一个内部私有方法，当节点内图形过多，超过阀值，就将当前节点分裂成 4 个子节点：

// 切割：生成 4 个子节点
Quadtree.prototype.split = function () {
  var nextLevel = this.level + 1,
    subWidth = this.bounds.width / 2,
    subHeight = this.bounds.height / 2,
    x = this.bounds.x,
    y = this.bounds.y;
  // 右上
  this.nodes[0] = new Quadtree(
    {
      x: x + subWidth,
      y: y,
      width: subWidth,
      height: subHeight,
    },
    this.max_objects,
    this.max_levels,
    nextLevel
  );
  // 左上
  this.nodes[1] = new Quadtree(
    {
      x: x,
      y: y,
      width: subWidth,
      height: subHeight,
    },
    this.max_objects,
    this.max_levels,
    nextLevel
  );
  // 左下
  this.nodes[2] = new Quadtree(
    {
      x: x,
      y: y + subHeight,
      width: subWidth,
      height: subHeight,
    },
    this.max_objects,
    this.max_levels,
    nextLevel
  );
  // 右下
  this.nodes[3] = new Quadtree(
    {
      x: x + subWidth,
      y: y + subHeight,
      width: subWidth,
      height: subHeight,
    },
    this.max_objects,
    this.max_levels,
    nextLevel
  );
};

计算某个图形落在当前节点的哪个子节点，拿到对应节点索引值数组：

// 找到某个 box 落在在哪个区域
Quadtree.prototype.getIndex = function (pRect) {
  var indexes = [],
    verticalMidpoint = this.bounds.x + this.bounds.width / 2,
    horizontalMidpoint = this.bounds.y + this.bounds.height / 2;
  var startIsNorth = pRect.y < horizontalMidpoint,
    startIsWest = pRect.x < verticalMidpoint,
    endIsEast = pRect.x + pRect.width > verticalMidpoint,
    endIsSouth = pRect.y + pRect.height > horizontalMidpoint;
  // top-right quad
  if (startIsNorth && endIsEast) {
    indexes.push(0);
  }
  // top-left quad
  if (startIsWest && startIsNorth) {
    indexes.push(1);
  }
  // bottom-left quad
  if (startIsWest && endIsSouth) {
    indexes.push(2);
  }
  // bottom-right quad
  if (endIsEast && endIsSouth) {
    indexes.push(3);
  }
  return indexes;
};

插入一个图形，先看是否存在子节点，有的话说明当前节点变成了索引层，通过矩形碰撞算法找到所在的子节点，对这些子节点做插入操作：

Quadtree.prototype.insert = function (pRect) {
  var i = 0,
    indexes;
  // 存在子节点，则插入到子节点
  if (this.nodes.length) { 
    indexes = this.getIndex(pRect); // 找到索引位置
    for (i = 0; i < indexes.length; i++) {
      this.nodes[indexes[i]].insert(pRect); // 递归 insert
    }
    return;
  }
  // 没有子节点，不是索引层，图形放到前节点下
  // （有个小 BUG，就是不在范围内的图形也加上去了）
  this.objects.push(pRect);
  // 如果对象太多，构建子节点
  if (
    this.objects.length > this.max_objects &&
    this.level < this.max_levels
  ) {
    if (!this.nodes.length) {
      this.split();
    }
    // 将 objects 取出，放入这些子节点中
    for (i = 0; i < this.objects.length; i++) {
      indexes = this.getIndex(this.objects[i]);
      for (var k = 0; k < indexes.length; k++) {
        this.nodes[indexes[k]].insert(this.objects[i]);
      }
    }
    this.objects = [];
  }
};

返回目标图形所在节点下的所有图形：

// 传入一个矩形，取出它所在节点的所有矩形
// 这个方法能返回
Quadtree.prototype.retrieve = function (pRect) {
  // 提取目标矩形所在区间下的所有矩形
  var indexes = this.getIndex(pRect),
    returnObjects = this.objects;
  // 可能需要递归。
  //if we have subnodes, retrieve their objects
  if (this.nodes.length) {
    for (var i = 0; i < indexes.length; i++) {
      returnObjects = returnObjects.concat(
        this.nodes[indexes[i]].retrieve(pRect)
      );
    }
  }
  // 移除重复的节点
  returnObjects = returnObjects.filter(function (item, index) {
    return returnObjects.indexOf(item) >= index;
  });
  return returnObjects;
};

非常简单，一些可以改善的能力。

没有添加映射功能，最后返回的图形都是 box 对象信息，我们可以考虑改造为 insert(rect, data)，保存额外的信息，比如实际形状对象或 id。
动态收缩：移除某个图形后更新树结构，并在发现图形数量低于阀值时，取出图形放到父节点上，销毁子节点；
修改根节点范围 后，需要重置整棵树，如何高效重置等；
四叉树的图形类型，常见的是矩形，但还可以是点、直线、曲线等，如果需要可以考虑支持。

请根据实际需要进行扩展。

一些权衡

处于节点内分割线上的图形，它是归属于多个子节点的，所以最终会同时放到它的多个子节点下，会花费内存。

极端情况下，一个非常大的图形，会保存在所有的节点下。

如果想节省内存，可以直接保存到当前节点上，不放到子节点上，可以减少内存使用，只是最后返回的被碰撞图形会多一点。因为图形可能只压在了两个子节点的交界线上，比如 A、 B ，但目标矩形是在其他的子节点 C 上，但因为它们来自同一个父节点，所以拿到了这个不可能在 C 的图形。

后者会更好一些，但如果一个图形刚好在画布中心，那每次取出的碰撞图形都会有它（这点可以通过松散四叉树解决）。

松散四叉树

经典四叉树有个问题，就是如果图形的物理信息是比较动态的，当总是在边界附近时，就会发生频繁地将图形从一个节点取出并放到另个节点下。

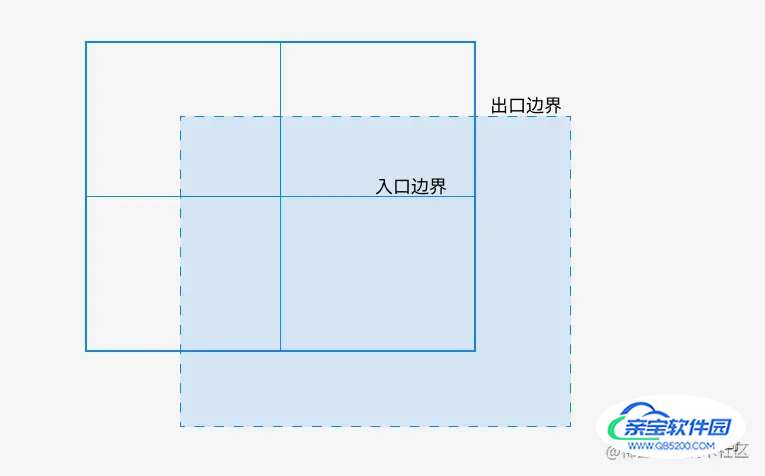
对此我们可以额外设置一个出口边界。这个出口边界要比入口边界要大，只有当图形离开这个出口边界，才会更新提取图形到新的节点。

这样，当图形划分到另一个节点上时，就 需要移动较长的距离才能回到原来节点下，轻微地移动不会导致剧烈的更新。

通常出口边界边长为入口边界的两倍最佳，为什么不知道，经验之谈。

其他空间分割思想的算法

简单介绍一些也使用了 空间分割 思想的算法。

跳表：一种有序链表，通过叠加大量的索引层，可以进行链表形式的 “二分查找”，达到高效的 O(logn) 时间复杂度，但也带来了内存的消耗。Redis 中的有序集合（Sorted Set）底层使用了跳表，一个原因是可以高效地获取区间内的数据集；
B+ 树：一种平衡二叉树，有点像跳表，但树的层数最多为三层，MySQL 的索引实现使用了 B+ 树，因为层数较少，可以减少 IO 操作；
R 树：R 表示矩形的意思。相比前面两种单维的范围查找，R 树能做高效的高维查找。比如地图中，我们可以通过 R 树将距离相近的高维图形合并为一个大节点，当搜索 “2km 内的药店” 时，如果你落到某个大节点上，我们只要遍历一个大节点下的所有节点，而不是遍历整个市，或整个国家。

R 树的思路是最接近四叉树的，它其实是另一种减少图形遍历的方案，可以适用于高效剔除视口范围之外的图形。

R 树有个 star 数很多的库，叫做 RBush，感兴趣可以看看。

github.com/mourner/rbu…

加载全部内容