Python关于维卷积的理解

时间:2023-02-03 静静喜欢大白人气:0

关于维卷积的理解

功能

一维卷积一般用于处理文本数据，常用语自然语言处理中，输入一般是文本经过embedding的二维数据。

定义

tf.layers.conv1d(
inputs,
filters,
kernel_size,
strides=1,
padding='valid',
data_format='channels_last',
dilation_rate=1,
activation=None,
use_bias=True,
kernel_initializer=None,
bias_initializer=tf.zeros_initializer(),
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
bias_constraint=None,
trainable=True,
name=None,
reuse=None
)

参数

重要参数介绍：

inputs：输入tensor，维度(batch_size, seq_length, embedding_dim) 是一个三维的tensor；其中，batch_size指每次输入的文本数量；seq_length指每个文本的词语数或者单字数；embedding_dim指每个词语或者每个字的向量长度；例如每次训练输入2篇文本，每篇文本有100个词，每个词的向量长度为20，那input维度即为(2, 100, 20)。
filters：过滤器（卷积核）的数目
kernel_size：卷积核的大小，卷积核本身应该是二维的，这里只需要指定一维，因为第二个维度即长度与词向量的长度一致，卷积核只能从上往下走，不能从左往右走，即只能按照文本中词的顺序，也是列的顺序。

举例

代码

# coding: utf-8
import tensorflow as tf
 
num_filters = 2
kernel_size = 2
batch_size = 1
seq_length = 4
embedding_dim = 5
 
embedding_inputs = tf.constant(-1.0, shape=[batch_size, seq_length, embedding_dim], dtype=tf.float32)
 
with tf.name_scope("cnn"):
    conv = tf.layers.conv1d(embedding_inputs, num_filters, kernel_size, name='conv')
 
session = tf.Session()
session.run(tf.global_variables_initializer())
 
print (session.run(conv).shape)

输出为(1, 3, 2)。

原理

首先，batch_size = 1即为一篇文本，seq_length = 4定义文本中有4个字（假设以字为单位），embedding_dim = 5定义一个字的向量长度为5，这里初始化每个字的向量都为[1, 1, 1, 1, 1]，num_filters = 2定义有两个过滤器，kernel_size = 2定义每个卷积核的宽度为2，长度即为字向量长度5。

一个卷积核通过卷积操作之后得到(4-2+1)*1（seq_length - kernel_size + 1）即3*1的向量，一共有两个卷积核，所以卷积出来的数据维度(1, 3, 2)其中1指一篇文本。

图解

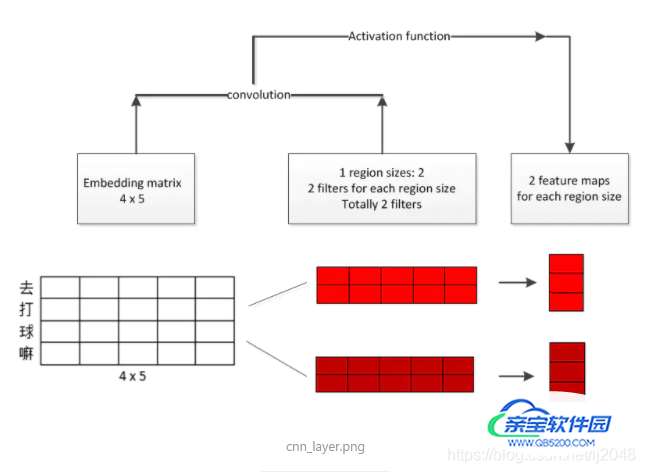
后续

经过卷积之后得到2个feature maps，分别经过pooling层之后，两个3*1的向量就变成两个1*1的常数，在把这两个1*1的常数拼接在一起变成2*1向量，之后就可以进行下一步比如全连接或者softmax操作了。

Python编写一维数组的卷积

之前在网上查阅关于数组卷积的代码时，发现有很多C++代码，但并没有多少关于python的代码，故在此将自己所编写的代码分享出来，希望能一起探讨研究。

实现思路如下

1、先将短数组反转

2、第一阶段，此时只有短数据的（前）部分元素与长数据相乘求和

3、第二阶段，此时短数据的所有元素与长数据相乘求和

4、第三阶段，此时短数据的（后）部分数据与长数据相乘求和

具体应用公式网上有很多，计算过程并不复杂，但比较麻烦的是关于循环变量的边界值的设置，稍有不慎就有可能超出索引值。我的办法是先在草稿纸上写两个数组，元素可以少取几个，然后写出具体卷积的过程数据，尤其不同阶段的过渡的位置，细心找出规律，然后就可以编写具体代码了。

代码入下：

    import matplotlib.pyplot as plt
    import numpy as np

#阶跃信号
def up(x):
    for i in range(len(x)):
        if x[i] < 0:
            y[i] = 0
        else:
            y[i] = 1
    return y

x= np.arange(-10,10,0.1)
y = np.zeros(len(x))

y = up(x)

plt.plot(y)
plt.show()



#高斯滤波器
def gauss(x,s):
    
    g=1/(((2*np.pi)**0.5)*s)*np.exp(-x**2/2/(s**2))
    return g

sample = np.arange(-10,10,1)
g = gauss(sample,10/3)

plt.plot(g)
plt.show()

#卷积一
f_1 = np.zeros(len(y)+len(g)-1)

#翻转
g = list(g)
g.reverse()

for i in range(len(f_1)):
    #长数据卷积部分短数据（前半部分）
    if i < (len(g)-1):
        for j in range(i+1):
            f_1[i] = y[j]*g[i-j]+f_1[i]
    #长数据卷积整个短数据
    elif i < (len(y)-1):
        for j in range(i-len(g)+1,i+1):
            f_1[i] = y[j]*g[i-j]+f_1[i]
    #长数据卷积部分短数据（后半部分）
    else:
        for j in range(i-len(g)+1,len(y)):
            f[i] = y[j]*g[i-j]+f[i]
           
               

            
#显示
plt.plot(f_1)
plt.show()


#卷积二

#存放卷积后的结果
f_2 = np.zeros(len(y)+len(g)-1)

#翻转
g = list(g)
g.reverse()

for i in range(len(f_2)):
    
    #根据卷积的不同阶段设置阈值
    t_left = i-len(g)+1
    t_right = i+1
    
    #卷积的前半部分j的初始值
    if t_left < 0:
        t_left = 0
    #卷积的后半部分j的上限
    if t_right > len(y):
        t_right = len(y)
    
    for j in range(t_left,t_right):

        f_2[i] = y[j]*g[i-j] + f_2[i]

#显示        
plt.plot(f_2)
plt.show()

两种设置阈值的方式，但思想都是一样的。

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持。

加载全部内容