Java排序之冒泡排序的实现与优化
指北君 人气:1jwt简介
冒泡排序:(Bubble Sort)是一种简单的交换排序。之所以叫做冒泡排序,因为我们可以把每个元素当成一个小气泡,根据气泡大小,一步一步移动到队伍的一端,最后形成一定对的顺序。
冒泡排序的原理
我们以一个队伍站队为例,教官第一次给队员排队是无序的,这时候就需要排队,按矮到高的顺序排列,首先拎出第一第二个比较,如果第一个队员比第二个要高,则两个交换位置, 高的放到排到第二个位置,矮的就排到第一个,再把第二个,第三个比较,把高的排到后面一个位置,然后以此类推,直至第一轮所有队员都比较过一次(记住每次比较都是相邻的两个),这样就可以把最高的排到最后的位置。
总结就是: 每一轮都需要从第一位开始进行相邻的两个数的比较,将较大的数放后面,比较完毕之后向后挪一位继续比较下面两个相邻的两个数大小关系,重复此步骤,直到最后一个还没归位的数。
冒泡排序流程图
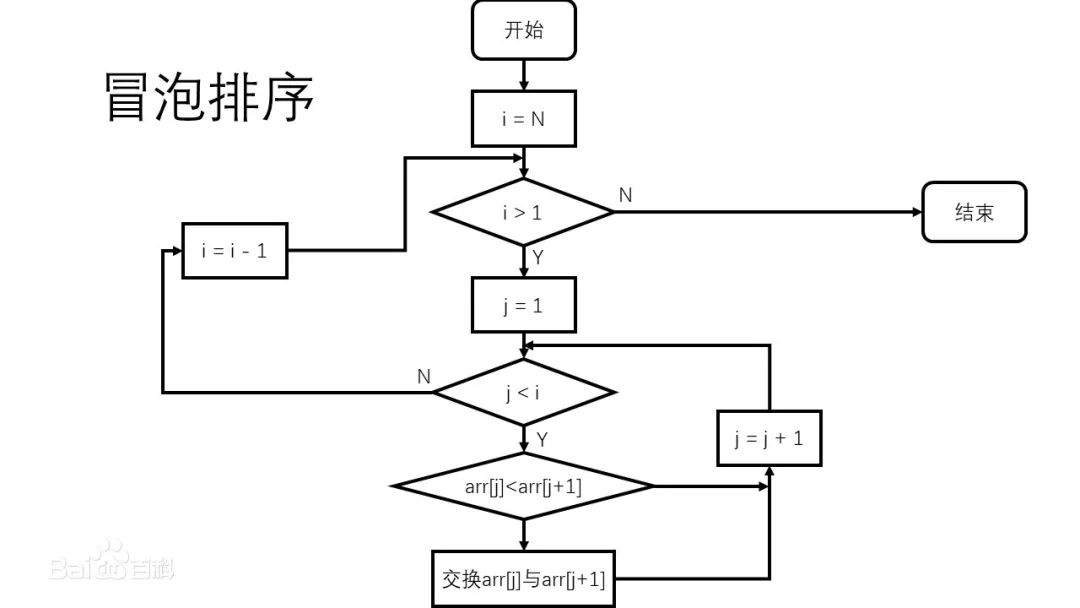
我们进行分解看看每一步是怎么执行的
首先我们给个无序数组 [3,14,32,16,53,8] 进行升序排序
第一轮:初始值 [3,14,32,16,53,8]

如图所示,走完第一轮之后,我们得到的结果就是[3,14,16,32,8,53],此时已经将最大的数53排到了指定位置,所以冒泡排序每一轮只能确定将一个数归位。即第一趟只能确定将末位上的数归位, 第二趟只能将倒数第 2 位上的数归位,依次类推下去
第二轮:初始值 [3,14,16,32,8,53]
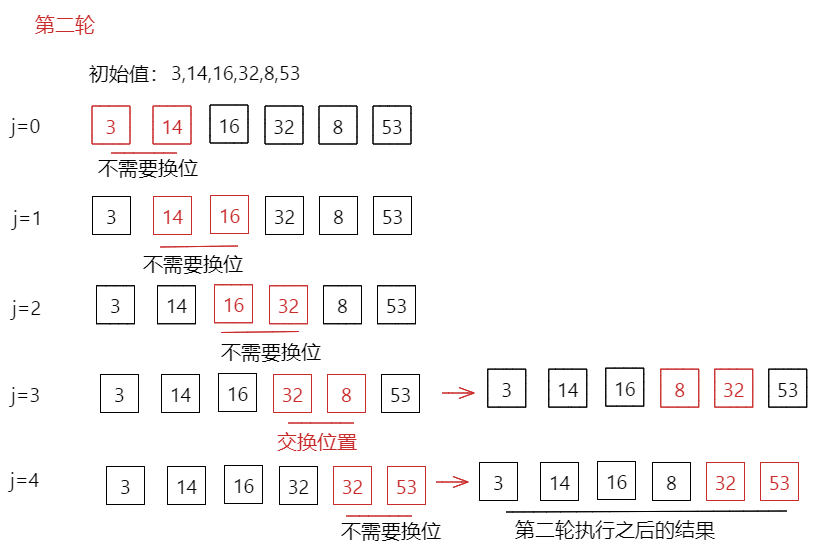
第二轮排序结果[3,14,16,8,32,53]
第三轮:初始值 [3,14,16,8,32,53]
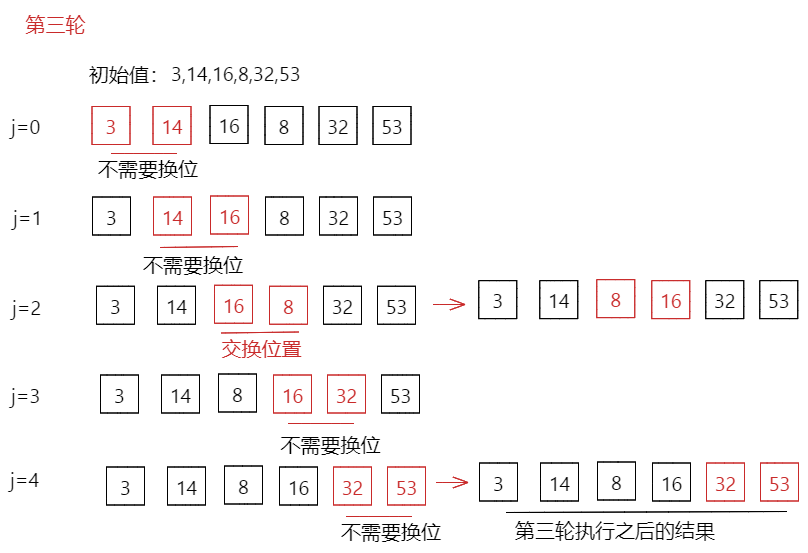
第三轮排序结果[3,14,8,16,32,53]
第四轮:初始值 [3,14,8,16,32,53]

第四轮排序结果[3,8,14,16,32,53]
第五轮:初始值 [3,8,14,16,32,53]
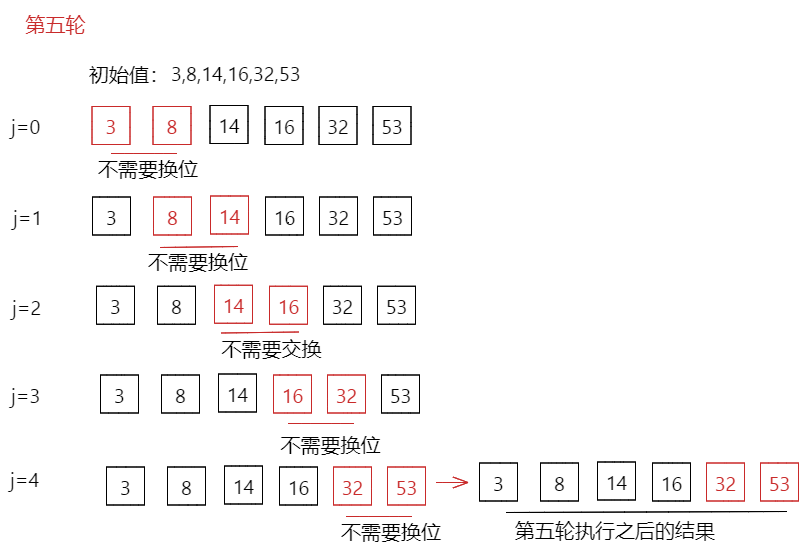
第五轮排序结果[3,8,14,16,32,53] 到这,我们最终排序完成。
Java代码实现
public static void bubbleSort(int[] array){
for(int i=0;i<array.length-1;i++){//控制比较轮次,一共 n-1 趟
int num = 0; //用来记录比每轮比较的次数
for(int j=0;j<array.length-1;j++){//控制两个挨着的元素进行比较
if(array[j] > array[j+1]){
//换位
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
//比较一次,加1
num =num+1;
}
//结果输出
System.out.print("第"+(i+1)+"轮:[");
for (int a=0;a<array.length; a++){
if(a!=array.length-1)
{
System.out.print(array[a]+",");
}else{
System.out.print(array[a]+"]");
}
}
System.out.println(",比较了:"+num+" 次");
}
}
输出结果
第1轮结果:[3,14,16,32,8,53],每轮比较了:5 次
第2轮结果:[3,14,16,8,32,53],每轮比较了:5 次
第3轮结果:[3,14,8,16,32,53],每轮比较了:5 次
第4轮结果:[3,8,14,16,32,53],每轮比较了:5 次
第5轮结果:[3,8,14,16,32,53],每轮比较了:5 次
我在每轮比较的时候定义了一个num来记录比较次数,大家可以看到长度为6的数组比较,比较了5轮,每轮都比较了5次, 但是通过上面拆分的每一轮比较细节可以看出,其实约到后面的比较,有一部分已经是排好了,如果某个数比他的下一个位置还小, 就没有必要和后面已经排好的数据再做比较,这样只会增加程序运行压力。
比如,第四轮,8和14比较,换位之后,16,32,53都已经排好了,14再和16比较,不用换位,那16之后的数据已经在第三轮排好,就没必要再比较16和32,32和53了。
那我们来对程序做一个优化,其实在第一轮把最大的数字排到最后之后,第二轮就不用再和最后一个数字比较,因为最大的数字已经排好,再比较也只能排在最后一位之前了。
优化
我们就在程序内层循环做一个限制,每轮比较之后,下一轮就比较到array.length-1-i的位置。就是第一轮6位数都比较完成,最大排在最后,第二轮就比较前五个数,把前五个数中最大的排在第五位。这样以此类推,就可以减少程序中无用的比较。
优化代码如下:
public static void bubbleSort(int[] array){
for(int i=0;i<array.length-1;i++){//控制比较轮次,一共 n-1 趟
int num = 0; //用来记录比每轮比较的次数
//每一轮比较一次就排除最后一位,每轮的最后一位一定是这轮最大的,所以-i,
for(int j=0;j<array.length-1-i;j++){//控制两个挨着的元素进行比较
//换位
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
//比较一次,加1
num =num+1;
}
//结果输出
System.out.print("第"+(i+1)+"轮结果:[");
for (int a=0;a<array.length; a++){
if(a!=array.length-1)
{
System.out.print(array[a]+",");
}else{
System.out.print(array[a]+"]");
}
}
System.out.println(",每轮比较了:"+num+" 次");
}
}
我们再来看看结果:
第1轮结果:[3,14,16,32,8,53],每轮比较了:5 次
第2轮结果:[3,14,16,8,32,53],每轮比较了:4 次
第3轮结果:[3,14,8,16,32,53],每轮比较了:3 次
第4轮结果:[3,8,14,16,32,53],每轮比较了:2 次
第5轮结果:[3,8,14,16,32,53],每轮比较了:1 次
由此,我们可以看到,由之前30次比较减少到15次,所以程序压力会少很多,程序复杂度也降低了。由上面结果可知:6位长度的数组需要排五轮,每轮次数减1,那如果由n个长度的数组,需要比较多少次呢?
- 第一轮:6-1
- 第二轮:6-2
- 第三轮:6-3
- 倒数第二轮:2
- 倒数第一轮:1
得出结果:(n-1)+(n-2)+...+2+1 = n(n-1)/2 =1/2n^2 -1/2n
是一个等差数列,按照时间复杂度规则,直接取最高阶项并去除常熟系数等到时间复杂度就是 O(n^2)了
到这,我们的冒泡排序就了解完了。
加载全部内容