Python二叉树遍历

Python3中二叉树前序遍历的迭代解决方案

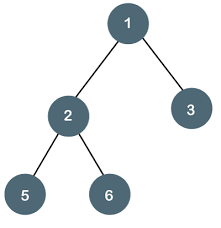
A Binary Tree

二叉树是分层数据结构，其中每个父节点最多有 2 个子节点。在今天的文章中，我们将讨论一个在大量技术编码面试中出现的重要主题。

问题陈述 ： 鉴于 根 二叉树，返回 其节点值的前序遍历 . 提供迭代解决方案而不是递归解决方案。

解决方案：

预购遍历 在二叉树中按以下顺序发生：

• 先访问根
• 遍历左子树
• 遍历右子树

为了用迭代解决方案解决这个问题，我们必须实现 堆 数据结构。这是一种非线性数据结构，其中操作按 LIFO（后进先出）顺序执行。我们回答的方法很简单，如下所示：

• 我们将初始化两个列表 IE 一个承载输出，另一个充当我们的堆栈数据结构。堆栈将使用二叉树的根值进行初始化。
• 然后，只要堆栈有值，我们就会在堆栈上执行一个 while 循环。在循环中，依次进行以下操作：
• 删除（弹出）堆栈中最顶部的值（根节点）并将其附加到输出列表
• 将弹出值的右孩子压入堆栈
• 将弹出值的左孩子压入堆栈
• 返回循环结束时的输出列表

作为这个过程的结果，将首先访问根值，然后访问左子树，最后访问右子树值。

需要注意的是，右孩子首先被推入堆栈，然后是左孩子。这是因为堆栈的 LIFO 特性。这样做将允许我们先访问左孩子，然后再访问右孩子。

说话很便宜，给我看代码：

 # 二叉树节点的定义 类树节点：  
 def __init__(self, val=0, left=None, right=None):  
 自我.val = val  
 self.left = 左  
 self.right = 对 类解决方案：  
 def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:  
 输出，节点堆栈 = []，[根]  
          
 而节点堆栈：  
 节点 = nodestack.pop()  
 if node: # preorder: root -> left -> right  
 output.append(node.val)  
 nodestack.append(node.right)  
 nodestack.append(node.left)  
 返回输出

如果这篇文章对您有帮助，请随意喜欢并订阅我的时事通讯，以获取更多 Python 中的 DSA 内容。