Python数据结构树
Ding Jiaxiong 人气:01.示例
树的一些属性:
- 层次性:树是按层级构建的,越笼统就越靠近顶部,越具体则越靠近底部。
- 一个节点的所有子节点都与另一个节点的所有子节点无关。
- 叶子节点都是独一无二的。
- 嵌套
2.术语及定义
- 节点:树的基础部分。节点的名字 → 键,附加信息 → 有效载荷。
- 边:两个节点通过一条边相连,表示它们之间存在关系。除了根节点,其他每个结点都仅有一条入边,出边则可能有多条。
- 根节点:树中唯一没有入边的结点。
- 路径:由边连接的有序节点列表。
- 子节点:一个节点通过出边与子节点相连。
- 父节点:一个节点是其所有子节点的父节点。
- 兄弟节点:具有同一父节点的结点 → 互称兄弟节点。
- 子树:一个父节点及其所有后代的节点和边构成一棵子树。
- 叶子结点:叶子节点没有子节点。
- 层数:节点n的层数是从根节点到n的唯一路径长度。根节点的层数为0。
- 高度:树的高度是其中节点层数的最大值。
1.定义一:树由节点及连接节点的边构成。
树的属性:
- 有一个根节点除根节点外,其他每个节点都与其唯一的父节点相连。
- 从根节点到其他每个节点有且仅有一条路径。
- 如果每个节点最多有两个子节点 → 二叉树。
2.定义二:一棵树要么为空,要么由一个根节点和零棵或多棵子树构成,子树本身也是一棵树。
每棵子树的根节点通过一条边连到父树的根节点。
3.实现
3.1 列表之列表
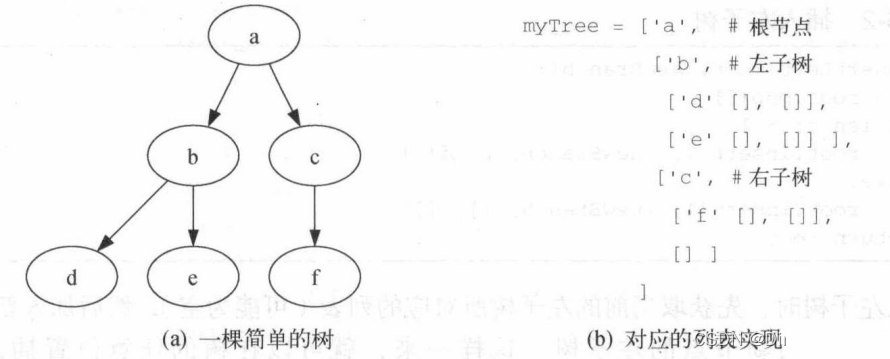
树的根节点是myTree[0],左子树是myTree[1],右子树是myTree[2]。
# 列表函数
def BinaryTree(r):
return [r,[],[]] # 根节点r,和两个作为子节点的空列表
# 插入左子树
def insertLeft(root,newBranch):
t = root.pop(1)
if len(t) > 1:
root.insert(1,[newBranch,t,[]])
else:
root.insert(1,[newBranch,[],[]])
return root
## 插入右子树
def insertRight(root , newBranch):
t = root.pop(2)
if len(t) > 1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2,[newBranch,[],[]])
return root
### 树的访问函数
def getRootVal(root):
return root[0]
def setRootVal(root,newVal):
root[0] = newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]
r = BinaryTree(3)
insertLeft(r,4)
print(r)3.2节点与引用
定义一个类,其中有根节点和左右子树的属性。
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
## 插入左子节点
def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.left = self.leftChild
self.leftChild = t
## 插入右子节点
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.right = self.rightChild
self.rightChild = t
## 访问函数
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self,obj):
self.key = obj
def getRootVal(self):
return self.key4.二叉树的应用
4.1解析树
- 根据完全括号表达式构建解析树
- 如何计算解析树中的表达式
- 如何将解析树还原成最初的数学表达式
解析树构建器:
import operator
from pythonds.basic import Stack
from pythonds.trees import BinaryTree
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree("")
pStack.push(eTree)
currentTree = eTree
for i in fplist:
if i == "(":
currentTree.insertLeft("")
pStack.push(currentTree)
currentTree = currentTree.getLeftChild()
elif i not in "+-*/)":
currentTree.setRootVal(eval(i))
parent = pStack.pop()
currentTree = parent
elif i in "+-*/":
currentTree.setRootVal(i)
currentTree.insertRight("")
currentTree = currentTree.getRightChild()
elif i == ")":
currentTree = pStack.pop()
else:
raise ValueError("Unkown Operator :" + i )
return eTree
## 计算二叉解析树的递归函数
def evaluate(parseTree):
opers = {
"+":operator.add,"-":operator.sub,
"*":operator.mul,"/":operator.truediv
}
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC:
fn = opers[parseTree.getRootVal()]
return fn(evaluate(leftC),evaluate(rightC))
else:
return parseTree.getRootVal()4.2树的遍历
- 前序遍历【根左右】
- 中序遍历【左根右】
- 后序遍历【左右根】
前序遍历算法实现为外部函数:
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild)前序遍历算法实现为BinaryTree类的方法
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()后序遍历函数
def postorder(tree):
if tree != None:
postorder(tree.getLeftChild())
postorder(tree.getRightChild())
print(tree.getRootVal())中序遍历函数
def inorder(tree):
if tree != None:
inorder(tree.getLeftChild())
print(tree.getRootVal())
inorder(tree.getRightChild())5.利用二叉堆实现优先级队列
队列一个重要的变体 → 优先级队列。和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的,优先级最高的元素在最前,最低的元素在最后。
实现优先级队列的经典方法 → 二叉堆。入队和出队操作均可达到O(logn)
- 最小堆【最小的元素一直在队首】
- 最大堆【最大的元素一直在队首】 6.6.2 二叉堆的实现
结构属性:
- 完全二叉树:除了最底层,其他每一层的节点都是满的。且在最底层,从左往右填充节点。
- 完全二叉树可以用一个列表直接表示。
堆的有序性:对于堆中任意元素x及其父元素p,p都不大于x。
堆操作
代码实现:
class EchaDui:
# 新建二叉堆
def __init__(self):
self.heapList = [0]
self.currentSize = 0
def percUp(self,i):
while i // 2 > 0:
if self.heapList[i] < self.heapList[i // 2]:
tmp = self.heapList[i // 2]
self.heapList[i // 2] = self.heapList[i]
self.heapList[i] = tmp
i = i // 2
# 新加元素
def insert(self,k):
self.heapList.append(k)
self.currentSize = self.currentSize + 1
self.percUp(self.currentSize)
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
def minChild(self,i):
if i * 2 + 1 > self.currentSize:
return i * 2
else:
if self.heapList[i*2] < self.heapList[i*2 + 1]:
return i * 2
else:
return i * 2 + 1
## 从二叉堆中删除最小的元素
def delMin(self):
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize = self.currentSize - 1
self.heapList.pop()
self.percDown(1)
return retval
## 根据元素列表构建堆
def builgHeap(self,alist):
i = len(alist) // 2
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
while (i > 0):
self.percDown(i)
i = i - 16.二叉搜索树
6.1搜索树的实现
二叉搜索树依赖性质:小于父节点的键都在左子树中,大于父节点的键则都在右子树。
代码实现:
class BinarySearchTree:
def __init__(self):
self.root = None
self.size = 0
def length(self):
return self.size
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
# 插入新节点
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root = TreeNode(key,val)
self.size = self.size + 1
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)
def __setitem__(self, key, value):
self._put(key,value)
## 查找键对应的值
def get(self,key):
if self.root:
res = self._get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key == key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def __getitem__(self, key):
return self.get(key)
# 检查树中是否有某个键
def __contains__(self, key):
if self._get(key,self.root):
return True
else:
return False
# 删除
def delete(self,key):
if self.size > 1:
nodeToRemove = self._get(key,self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size = self.size - 1
else:
raise KeyError("Error,key not in tree")
elif self.size == 1 and self.root.key == key:
self.root = None
self.size = self.size - 1
else:
raise KeyError("Error,key not in tree")
def __delitem__(self, key):
self.delete(key)
"""
1. 待删除节点没有子节点
2. 待删除节点只有一个子节点
3. 待删除节点有两个子节点
"""
# 寻找后继结点
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild.findMin()
else:
if self.parent:
if self.isLeftChild():
succ = self.parent
else:
self.parent.rightChild = None
succ = self.parent.findSuccessor()
self.parent.rightChild = self
return succ
def findMin(self):
current = self
while current.hasLeftChild():
current = current.leftChild
return current
def spliceOut(self):
if self.isLeaf():
if self.isLeftChild():
self.parent.leftChild = None
else:
self.parent.rightChild = None
elif self.hasAnyChildren():
if self.hasLeftChild():
if self.isLeftChild():
self.parent.leftChild = self.leftChild
else:
self.parent.rightChild = self.leftChild
self.leftChild.parent = self.parent
else:
if self.isLeftChild():
self.parent.leftChild = self.rightChild
else:
self.parent.rightChild = self.rightChild
self.rightChild.parent = self.parent
def remove(self,currentNode):
if currentNode.isLeaf():
if currentNode == currentNode.parent.leftChild:
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
elif currentNode.hasBothChildren():
succ = currentNode.findSuccessor()
succ.spliceOut()
currentNode.key = succ.key
currentNode.payload = succ.payload
else:
if currentNode.hasLeftChild():
if currentNode.isLeftChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else:
currentNode.replaceNodeData(currentNode.leftChild.key,
currentNode.leftChild.payload,
currentNode.leftChild.leftChild,
currentNode.leftChild.rightChild
)
else:
if currentNode.isLeftChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else:
currentNode.replaceNodeData(currentNode.rightChild.key,
currentNode.rightChild.payload,
currentNode.rightChild.leftChild,
currentNode.rightChild.rightChild
)
# 二叉搜索树迭代器
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChild:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
class TreeNode:
def __init__(self,key,val,left = None,right = None,parent = None):
self.key = key
self.payload = val
self.leftChild = left
self.rightChild = right
self.parent = parent
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = self7.平衡二叉搜索树(AVL树)
实现AVL树时,要记录每个节点的平衡因子。
平衡因子 = 左右子树的高度之差
→ 保证树的平衡因子为-1,0,1,可以使得关键操作获得更好的大O性能
#from 第6章树.二叉搜索树 import TreeNode
def _put(self, key, val, currentNode):
if key < currentNode.key:
if currentNode.hasLeftchi1d():
self._put(key, val, currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key, val,parent=currentNode)
self.updateBalance(currentNode.leftChild)
else:
if currentNode.hasRightChild():
self._put(key, val, currentNode.rightChild)
else:
currentNode.rightchild - TreeNode(key, val,parent=currentNode)
self.updateBalance(currentNode.rightChild)
def updateBalance(self, node):
if node.balanceFactor > 1 or node.balanceFactor < -1:
self.rebalance(node)
return
if node.parent != None:
if node.isLeftChild():
node.parent.balanceFactor += 1
elif node.isRightChild():
node.parent.balanceFactor -= 1
if node.parent.balanceFactor != 0:
self.updateBalance(node.parent)
# 实现左旋
def rotateLeft (self, rotRoot) :
newRoot = rotRoot .rightchild
rotRoot .rightChild = newRoot.leftChild
if newRoot . leftChild !=None :
newRoot . leftChild. parent = rotRoot
newRoot.parent =rotRoot.parent
if rotRoot .isRoot( ):
self.root = newRoot
else:
if rotRoot .isLeftChild():
rotRoot.parent .leftChild = newRoot
else:
rotRoot.parent .rightChild = newRoot
newRoot . leftChild = rotRoot
rotRoot.parent = newRoot
rotRoot. balanceFactor = rotRoot . balanceFactor + 1 - min(newRoot . balanceFactor,0)
newRoot . balanceFactor = newRoot . balanceFactor + 1 +max(rotRoot . balanceFactor,o )
# 实现再平衡
def rebalance(self, node) :
if node. balanceFactor < 0:
if node .rightChild .balanceFactor > 0:
self.rotateRight (node.rightChild)self.rotateLeft (node)
else:
self.rotateLeft (node)
elif node. balanceFactor > 0 :
if node . leftChild. balanceFactor < 0:
self.rotateLeft (node. leftChild)
self.rotateRight (node)
else:
self.rotateRight (node)
nceFactor + 1 - min(newRoot . balanceFactor,0)
newRoot . balanceFactor = newRoot . balanceFactor + 1 +max(rotRoot . balanceFactor,o )
# 实现再平衡
def rebalance(self, node) :
if node. balanceFactor < 0:
if node .rightChild .balanceFactor > 0:
self.rotateRight (node.rightChild)self.rotateLeft (node)
else:
self.rotateLeft (node)
elif node. balanceFactor > 0 :
if node . leftChild. balanceFactor < 0:
self.rotateLeft (node. leftChild)
self.rotateRight (node)
else:
self.rotateRight (node)加载全部内容