python matplotlib contour画等高线图
Mr-Cat伍可猫 人气:0函数画图
以 z = x 2 + y 2 为例
#导入模块 import numpy as np import matplotlib.pyplot as plt #建立步长为0.01,即每隔0.01取一个点 step = 0.01 x = np.arange(-10,10,step) y = np.arange(-10,10,step) #也可以用x = np.linspace(-10,10,100)表示从-10到10,分100份 #将原始数据变成网格数据形式 X,Y = np.meshgrid(x,y) #写入函数,z是大写 Z = X**2+Y**2 #设置打开画布大小,长10,宽6 #plt.figure(figsize=(10,6)) #填充颜色,f即filled plt.contourf(X,Y,Z) #画等高线 plt.contour(X,Y,Z) plt.show()
结果如下
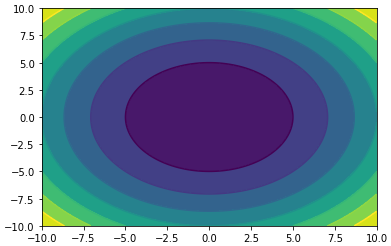
颜色越深表示值越小,中间的黑色表示z=0.
当然,也可以不要颜色填充,并只希望输出z=20和z=40两条线,则在上面代码的基础上,将plt.contourf去掉,并:
#只画z=20和40的线,并将颜色设置为黑色
contour = plt.contour(X,Y,Z,[20,40],colors='k')
#等高线上标明z(即高度)的值,字体大小是10,颜色分别是黑色和红色
plt.clabel(contour,fontsize=10,colors=('k','r'))
结果如下:
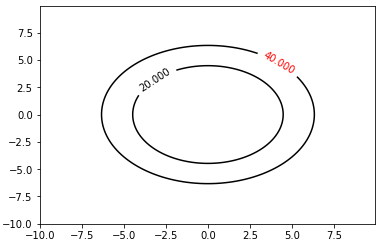
默认是保留3个小数,可以如下保留四位
plt.clabel(contour,fontsize=10,colors=('k','r'),fmt='%.4f')
以下,我将一些常用的功能补充全代码,如下:
#导入模块 import numpy as np import matplotlib.pyplot as plt #建立步长为0.01,即每隔0.01取一个点 step = 0.01 x = np.arange(-10,10,step) y = np.arange(-10,10,step) #也可以用x = np.linspace(-10,10,100)表示从-10到10,分100份 #将原始数据变成网格数据形式 X,Y = np.meshgrid(x,y) #写入函数,z是大写,这里我让中间的0是最大,加了一个负号 Z = -(X**2+Y**2) #填充颜色,f即filled,6表示将三色分成三层,cmap那儿是放置颜色格式,hot表示热温图(红黄渐变) #更多颜色图参考:https://blog.csdn.net/mr_cat123/article/details/80709099 #颜色集,6层颜色,默认的情况不用写颜色层数, cset = plt.contourf(X,Y,Z,6,cmap=plt.cm.hot) #or cmap='hot' #画出8条线,并将颜色设置为黑色 contour = plt.contour(X,Y,Z,8,colors='k') #等高线上标明z(即高度)的值,字体大小是10,颜色分别是黑色和红色 plt.clabel(contour,fontsize=10,colors='k') #去掉坐标轴刻度 #plt.xticks(()) #plt.yticks(()) #设置颜色条,(显示在图片右边) plt.colorbar(cset) #显示 plt.show()

颜色取反
上面展示的是值越大越白,如果想要让红色在内,则只要在颜色名称后加_r即可。其他颜色映射也是如此
cmap='hor_r'
数据画图
如果是已经有第三维(即高)的数据,那么可以通过数据来画图
这里先对mesh.grid作一个解释:
mesh.grid可以将x,y轴变成数组(array),比如
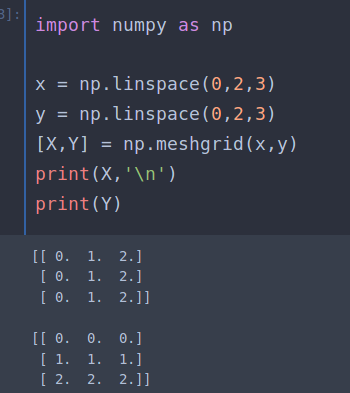
可以看到建立了一个二维平面,详细见:meshgrid应用
比如有:
z = x**2 + y
而z是已经获得的数据,那么如何通过数据将z看成高呢?
import numpy as np
import matplotlib.pyplot as plt
z_list = []
for y in range(3):
for x in range(3):
z = x**2+y
z_list.append(z) #获得z的数据
z = z_list
x = np.linspace(0,2,3)
y = np.linspace(0,2,3)
[X,Y] = np.meshgrid(x,y) #生成X,Y画布,X,Y都是3*3
#因为z是一维,所以要变成3*3
z = np.mat(z)
z = np.array(z)
z.shape = (3,3)
#画图(建议一定要查看X,Y,z是不是一一对应了)
plt.figure(figsize=(10,6))
plt.contourf(x,y,z)
plt.contour(x,y,z)

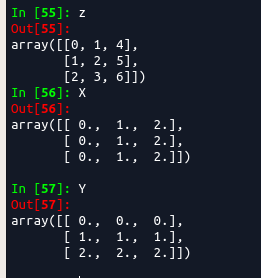
这里输出X,Y和z如下,已经一一对应。
当x=0,y=0,则z=0
当x=0,y=1,则z=1
当x=0,y=2,则z=2
…
…
注意:我上面是用的先for y in xxx,再for x in xxx。
另外,也可以输出x,和y统一操作而不需要再写,也不需要用meshgrid函数
x = np.linspace(xxx)
如下:
import numpy as np
import matplotlib.pyplot as plt
z_list = []
x_list = []
y_list = []
for x in range(3):
for y in range(3):
z = x**2+y
z_list.append(z)
x_list.append(x)
y_list.append(y)
x,y,z = x_list,y_list,z_list
#对x操作
x = np.array(x) #将list变成array
x.shape = (3,3) #重新分成3*3的array
x = np.mat(x).T #变成矩阵并转置,因为array没有转置
#对y操作
y = np.array(y)
y.shape = (3,3)
y = np.mat(y).T
#对z操作
z = np.array(z)
z.shape = (3,3)
z = np.mat(z).T
#画图
plt.figure(figsize=(6,4))
plt.contourf(x,y,z)
plt.contour(x,y,z)


选择性画图
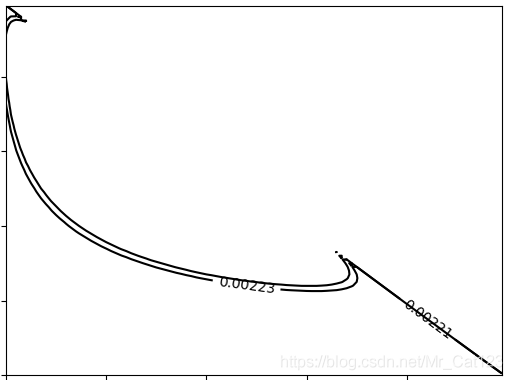
如果我只想画出等高线某些部分的线,比如想画高为0.00221,和0.00223的线,那么可以使用下面命令
contour = plt.contour(X,Y,Z,[0.00221,0.00223],colors='k')
———————————————————我是会卖萌的分割线————————————————————
以下是我的笔记,大家可以选择不看。
例一
已知x+y+z=163,f=f(x,y,z)找出x,y,z对于的值使得f最大
分析:由x+y+z=163可知是有一条线分开,即z=163-x-y,带入f中消掉z,然后再用一个个赋值x,y循环得到f的值,最后采用max挑出f最大的值
由于这里是有四个变量,x,y,z,和f,而x+y+z=163,需要做的是画出横坐标为x,纵坐标为y,高为f的等高线图,跟上面的例子已经不同,上面的例子只有三个变量,x,y,和z,画出x为横坐标,y为纵坐标,z为高的图,所以两者是不同的。不同导致的区别如:
上面的例子得到的x是:
[0, 0, 0, 1, 1, 1, 2, 2, 2]
而下面将讲的得到的x类似是
[0,0,0,1,1,2]
所以需要将缺省的一个1和两个2的位置补上0,同理y和f也是
这里为了快速和简单,只要补充f(下面用z代替了)即可,而x,y可以重新用range生成
注意:这里的z跟代码中的z不同,代码中的z是f的值
#导入模块
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate
from matplotlib import colors
an = []
i = 0
tot = 163
z = np.loadtxt(r'/home/wudl/myfiles/LSPE/data/f90_140_220/FoM1.txt')#加载数据(只加载z坐标这一列)
#生成横纵坐标,并且将横纵坐标对应的点z的值放到空列表an中
for x in range(1,162,1):
for y in range(1,162,1):
if x+y >= 163:
an.append(0)
else:
an.append(z[i])
i += 1
x = np.arange(1,tot-1,1)
y = np.arange(1,tot-1,1)
X,Y = np.meshgrid(x,y)
Z = np.mat(an)
Z.shape = (tot-2,tot-2)
Z = Z.T
#自定义颜色条
colorslist = ['w','gray','aqua']
#将颜色条命名为mylist,一共插值颜色条3000个
cmaps = colors.LinearSegmentedColormap.from_list('mylist',colorslist,N=3000)
#画40层颜色
cset = plt.contourf(X,Y,Z,40,cmap = cmaps)
#画200条线,设置字体大小为10
contour = plt.contour(X,Y,Z,200,colors='k')
plt.clabel(contour,fontsize=10,colors='k')
#坐标轴的字体采用LATEX
plt.xlabel('$n_{90}$',fontsize=20)
plt.ylabel('$n_{220}$',fontsize=20)
#显示颜色条
plt.colorbar(cset)
#显示图片
plt.show()
例二
from __future__ import division
import os
os.chdir('/media/sf_Share/fisher_matrix/myLSPE/LSPE4') #ATTENTION:change work dir
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
import settings
from matplotlib import colors
st = settings.Settings()
data = np.loadtxt(r'/media/sf_Share/fisher_matrix/myLSPE/data/fsky0.7/41+95+150/r_0.01/sigma_F_0.1/sigma_F=0.1/threefre.txt')
#data = np.loadtxt(r'/media/sf_Share/fisher_matrix/myLSPE/data/threefre.txt')
z = data[:,3] #sigma_r
zmin = min(z)
print(zmin)
an = []
i = 0
for x in range(1,st.tot_det-1,st.step): #x_min=1,x_max=161
for y in range(1,st.tot_det-1,st.step):
if x+y >= st.tot_det:
an.append(0)
else:
an.append(z[i])
i += 1
x = np.arange(1,st.tot_det-1,st.step)
y = np.arange(1,st.tot_det-1,st.step)
X,Y = np.meshgrid(x,y)
Z = np.mat(an)
Z.shape = (X.shape[0],X.shape[0])
Z = Z.T
colorslist = ['w','gainsboro','gray','aqua']
#将颜色条命名为mylist,一共插值颜色条50个
cmaps = colors.LinearSegmentedColormap.from_list('mylist',colorslist,N=200)
#cmaps = mpl.cm.hot
#自定义颜色范围,
norm = colors.Normalize(vmin=0.0017,vmax=0.0040)
#cset = plt.contourf(X,Y,Z,100,cmap = 'BuGn')
cset = plt.contourf(X,Y,Z,100,alpha=1,vmin=0.0017,vmax=0.0040,cmap = 'hot_r')
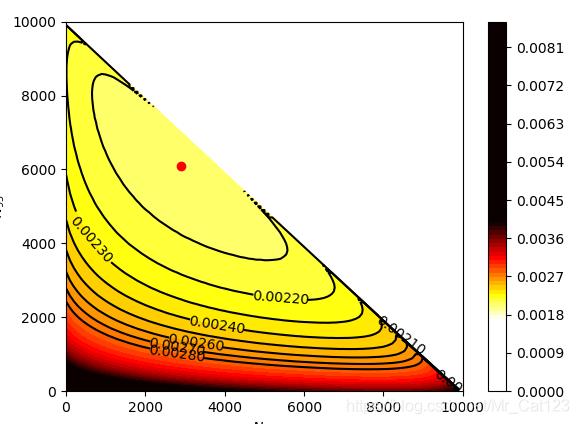
contour = plt.contour(X,Y,Z,[0.00210,0.00220,0.00230,0.00240,0.00250,0.00260,0.00270,0.00280],colors='k')
plt.clabel(contour,fontsize=10,colors='k',fmt='%.5f')
plt.scatter(2901,6101,color='r')
plt.axis([0,10000,0,10000])
plt.colorbar(cset)
#plt.xlabel(str(st.nu[0])+ ' frequency')
#plt.ylabel(str(st.nu[1])+' frequency')
plt.xlabel('$N_{41}$')
plt.ylabel('$N_{95}$')
plt.show()
总结
加载全部内容