Python牛顿迭代算法
Mr.Winter` 人气:01.引例
给定如图所示的某个函数,如何计算函数零点x0
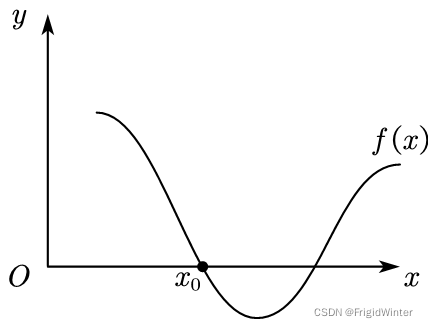
在数学上我们如何处理这个问题?
最简单的办法是解方程f(x)=0,在代数学上还有著名的零点判定定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)⋅f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即至少存在一个c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
然而,数学上的方法并不一定适合工程应用,当函数形式复杂,例如出现超越函数形式;非解析形式,例如递推关系时,精确的方程解析一般难以进行,因为代数上还没发展出任意形式的求根公式。而零点判定定理求解效率也较低,需要不停试错。
因此,引入今天的主题——牛顿迭代法,服务于工程数值计算。
2.牛顿迭代算法求根
记第k轮迭代后,自变量更新为xk,令目标函数f(x)在x=xk泰勒展开:
f(x)=f(xk)+f′(xk)(x−xk)+o(x)
我们希望下一次迭代到根点,忽略泰勒余项,令f(xk+1)=0,则
xk+1=xk−f(xk)/f'(xk)
不断重复运算即可逼近根点。
在几何上,上面过程实际上是在做f(x)在x=xk处的切线,并求切线的零点,在工程上称为局部线性化。如图所示,若xk在x0的左侧,那么下一次迭代方向向右。
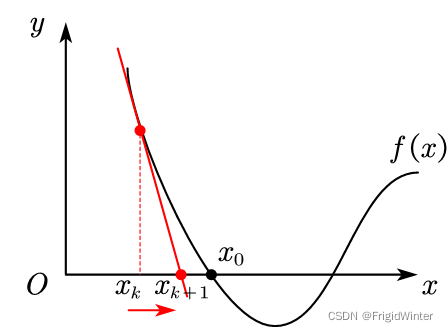
若xk在x0的右侧,那么下一次迭代方向向左。
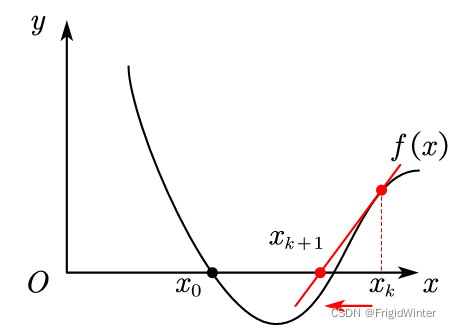
3.牛顿迭代优化
将优化问题转化为求目标函数一阶导数零点的问题,即可运用上面说的牛顿迭代法。
具体地,记第k轮迭代后,自变量更新为xk ,令目标函数f(x)在x=xk泰勒展开:
f(x)=f(xk)+f′(xk)(x−xk)+1/2f′′(xk)(x−xk)2+o(x)
两边求导得
f′(x)=f′(xk)+f′′(xk)(x−xk)
令f′(xk+1)=f′(xk)+f′′(xk)(xk+1−xk)=0,从而得到
xk+1=xk−f′(xk)/f'′(xk)
对于向量x=[x1 x2⋯xd]T,将上述迭代公式推广为
xk+1=xk−[∇2f(xk)]−1∇f(xk)
其中∇2f(xk)是Hessian矩阵,当其正定时可以保证牛顿优化算法往 减小的方向迭代
牛顿法的特点如下:
① 以二阶速率向最优点收敛,迭代次数远小于梯度下降法,优化速度快;
梯度下降法的解析参考图文详解梯度下降算法的原理及Python实现
②学习率为[∇2f(xk)]−1 ,包含更多函数本身的信息,迭代步长可实现自动调整,可视为自适应梯度下降算法;
③ 耗费CPU计算资源多,每次迭代需要计算一次Hessian矩阵,且无法保证Hessian矩阵可逆且正定,因而无法保证一定向最优点收敛。
在实际应用中,牛顿迭代法一般不能直接使用,会引入改进来规避其缺陷,称为拟牛顿算法簇,其中包含大量不同的算法变种,例如共轭梯度法、DFP算法等等,今后都会介绍到。
4 代码实战:Logistic回归
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import matplotlib as mpl
from Logit import Logit
'''
* @breif: 从CSV中加载指定数据
* @param[in]: file -> 文件名
* @param[in]: colName -> 要加载的列名
* @param[in]: mode -> 加载模式, set: 列名与该列数据组成的字典, df: df类型
* @retval: mode模式下的返回值
'''
def loadCsvData(file, colName, mode='df'):
assert mode in ('set', 'df')
df = pd.read_csv(file, encoding='utf-8-sig', usecols=colName)
if mode == 'df':
return df
if mode == 'set':
res = {}
for col in colName:
res[col] = df[col].values
return res
if __name__ == '__main__':
# ============================
# 读取CSV数据
# ============================
csvPath = os.path.abspath(os.path.join(__file__, "../../data/dataset3.0alpha.csv"))
dataX = loadCsvData(csvPath, ["含糖率", "密度"], 'df')
dataY = loadCsvData(csvPath, ["好瓜"], 'df')
label = np.array([
1 if i == "是" else 0
for i in list(map(lambda s: s.strip(), list(dataY['好瓜'])))
])
# ============================
# 绘制样本点
# ============================
line_x = np.array([np.min(dataX['密度']), np.max(dataX['密度'])])
mpl.rcParams['font.sans-serif'] = [u'SimHei']
plt.title('对数几率回归模拟\nLogistic Regression Simulation')
plt.xlabel('density')
plt.ylabel('sugarRate')
plt.scatter(dataX['密度'][label==0],
dataX['含糖率'][label==0],
marker='^',
color='k',
s=100,
label='坏瓜')
plt.scatter(dataX['密度'][label==1],
dataX['含糖率'][label==1],
marker='^',
color='r',
s=100,
label='好瓜')
# ============================
# 实例化对数几率回归模型
# ============================
logit = Logit(dataX, label)
# 采用牛顿迭代法
logit.logitRegression(logit.newtomMethod)
line_y = -logit.w[0, 0] / logit.w[1, 0] * line_x - logit.w[2, 0] / logit.w[1, 0]
plt.plot(line_x, line_y, 'g-', label="牛顿迭代法")
# 绘图
plt.legend(loc='upper left')
plt.show()
其中更新权重代码为
'''
* @breif: 牛顿迭代法更新权重
* @param[in]: None
* @retval: 优化参数的增量dw
'''
def newtomMethod(self):
wTx = np.dot(self.w.T, self.X).reshape(-1, 1)
p = Logit.sigmod(wTx)
dw_1 = -self.X.dot(self.y - p)
dw_2 = self.X.dot(np.diag((p * (1 - p)).reshape(self.N))).dot(self.X.T)
dw = np.linalg.inv(dw_2).dot(dw_1)
return dw
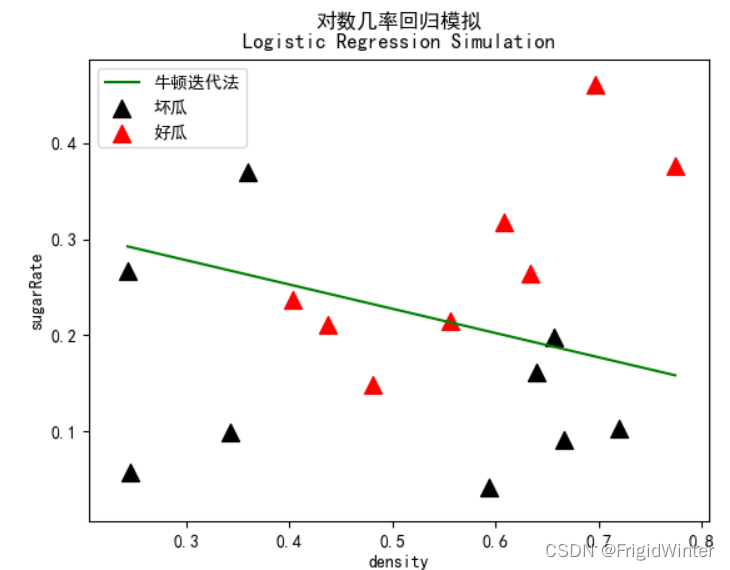
加载全部内容