Python Scipy概率分布
nejssd 人气:0Scipy自带了多种常见的分布,如正态分布、均匀分布、二项分布、多项分布、伽马分布等等,还可以自定义任意的概率分布。本文将介绍如何利用Scipy自定义任意的概率分布。
连续变量分布
考虑连续变量x满足如下概率密度分布函数:
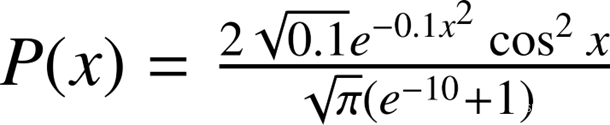
其在实数域积分为1。我们可以通过scipy.stats中的rv_continuous类去实现这个分布,代码如下:
from scipy.stats import rv_continuous
import matplotlib.pyplot as plt
import numpy as np
class MyDistribution(rv_continuous):
def _pdf(self, x):#概率密度分布函数
return 2*sqrt(0.1)*exp(-0.1*x**2)*cos(x)**2/(sqrt(pi)*(exp(-10) + 1))
distribution = MyDistribution()
xlist=np.linspace(-8,8,300)
ylist=distribution.pdf(xlist)
samples=distribution.rvs(size=200);#取200次样
fig,ax=plt.subplots(figsize=(8,6))
ax.plot(xlist,ylist,lw=3,color='red',label="$\mathrm{ideal}$");
ax.hist(samples,color='blue',density=True, bins=np.arange(-8,8,0.25), histtype='barstacked', rwidth=0.9,label=r"$\mathrm{samples}$")
ax.legend(fontsize=20);
ax.set_xlabel(r"$x$",size=25)
ax.set_ylabel(r"$\mathrm{PDF}$",size=20)
ax.set_xlim(-8,8);
ax.tick_params(axis='both',direction='in',width=1.3,length=3,top=1,right=1,labelsize=20,pad=2)
fig.tight_layout();
fig.show();
运行结果如下:
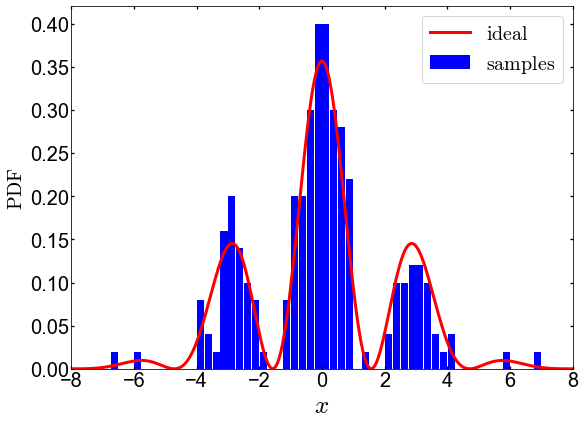
增加采样次数,分布直方图逐渐趋于理想的概率分布函数P(x)。
离散变量分布
考虑连续变量x满足泊松分布,则可以用scipy.stats中的rv_discrete类去实现这个分布,代码如下:
from scipy.stats import rv_discrete
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import factorial
class MyDistribution(rv_discrete):
def _pmf(self, k, mu):
return exp(-mu)*mu**k/factorial(k)
distribution = MyDistribution()
mu=2
samples=distribution.rvs(size=500,mu=mu);#取500次样
klist = np.arange(0,10,1)
plist = distribution.pmf(klist,mu)
fig, ax = plt.subplots()
ax.plot(klist, plist, 'ro', ms=12, mec='r',label="$\mathrm{ideal}$");
ax.hist(samples,color='blue',density=True, bins=klist, histtype='barstacked', rwidth=0.8,label=r"$\mathrm{samples}$",align="left")
ax.legend(fontsize=20);
fig.show();
运行结果如下:

可以修改上述MyDistribution类中的pmf函数,实现任意想要的离散分布。
二项分布Binomial Distribution
是n个独立的成功/失败试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当n=1时,二项分布就是伯努利分布。
'''1、定义随机变量''' # 比如5次掷硬币实验,正面朝上的次数 n2=5 x2=np.arange(1,n2+1,1) x2
array([1, 2, 3, 4, 5])
'''2、求对应的概率质量函数 (PMF)''' p2=0.5 pList2=stats.binom.pmf(x2,n2,p2) # 返回一个列表,列表中每个元素表示随机变量中对应值的概率 pList2
array([0.15625, 0.3125 , 0.3125 , 0.15625, 0.03125])
'''3、绘图'''
fig=plt.figure()
# plot在此的作用为显示两个标记点
plt.plot(x2,pList2,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值)
'''
plt.vlines(x2, 0, pList2)
plt.xlabel('随机变量:抛硬币5次')
plt.ylabel('概率')
plt.title('二项分布:n=%d,p2=%0.2f' % (n2,p2))
plt.show()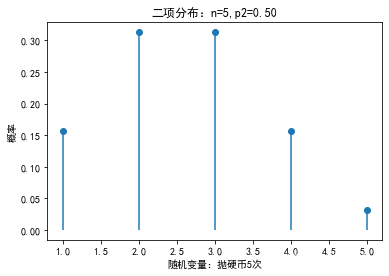
几何分布Geometric Distribution
在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
'''1、定义随机变量''' # 比如射箭1次中靶的概率为90%,射5次箭 k=5 x3=np.arange(1,k+1,1) x3
array([1, 2, 3, 4, 5])
'''2、求对应的概率质量函数 (PMF)''' p3=0.7 pList3=stats.geom.pmf(x3,p3) # 返回一个列表,表示在第i次射击中,第一次射中的概率 pList3
array([0.7 , 0.21 , 0.063 , 0.0189 , 0.00567])
'''3、绘图'''
fig=plt.figure()
# plot在此的作用为显示两个标记点
plt.plot(x3,pList3,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值)
'''
plt.vlines(x3, 0, pList3)
plt.xlabel('随机变量:射击5次')
plt.ylabel('概率')
plt.title('几何分布:n=%d,p=%0.2f' % (k,p3))
plt.show()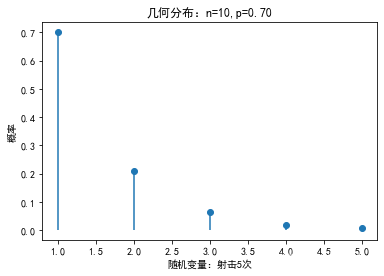
泊松分布Poisson Distribution
描述在某单位时间内,事件发生n次的概率
'''1、定义随机变量''' # 某机器每季度发生故障平均为1次,那么在一年中机器发生10次的概率为 mu=4 # 平均值 k=10 # 要求发生10次的概率 x4=np.arange(1,k+1,1) x4
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
'''2、求对应的概率质量函数 (PMF)''' pList4=stats.poisson.pmf(x4,mu) # 一年的平均值为4 # 返回一个列表,表示1年中发生i次故障的概率 pList4
array([0.07326256, 0.14652511, 0.19536681, 0.19536681, 0.15629345,
0.10419563, 0.05954036, 0.02977018, 0.01323119, 0.00529248])
'''3、绘图'''
fig=plt.figure()
# plot在此的作用为显示两个标记点
plt.plot(x4,pList4,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值)
'''
plt.vlines(x4, 0, pList4)
plt.xlabel('随机变量:发生k次故障')
plt.ylabel('概率')
plt.title('泊松分布:n=%d' % k)
plt.show()
加载全部内容