C语言 数学与DP问题
小羊努力变强 人气:0数学
顾名思义,数学类的题就是都可以用数学知识求解。
买不到的数目
这是第四届蓝桥杯省赛C++A组,第四届蓝桥杯省赛JAVAC组的一道题
小明开了一家糖果店。
他别出心裁:把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。
大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式
两个正整数 n,m,表示每种包装中糖的颗数。
输出格式
一个正整数,表示最大不能买到的糖数。
数据范围
2≤n,m≤1000,
保证数据一定有解。
输入样例:
4 7
输出样例:
17
这道题简单看一下,似乎没有什么规律,我们可以先打表来找一下规律:
#include <bits/stdc++.h>
using namespace std;
//给定一个m,是否能用p和q凑出来
bool dfs(int m,int p,int q)
{
if(m == 0) return true;
if(m >= p && dfs(m - p,p,q)) return true;
if(m >= q && dfs(m - q,p,q)) return true;
return false;
}
int main()
{
int p,q;
cin >> p >> q;
int res = 0;
for(int i = 1; i <= 1000;i ++)
{
if(!dfs(i,p,q)) res = i;
}
cout << res << endl;
return 0;
}
打表暴力搜索找规律
2 3 输出 1
3 5 输出7
3 7 输出11
3 10 输出17
...
最后得到规律
如果 a,b均是正整数且互质,那么由 ax+by,x≥0,y≥0ax+by,x≥0,y≥0 不能凑出的最大数是 (a−1)(b−1)−1。
接下来再看数学代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int p, q;
cin >> p >> q;
cout << (p - 1) * (q - 1) - 1 << endl;
return 0;
}
蚂蚁感冒
这也是蓝桥杯的一道题,来源:第五届蓝桥杯省赛C++A/B组
长 100 厘米的细长直杆子上有 n 只蚂蚁。
它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是 1 厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有 1 只蚂蚁感冒了。
并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
输入格式
第一行输入一个整数 n, 表示蚂蚁的总数。
接着的一行是 n 个用空格分开的整数 Xi, Xi 的绝对值表示蚂蚁离开杆子左边端点的距离。
正值表示头朝右,负值表示头朝左,数据中不会出现 0 值,也不会出现两只蚂蚁占用同一位置。
其中,第一个数据代表的蚂蚁感冒了。
输出格式
输出1个整数,表示最后感冒蚂蚁的数目。
数据范围
1<n<50,
0<|Xi|<100
输入样例1:
3
5 -2 8
输出样例1:
1
输入样例2:
5
-10 8 -20 12 25
输出样例2:
3
这题很有意思,只读题就会有这种想法,如果一只蚂蚁从左往右走,另外一只从右往左走,有一只感冒了,那么,他们相遇后就会分别向相反的方向走。
按照这个思路,我们来写一个暴力解法:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, pos;
int a[N];
int ans = 1;
int cmp(int a, int b)
{
return abs(a) < abs(b);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
int pre = a[0];
sort(a, a + n, cmp); //先按绝对值 将蚂蚁的位置排好
for (int i = 0; i < n; i++)
{
if (a[i] == pre)
pos = i;
}
int flag = 0;
if (pre > 0) //首先感染的蚂蚁向右走
{
for (int i = pos + 1; i < n; i++)
{
if (a[i] > 0)
continue;
if (a[i] < 0)
{
ans++;
flag = 1; //标记右面有蚂蚁向左走
}
}
for (int i = pos - 1; i >= 0; i--)
{
if (flag) //在右边有往左走的蚂蚁前提下
{
if (a[i] > 0) //如果左面有向右走的那么肯定会传染
ans++;
}
}
}
if (pre < 0) //首先感染的蚂蚁向左走,方法同上
{
for (int i = pos - 1; i >= 0; i--)
{
if (a[i] < 0)
continue;
if (a[i] > 0)
{
ans++;
flag = 1;
}
}
for (int i = pos + 1; i < n; i++)
{
if (a[i] > 0)
continue;
if (flag)
{
if (a[i] < 0)
ans++;
}
}
}
cout << ans << endl;
return 0;
}
但这中间就有一个很有意思的地方就是左边的往右走,右边的往左走,有一只感冒了,它们相遇后还是等价于有两只蚂蚁分别往前走,只是这样两只蚂蚁都感冒了,这样之后遇到的蚂蚁也会被感冒,这样想就不会有掉头做判断这一步了,接下来请看代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int n;
int x[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> x[i];
int left = 0, right = 0; // 分别表示左边向右走的蚂蚁数量,和右边向左走的蚂蚁数量
for (int i = 1; i < n; i ++ )
if (abs(x[i]) < abs(x[0]) && x[i] > 0) left ++ ;
else if (abs(x[i]) > abs(x[0]) && x[i] < 0) right ++ ;
if (x[0] > 0 && right == 0 || x[0] < 0 && left == 0) cout << 1 << endl;
else cout << left + right + 1 << endl;
return 0;
}
饮料换购
来源:第六届蓝桥杯省赛C++A/C组,第六届蓝桥杯省赛JAVAB组
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的 n 瓶饮料,最后他一共能喝到多少瓶饮料。
输入格式
输入一个整数 n,表示初始买入的饮料数量。
输出格式
输出一个整数,表示一共能够喝到的饮料数量。
数据范围
0<n<10000
输入样例:
100
输出样例:
149
这题就很简单了,还是先看模拟代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
int res = n;
while (n >= 3)
{
res += n / 3;
n = n / 3 + n % 3;
}
cout << res << endl;
return 0;
}
然后是数学公式代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
cout << n + (n - 1) / 2 << endl;
return 0;
}
简单DP
先来看题:01背包问题是非常经典的DP问题。
01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
题目介绍
有 N 件物品和一个容量为 V的背包,每件物品有各自的价值且只能被选择一次,要求在有限的背包容量下,装入的物品总价值最大。
「0-1 背包」是较为简单的动态规划问题,也是其余背包问题的基础。
动态规划是不断决策求最优解的过程,「0-1 背包」即是不断对第 i个物品的做出决策,「0-1」正好代表不选与选两种决定
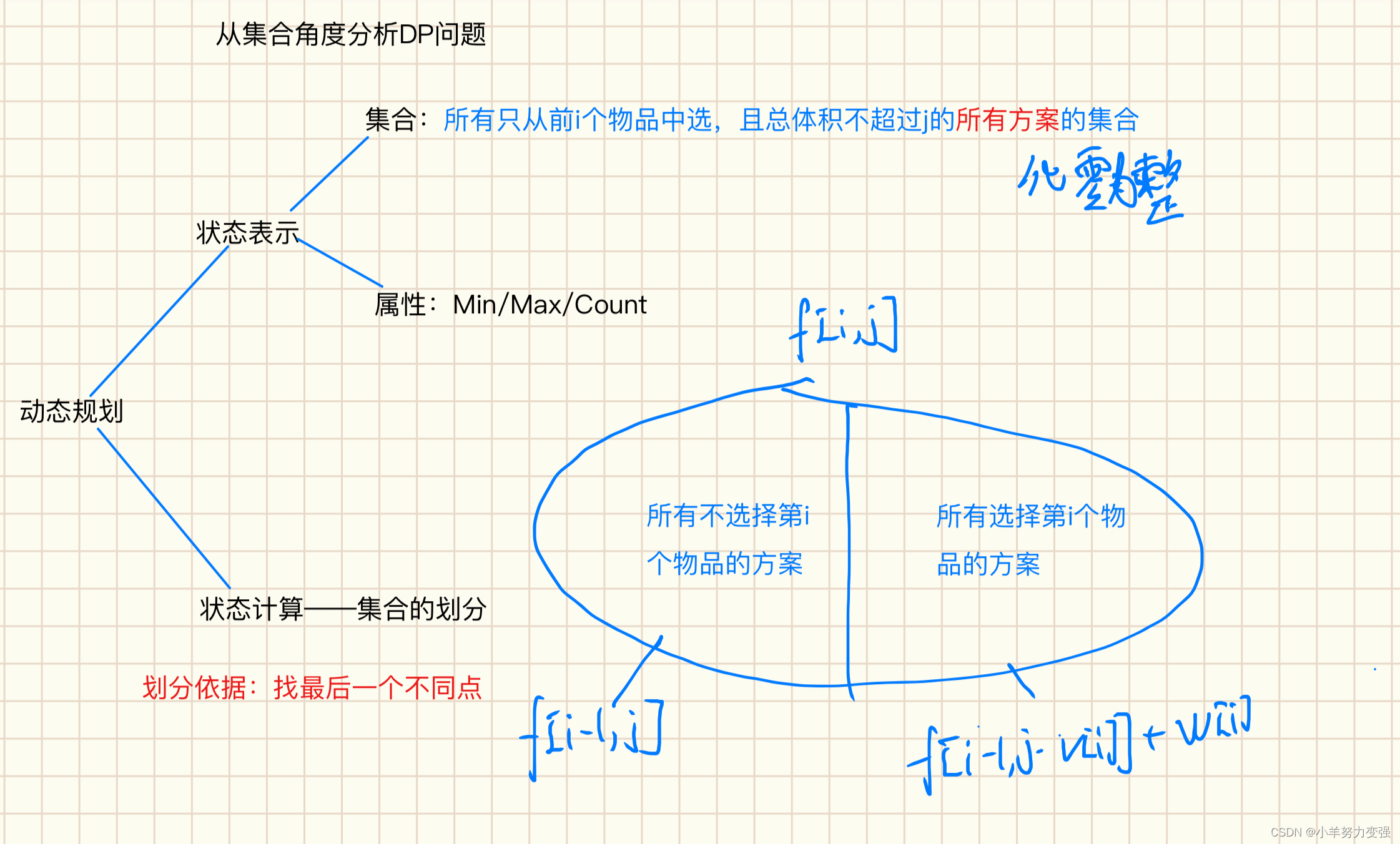
二维
(1)状态f[i][j]定义:前 i个物品,背包容量 j 下的最优解(最大价值):
当前的状态依赖于之前的状态,可以理解为从初始状态f[0][0] = 0开始决策,有 N 件物品,则需要 N 次决策,每一次对第 i 件物品的决策,状态f[i][j]不断由之前的状态更新而来。
(2)当前背包容量不够(j < v[i]),没得选,因此前 i个物品最优解即为前 i−1个物品最优解:
对应代码:f[i][j] = f[i - 1][j]。
(3)当前背包容量够,可以选,因此需要决策选与不选第 i 个物品:
选:f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选:f[i][j] = f[i - 1][j] 。
我们的决策是如何取到最大价值,因此以上两种情况取 max() 。
接下来请看二维求解代码:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int v[MAXN]; // 体积
int w[MAXN]; // 价值
int f[MAXN][MAXN]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
// 当前背包容量装不进第i个物品,则价值等于前i-1个物品
if(j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
一维
将状态f[i][j]优化到一维f[j],实际上只需要做一个等价变形。
原式:f[i][j] = max(f[i-1][j], f[i - 1][j - v[i]] + w[i]);
改成一维:f[j] = max(f[j], f[j - v[i]] + w[i]);
先来看代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N];
int v[N], w[N];
int n, m;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++) {
for (int j = m; j >= v[i]; j--)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
}这中间有一个点大家可能不太好理解,为什么是for (int j = m; j >= v[i]; j--),而不是for (int j = v[i]; j <= m; j++)
首先我们先来模拟一下如果是for (int j = v[i]; j <= m; j++),循环就是:
for (int i = 1; i <= n; i++) {
for (int j = v[i]; j <= m; j++) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
来看题
输入样例
4 5
1 2
2 4
3 4
4 5
物品 体积 价值
i=1 1 2
i=2 2 4
i=3 3 4
i=4 4 5
当还没进循环的时候
f[0] = 0; f[1] = 0; f[2] = 0; f[3] = 0; f[4] = 0; f[5] = 0;
当进入循环 i == 1 时:v[i]=1,w[i]=2;
j=1:f[1]=max(f[1],f[1-1]+2),即max(0,2)=2;即f[1]=2;
j=2:f[2]=max(f[2],f[2-1]+2),即max(0,4)=4;即f[2]=4;
j=3:f[3]=max(f[3],f[3-1]+2),即max(0,6)=6;即f[3]=6;
j=4:f[4]=max(f[4],f[4-1]+2),即max(0,8)=8;即f[4]=8;
j=5:f[5]=max(f[5],f[5-1]+2),即max(0,10)=10;即f[5]=10;
当到这里的时候就已经出问题了。
//如果 j 层循环是逆序的: for (int i = 1; i <= n; i++) {<!--{C}%3C!%2D%2D%20%2D%2D%3E--> for (int j = m; j >= v[i]; j--) {<!--{C}%3C!%2D%2D%20%2D%2D%3E--> f[j] = max(f[j], f[j - v[i]] + w[i]); } }//如果 j 层循环是逆序的:
for (int i = 1; i <= n; i++) {
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
输入样例
4 5
1 2
2 4
3 4
4 5
物品 体积 价值
i=1 1 2
i=2 2 4
i=3 3 4
i=4 4 5
当还没进循环的时候
f[0] = 0; f[1] = 0; f[2] = 0; f[3] = 0; f[4] = 0; f[5] = 0;
当进入循环时i==1,w[i]=2,v[i]=1;
j=5:f[5]=max(f[5],f[5-1]+2),即max(0,2)=2;即f[5]=2;
j=4:f[4]=max(f[4],f[4-1]+2),即max(0,2)=2;即f[4]=2;
j=3:f[3]=max(f[3],f[3-1]+2),即max(0,2)=2;即f[3]=2;
j=2:f[2]=max(f[2],f[2-1]+2),即max(0,2)=2;即f[2]=2;
j=1:f[1]=max(f[1],f[1-1]+2),即max(0,2)=2;即f[1]=2;
当进入循环 i == 2 时,w[i]=4,v[i]=2;
j=5:f[5]=max(f[5],f[5-2]+4),即max(2,6)=6,即f[5]=6;
j=4:f[5]=max(f[4],f[4-2]+4),即max(2,6)=6,即f[4]=6;
j=3:f[5]=max(f[3],f[3-2]+4),即max(2,6)=6,即f[3]=6;
j=2:f[5]=max(f[2],f[2-2]+4),即max(2,4)=4,即f[2]=4;
当进入循环 i == 3 时: w[i] = 4; v[i] = 3;
j=5:f[5]=max(f[5],f[5-3]+4),即max(6,8)=8,即f[5]=8;
j=4:f[4]=max(f[4],f[4-3]+4),即max(6,6)=6,即f[4]=6;
j=3:f[3]=max(f[3],f[3-3]+4),即max(6,4)=6,即f[3]=6;
当进入循环 i == 3 时: w[i] = 5; v[i] = 4;
j=5:f[5]=max(f[5],f[5-4]+5),即max(8,7)=8,即f[5]=8;
j=4:f[4]=max(f[4],f[4-4]+5),即max(6,5)=6,即f[4]=6;
模拟结束,最后max=8:发现没有错误,即逆序就可以解决这个优化的问题了
最后为什么一维情况下枚举背包容量需要逆序?
在二维情况下,状态f[i][j]是由上一轮i - 1的状态得来的,f[i][j]与f[i - 1][j]是独立的。而优化到一维后,如果我们还是正序,则有f[较小体积]更新到f[较大体积],则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
简单来说,一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」,逆序则不会有这样的问题。
加载全部内容