C语言 线性DP
小羊努力变强 人气:0写在前面
之前讲过背包问题,不知道大家忘了吗,如果忘了可以点这里,这次是线性DP
数字三角形
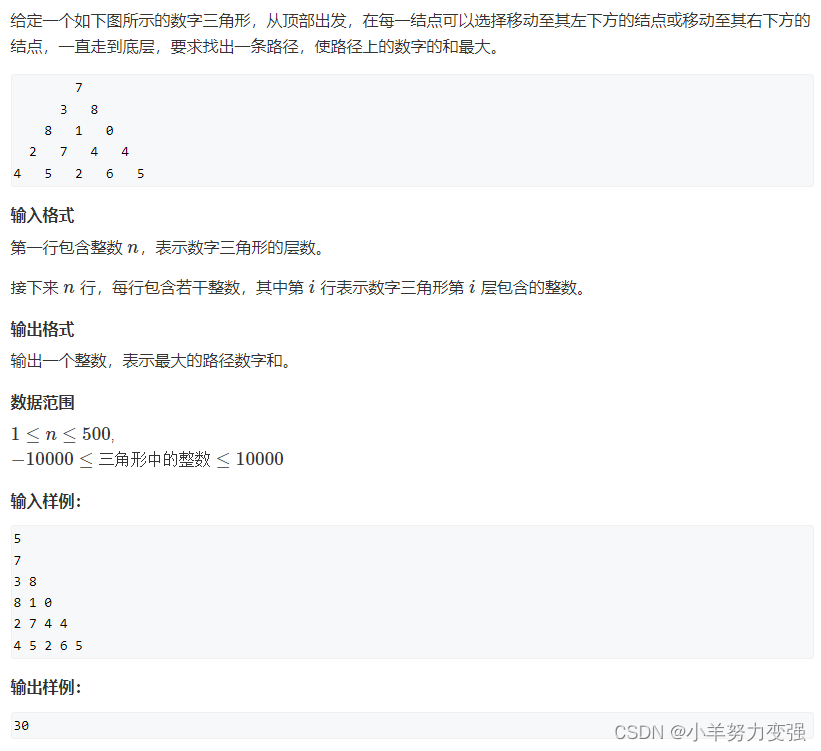
状态表示:f[i,j],到点i,j的最大路径
状态计算:f[i,j] = MAX(f[i-1,j-1]+a[i,j],f[i-1,j]+a[i,j])
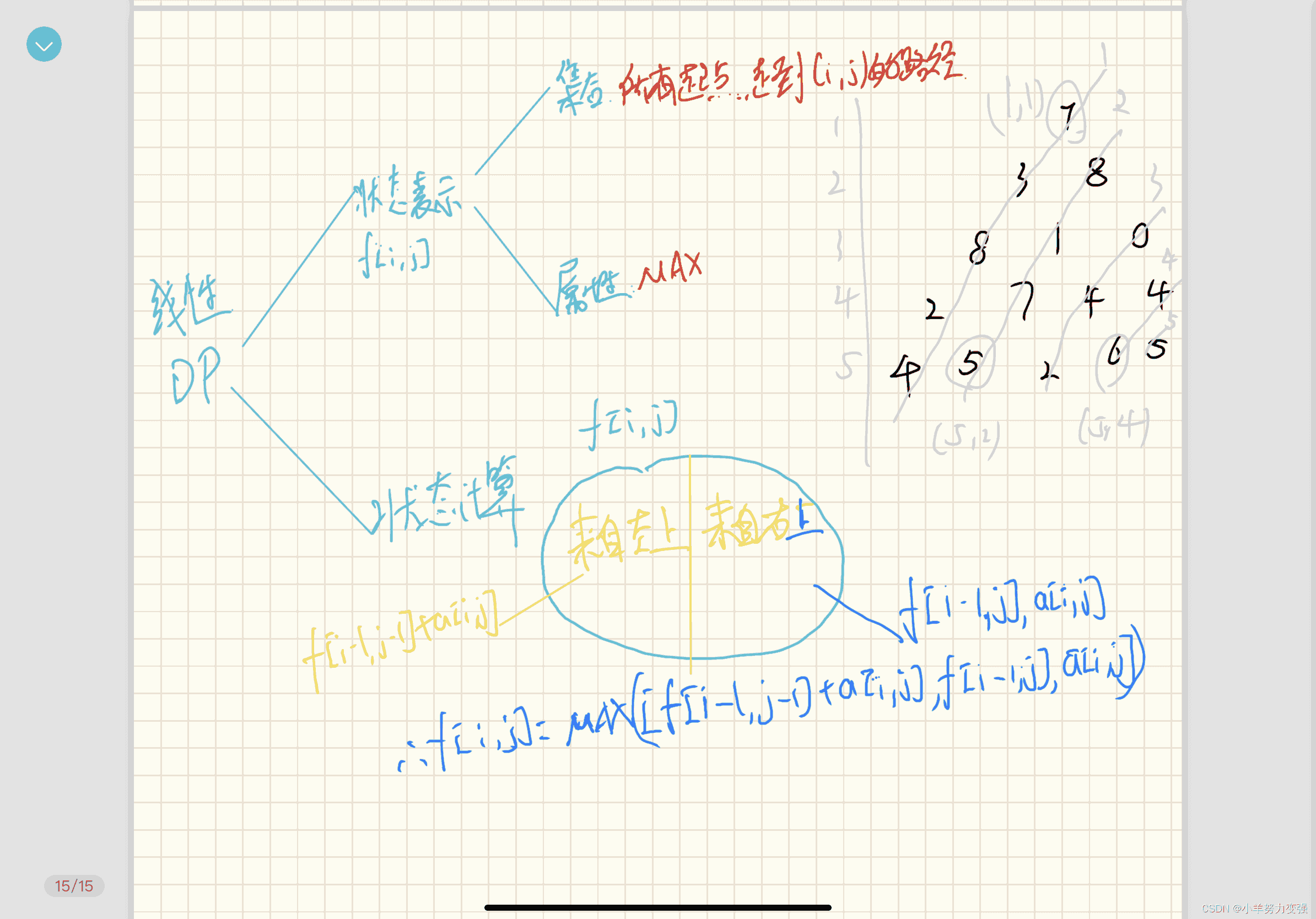
看图,以例题为例,将它看成五行五列的三角形,每个点都可以用坐标表示。那么我们可以得知到一个数的最大路径要么来自左上,要么来自右上。左上的数用f[i-1,j-1]表示,右上的数f[i-1,j]表示,因此我们就有了状态转移公式:
f[i,j] = MAX(f[i-1,j-1]+a[i,j],f[i-1,j]+a[i,j])
所以就有了最终的代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N];
int f[N][N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
scanf("%d", &a[i][j]);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= i + 1; j ++ )//注意这里j从0到i+1,因为对于边界点,它的上一层只有一条路径通向它
f[i][j] = -INF;//初始化近似为-∞
f[1][1] = a[1][1];
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
printf("%d\n", res);
return 0;
}
最长上升子序列
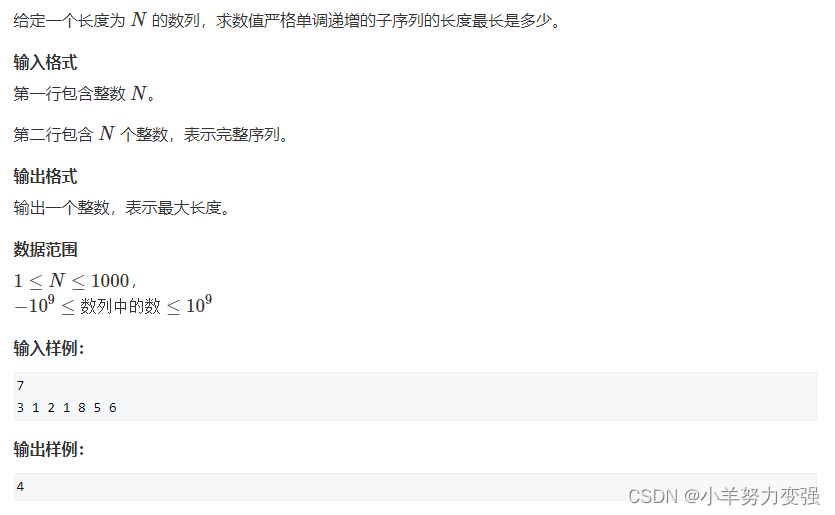
状态表示:f[i]表示从第一个数字开始算,以w[i]结尾的最大的上升序列。(以w[i]结尾的所有上升序列中属性为最大值的那一个)
状态计算(集合划分):j∈(0,1,2,…,i-1), 在w[i] > w[j]时,
f[i] = max(f[i], f[j] + 1)。
有一个边界,若前面没有比i小的,f[i]为1(自己为结尾)。
最后在找f[i]的最大值。
时间复杂度
O(n2) 状态数(n) * 转移数(n)
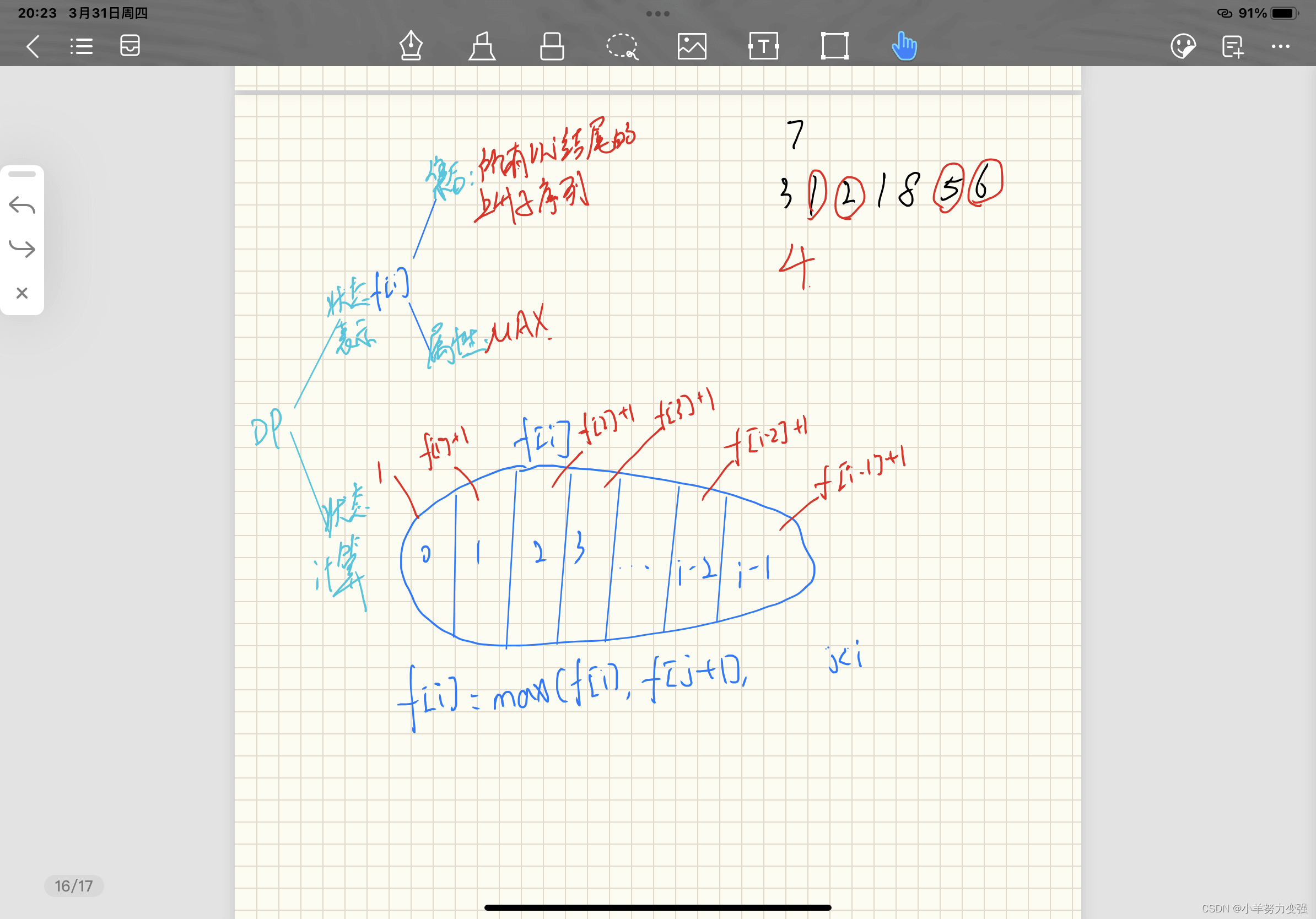
看图, 首先 f[i]f[i] 的含义是以 w[i]结尾的最长上升子序列的长度
初始值 f[i]=1,i∈[0,n−1],表示自己就是最长上升子序列,长度为 1
接下来考虑状态转移,把前 i−1个数字中所有满足条件 w[j]<w[i](因为要求是上升子序列) 的 j 找出来,那么 f[i] 就可以试着更新为以 w[j] 结尾的最长上升子序列的长度 再加上 自己的长度 1,但可能更新完的结果没有之前更新过的 f[i] 大,最后两者取一个 max,所以状态转移方程就是 f[i]=max(f[i],f[j]+1)
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int w[N], f[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> w[i];
int mx = 1; // 找出所计算的f[i]之中的最大值,边算边找
for (int i = 0; i < n; i++) {
f[i] = 1; // 设f[i]默认为1,找不到前面数字小于自己的时候就为1
for (int j = 0; j < i; j++) {
if (w[i] > w[j]) f[i] = max(f[i], f[j] + 1); // 前一个小于自己的数结尾的最大上升子序列加上自己,即+1
}
mx = max(mx, f[i]);
}
cout << mx << endl;
return 0;
}
最长上升子序列 II
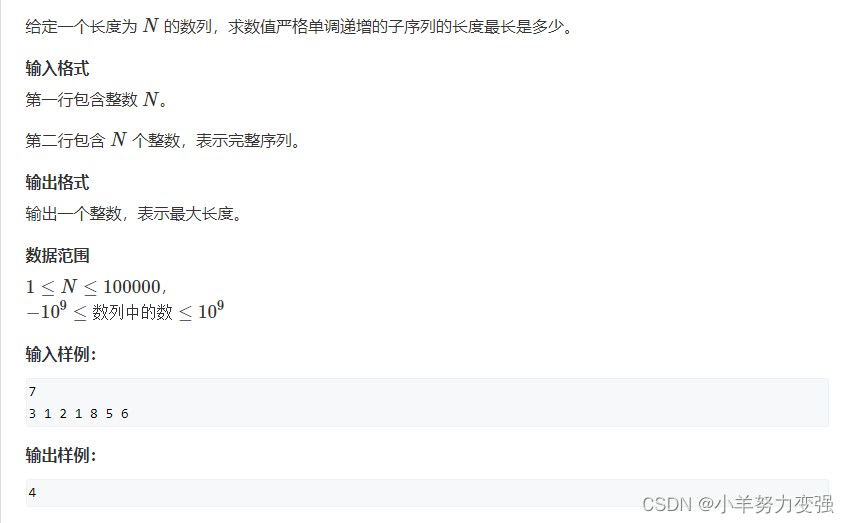
会发现II的数据范围变了,那我们就得做优化,怎么优化呢?
状态表示:f[i]表示长度为i的最长上升子序列,末尾最小的数字。(长度为i的最长上升子序列所有结尾中,结尾最小min的) 即长度为i的子序列末尾最小元素是什么。
状态计算:对于每一个w[i], 如果大于f[cnt-1] (下标从0开始,cnt长度的最长上升子序列,末尾最小的数字),那就cnt+1,使得最长上升序列长度+1,当前末尾最小元素为w[i]。 若w[i]小于等于f[cnt-1],说明不会更新当前的长度,但之前末尾的最小元素要发生变化,找到第一个 大于或等于 (这里不能是大于) w[i],更新以那时候末尾的最小元素。
f[i]一定以一个单调递增的数组,所以可以用二分法来找第一个大于或等于w[i]的数字。
时间复杂度
O(nlogn)状态数(n) * 转移数(logn)
#include <iostream>
using namespace std;
const int N = 1010;
int n, cnt;
int w[N], f[N];
int main() {
cin >> n;
for (int i = 0 ; i < n; i++) cin >> w[i];
f[cnt++] = w[0];
for (int i = 1; i < n; i++) {
if (w[i] > f[cnt-1]) f[cnt++] = w[i];
else {
int l = 0, r = cnt - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (f[mid] >= w[i]) r = mid;
else l = mid + 1;
}
f[r] = w[i];
}
}
cout << cnt << endl;
return 0;
}
最长公共子序列
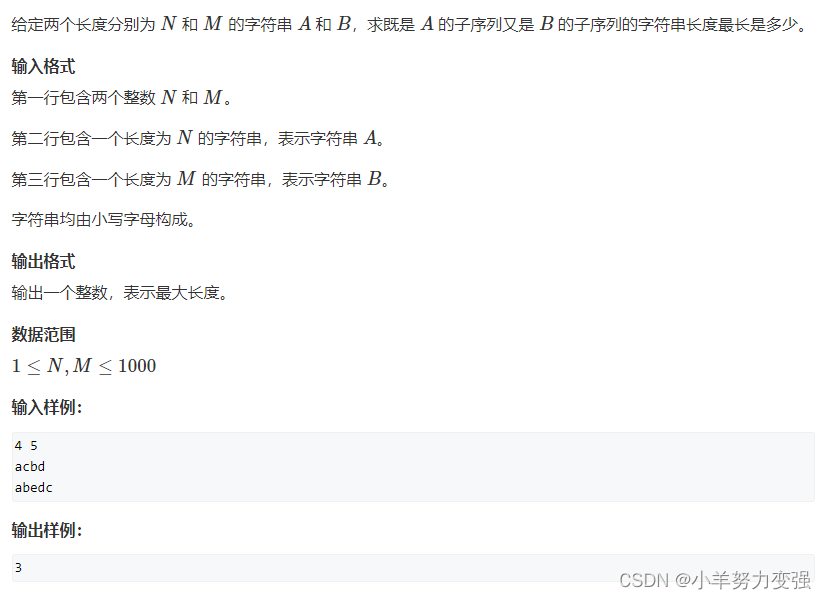
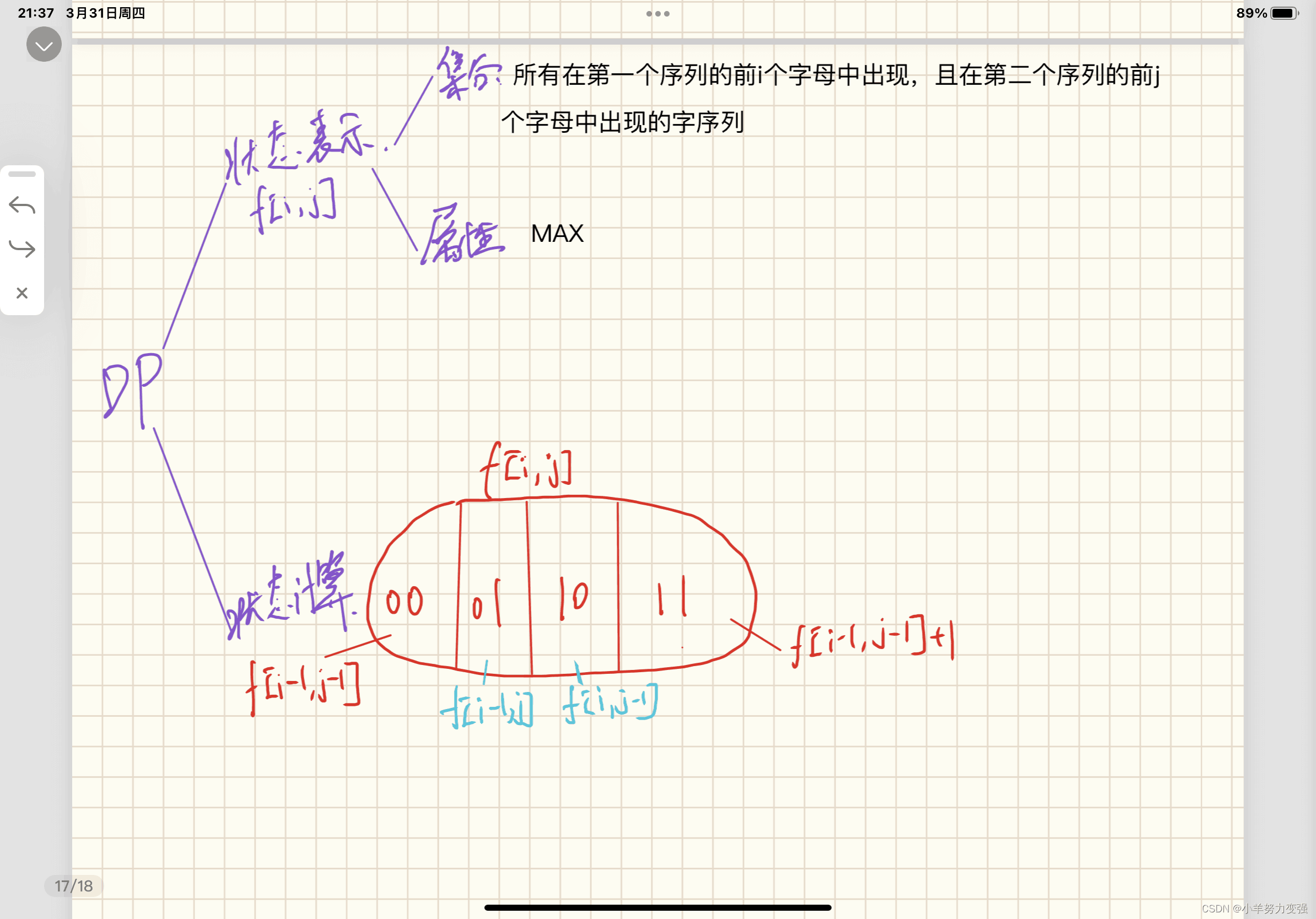
集合表示:f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
集合划分:以a[i],b[j]是否包含在子序列当中为依据,因此可以分成四类:
- ①a[i]不在,b[j]不在
max=f[i−1][j−1]
- ②a[i]a[i]不在,b[j]b[j]在
看似是max=f[i−1][j] , 实际上无法用f[i−1][j]表示,因为f[i−1][j]表示的是在a的前i-1个字母中出现,并且在b的前j个字母中出现,此时b[j]不一定出现,这与条件不完全相等,条件给定是a[i]一定不在子序列中,b[j]一定在子序列当中,但仍可以用f[i−1][j]来表示,原因就在于条件给定的情况被包含在f[i−1][j]中,即条件的情况是f[i−1][j]的子集,而求的是max,所以对结果不影响。
例如:要求a,b,c的最大值可以这样求:max(max(a,b),max(b,c))虽然b被重复使用,但仍能求出max,求max只要保证不漏即可。
- ③a[i],b[j]不在 原理同②
- ④a[i]在,b[j]在 max=f[i−1][j−1]+1
实际上,在计算时,①包含在②和③的情况中,所以①不用考虑
#include <iostream>
using namespace std;
const int N = 1010;
int n , m;
char a[N] , b[N];
int f[N][N];
int main()
{
cin >> n >> m;
cin >> a + 1 >> b + 1;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
{
f[i][j] = max(f[i - 1][j] , f[i][j - 1]);//2和3的情况一定存在,所以可以无条件优先判断
if(a[i] == b[j]) f[i][j] = max(f[i][j] , f[i - 1][j - 1] + 1);
}
cout << f[n][m] << endl;
return 0;
}
加载全部内容