Python实现线性回归
是梦吧,是你吧! 人气:01、概述
(1)人工智能学习

(2)机器学习
(3)有监督学习

(4)线性回归

2、线性回归
(1)实现步骤
- 根据随机初始化的 w x b 和 y 来计算 loss
- 根据当前的 w x b 和 y 的值来计算梯度
- 更新梯度,循环将新的 w′ 和 b′ 复赋给 w 和 b ,最终得到一个最优的 w′ 和 b′ 作为方程最终的
(2)数学表达式

3、代码实现(Python)
(1)机器学习库(sklearn.linear_model)

代码:
from sklearn import linear_model
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt#用于作图
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
import numpy as np#用于创建向量
reg=linear_model.LinearRegression(fit_intercept=True,normalize=False)
x=[[32.50235],[53.4268],[61.53036],[47.47564],[59.81321],[55.14219],[52.14219],[39.29957],
[48.10504],[52.55001],[45.41873],[54.35163],[44.16405],[58.16847],[56.72721]]
y=[31.70701,68.7776,62.56238,71.54663,87.23093,78.21152,79.64197,59.17149,75.33124,71.30088,55.16568,82.47885,62.00892
,75.39287,81.43619]
reg.fit(x,y)
k=reg.coef_#获取斜率w1,w2,w3,...,wn
b=reg.intercept_#获取截距w0
x0=np.arange(30,60,0.2)
y0=k*x0+b
print("k={0},b={1}".format(k,b))
plt.scatter(x,y)
plt.plot(x0,y0,label='LinearRegression')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()结果:
k=[1.36695374],b=0.13079331831460195
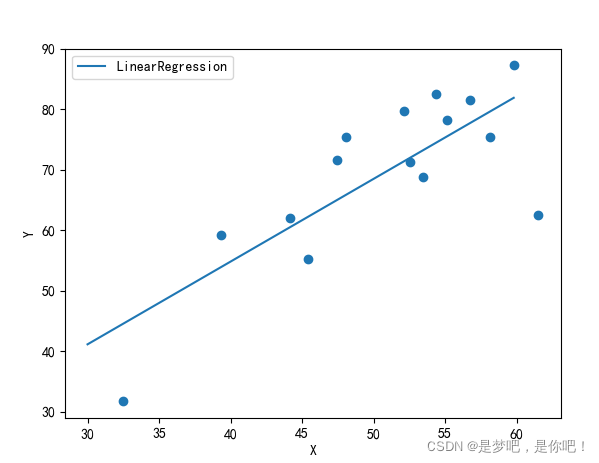
(2)Python详细实现(方法1)

代码:
#方法1
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#数据生成
data = []
for i in range(100):
x = np.random.uniform(3., 12.)
# mean=0, std=1
eps = np.random.normal(0., 1)
y = 1.677 * x + 0.039 + eps
data.append([x, y])
data = np.array(data)
#统计误差
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# computer mean-squared-error
totalError += (y - (w * x + b)) ** 2
# average loss for each point
return totalError / float(len(points))
#计算梯度
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# grad_b = 2(wx+b-y)
b_gradient += (2/N) * ((w_current * x + b_current) - y)
# grad_w = 2(wx+b-y)*x
w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
# update w'
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
#迭代更新
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
b = starting_b
w = starting_w
# update for several times
for i in range(num_iterations):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def main():
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_w = 0 # initial slope guess
num_iterations = 1000
print("迭代前 b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w,
compute_error_for_line_given_points(initial_b, initial_w, data))
)
print("Running...")
[b, w] = gradient_descent_runner(data, initial_b, initial_w, learning_rate, num_iterations)
print("第 {0} 次迭代结果 b = {1}, w = {2}, error = {3}".
format(num_iterations, b, w,
compute_error_for_line_given_points(b, w, data))
)
plt.plot(data[:,0],data[:,1], color='b', marker='+', linestyle='--',label='true')
plt.plot(data[:,0],w*data[:,0]+b,color='r',label='predict')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
if __name__ == '__main__':
main()
结果:
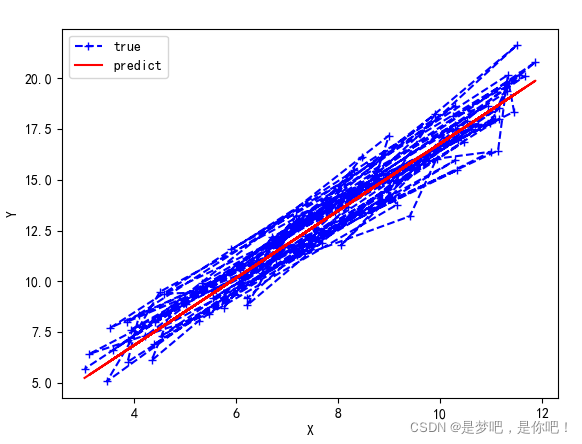
迭代前 :b = 0, w = 0, error = 186.61000821356697
Running...
第 1000 次迭代结果:b = 0.20558501549252192, w = 1.6589067569038516, error = 0.9963685680112963
(3)Python详细实现(方法2)
代码:
#方法2
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# y = wx + b
#Import data
file=pd.read_csv("data.csv")
def compute_error_for_line_given(b, w):
totalError = np.sum((file['y']-(w*file['x']+b))**2)
return np.mean(totalError)
def step_gradient(b_current, w_current, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(file['x']))
for i in range (0,len(file['x'])):
# grad_b = 2(wx+b-y)
b_gradient += (2 / N) * ((w_current * file['x'] + b_current) - file['y'])
# grad_w = 2(wx+b-y)*x
w_gradient += (2 / N) * file['x'] * ((w_current * file['x'] + b_current) - file['x'])
# update w'
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
def gradient_descent_runner( starting_b, starting_w, learning_rate, num_iterations):
b = starting_b
w = starting_w
# update for several times
for i in range(num_iterations):
b, w = step_gradient(b, w, learning_rate)
return [b, w]
def main():
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_w = 0 # initial slope guess
num_iterations = 100
print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w,
compute_error_for_line_given(initial_b, initial_w))
)
print("Running...")
[b, w] = gradient_descent_runner(initial_b, initial_w, learning_rate, num_iterations)
print("After {0} iterations b = {1}, w = {2}, error = {3}".
format(num_iterations, b, w,
compute_error_for_line_given(b, w))
)
plt.plot(file['x'],file['y'],'ro',label='线性回归')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
if __name__ == '__main__':
main()结果:
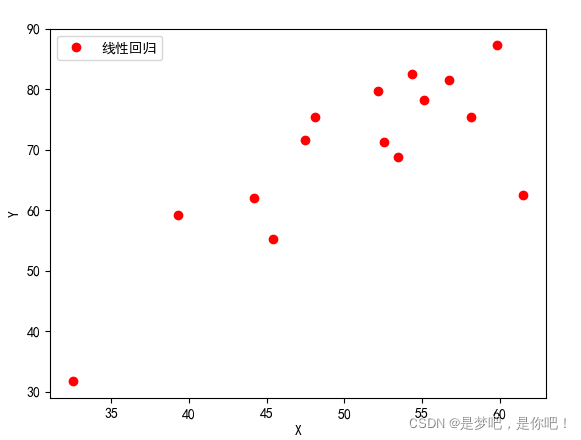
Starting gradient descent at b = 0, w = 0, error = 75104.71822821398 Running... After 100 iterations b = 0 0.014845 1 0.325621 2 0.036883 3 0.502265 4 0.564917 5 0.479366 6 0.568968 7 0.422619 8 0.565073 9 0.393907 10 0.216854 11 0.580750 12 0.379350 13 0.361574 14 0.511651 dtype: float64, w = 0 0.999520 1 0.994006 2 0.999405 3 0.989645 4 0.990683 5 0.991444 6 0.989282 7 0.989573 8 0.988498 9 0.992633 10 0.995329 11 0.989490 12 0.991617 13 0.993872 14 0.991116 dtype: float64, error = 6451.5510231710905
数据:
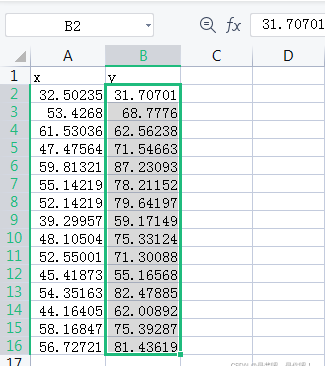
(4)Python详细实现(方法3)
#方法3
import numpy as np
points = np.genfromtxt("data.csv", delimiter=",")
#从数据读入到返回需要两个迭代循环,第一个迭代将文件中每一行转化为一个字符串序列,
#第二个循环迭代对每个字符串序列指定合适的数据类型:
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# computer mean-squared-error
totalError += (y - (w * x + b)) ** 2
# average loss for each point
return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# grad_b = 2(wx+b-y)
b_gradient += (2 / N) * ((w_current * x + b_current) - y)
# grad_w = 2(wx+b-y)*x
w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)
# update w'
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
b = starting_b
w = starting_w
# update for several times
for i in range(num_iterations):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def main():
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_w = 0 # initial slope guess
num_iterations = 1000
print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w,
compute_error_for_line_given_points(initial_b, initial_w, points))
)
print("Running...")
[b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
print("After {0} iterations b = {1}, w = {2}, error = {3}".
format(num_iterations, b, w,
compute_error_for_line_given_points(b, w, points))
)
if __name__ == '__main__':
main()4、案例——房屋与价格、尺寸

(1)代码
#1.导入包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import linear_model
#2.加载训练数据,建立回归方程
# 取数据集(1)
datasets_X = [] #存放房屋面积
datasets_Y = [] #存放交易价格
fr = open('房价与房屋尺寸.csv','r') #读取文件,r: 以只读方式打开文件,w: 打开一个文件只用于写入。
lines = fr.readlines() #一次读取整个文件。
for line in lines: #逐行进行操作,循环遍历所有数据
items = line.strip().split(',') #去除数据文件中的逗号,strip()用于移除字符串头尾指定的字符(默认为空格或换行符)或字符序列。
#split(‘ '): 通过指定分隔符对字符串进行切片,如果参数 num 有指定值,则分隔 num+1 个子字符串。
datasets_X.append(int(items[0])) #将读取的数据转换为int型,并分别写入
datasets_Y.append(int(items[1]))
length = len(datasets_X) #求得datasets_X的长度,即为数据的总数
datasets_X = np.array(datasets_X).reshape([length,1]) #将datasets_X转化为数组,并变为1维,以符合线性回归拟合函数输入参数要求
datasets_Y = np.array(datasets_Y) #将datasets_Y转化为数组
#取数据集(2)
'''fr = pd.read_csv('房价与房屋尺寸.csv',encoding='utf-8')
datasets_X=fr['房屋面积']
datasets_Y=fr['交易价格']'''
minX = min(datasets_X)
maxX = max(datasets_X)
X = np.arange(minX,maxX).reshape([-1,1]) #以数据datasets_X的最大值和最小值为范围,建立等差数列,方便后续画图。
#reshape([-1,1]),转换成1列,reshape([2,-1]):转换成两行
linear = linear_model.LinearRegression() #调用线性回归模块,建立回归方程,拟合数据
linear.fit(datasets_X, datasets_Y)
#3.斜率及截距
print('Coefficients:', linear.coef_) #查看回归方程系数(k)
print('intercept:', linear.intercept_) ##查看回归方程截距(b)
print('y={0}x+{1}'.format(linear.coef_,linear.intercept_)) #拟合线
# 4.图像中显示
plt.scatter(datasets_X, datasets_Y, color = 'red')
plt.plot(X, linear.predict(X), color = 'blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()(2)结果
Coefficients: [0.14198749] intercept: 53.43633899175563 y=[0.14198749]x+53.43633899175563
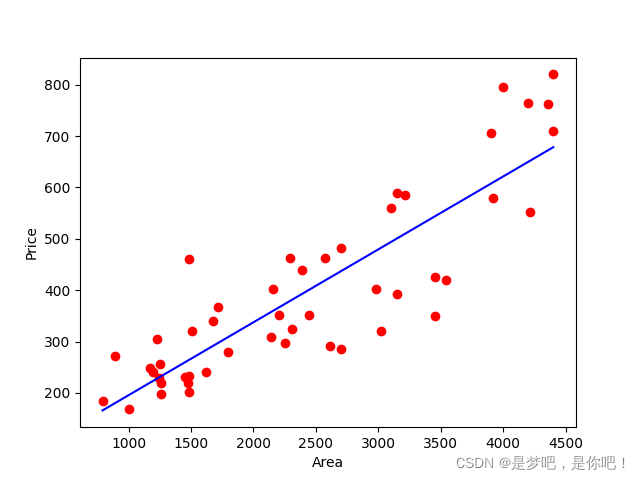
(3)数据
第一列是房屋面积,第二列是交易价格

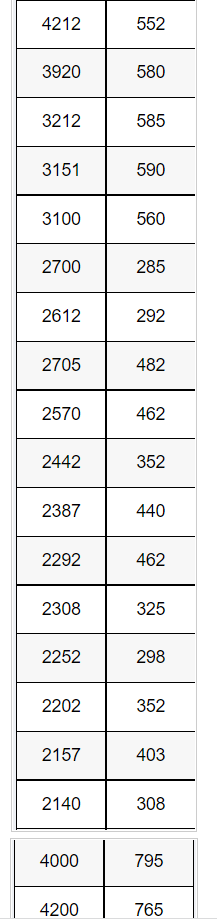
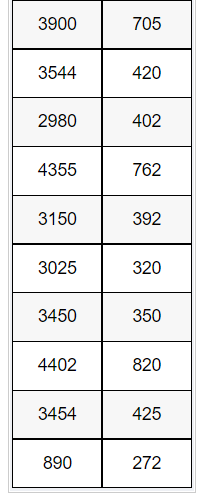
加载全部内容