B+Tree平衡多叉树

InnoDB引擎是通过B+Tree实现索引结构

因为B+Tree是从二叉树演化而来，在这之前我们来先了解二叉树、平衡二叉树、平衡多叉树。

二叉树（Binary Tree）

简介：每个节点最多有两个子树的树结构。
它有一个特点：左子树的键值小于根的键值，右子树的键值大于根的键值。

如下图（图1）所示就是一个二叉树：

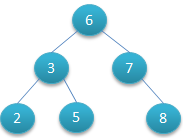
对于该二叉树，假设我们要查找键值为5的节点：

首先从根节点开始，
第一次查找结果为6判断5小于6；
往下查找6的左节点，结果为3判断5大于3；
往下查找3的右节点，结果为5。
一共查找了3次。

我们可以发现：

深度为1的节点需要查找一次，这样的节点有1个需要查找1次；
深度为2的节点需要查找2次，这样的节点有2个共需要查找4次；
深度为3的节点需要查找3次，这样的节点有3个共需要查找9次。
如果要将所有节点全部查找遍历一共需要查找1+4+9=14次。

二叉树可以任意地构造，同样是2、3、5、6、7、8这几个数字，还可以按照下图（图2）的方式构造：

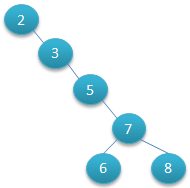
如果要遍历该二叉树所有节点一共需要查找1+2+3+4+5+5=20次，这样效率相对来说就比较低了。
若要最大程度地减少二叉树的查找次数，需要二叉树尽可能地趋近于平衡二叉树。

平衡二叉树（AVL Tree）

简介：在满足二叉树的前提下任一节点上左右两个子树的深度差不超过1。

下面两个二叉树，左边的是平衡二叉树，右边的是非平衡二叉树：

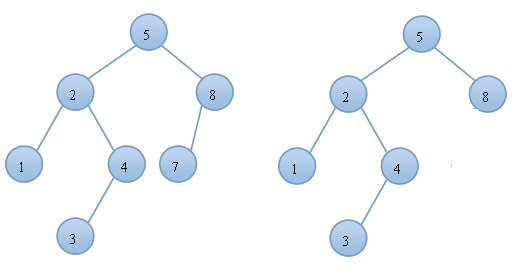
如果在平衡二叉树中插入或删除节点，可能会导致平衡二叉树失衡。
这种失去平衡的二叉树可以概括为四种姿态：LL（左左）、RR（右右）、LR（左右）、RL（右左）。

它们的示意图如下：

这四种失去平衡的姿态都有各自的定义：
LL：LeftLeft，也称“左左”。
插入或删除一个节点后，根节点的左孩子（Left Child）的左孩子（Left Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。
RR：RightRight，也称“右右”。
插入或删除一个节点后，根节点的右孩子（Right Child）的右孩子（Right Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。
LR：LeftRight，也称“左右”。
插入或删除一个节点后，根节点的左孩子（Left Child）的右孩子（Right Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。
RL：RightLeft，也称“右左”。
插入或删除一个节点后，根节点的右孩子（Right Child）的左孩子（Left Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。
平衡二叉树失衡后，可以通过旋转二叉树使其恢复平衡。具体这四种失去平衡姿态情况下对应的旋转方法，请移步BTree和B+Tree详解，里面有十分详细的讲解，这里不再赘述。

平衡多叉树（B-Tree）

B-Tree是为磁盘等设备设计的一种平衡查找树，因此在讲B-Tree之前先了解下磁盘的相关知识。

系统从磁盘读取数据到内存时是以磁盘块（block）为基本单位的，位于同一个磁盘块中的数据会被一次性读取出来，而不是需要什么取什么。

InnoDB存储引擎中有页（Page）的概念，页是其磁盘管理的最小单位。InnoDB存储引擎中默认每个页的大小为16KB，可通过参数innodb_page_size将页的大小设置为4K、8K、16K，
在MySQL中可通过如下命令查看页的大小：

mysql> show variables like 'innodb_page_size';

而系统一个磁盘块的存储空间往往没有这么大，因此InnoDB每次申请磁盘空间时都会是若干个地址连续磁盘块（成为大磁盘块即页，接下来的部分如无特殊说明，所说磁盘块即是InnoDB的页）来达到页的大小16KB。
InnoDB在把磁盘数据读取到内存时会以页为基本单位。

B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。
为了描述B-Tree，首先定义一条记录为一个对象[key, data]，key为记录的键值，对应表中的主键，data为一行记录中除主键外的数据。对于不同的记录，key值互不相同。

m（整数）阶（宽度为m，m>2）B-Tree满足以下条件：

每个节点占用一个磁盘块；
节点（除叶节点外）包含指针、键值（关键字）、数据三种元素，叶节点不包含其它节点的关键字信息：即指针；
所有叶子节点都在同一层；
节点拥有n个按照升序排序的不连续关键字，n在[m/2, m-1]闭区间内为整数；
除叶节点外，n个关键字划分出n+1个范围域对应n+1个指针。指针指向子树关键字的范围域，
比如：以根节点为例，关键字为17和35，p1指针指向的子树的数据范围域小于17，p2指针指向的子树的数据范围域在(17, 35)开区间内，p3指针指向的子树的数据范围域大于35。

见下图：
磁盘块3也是包含三个指针，只是p1和p3的指向磁盘块没有画出来。

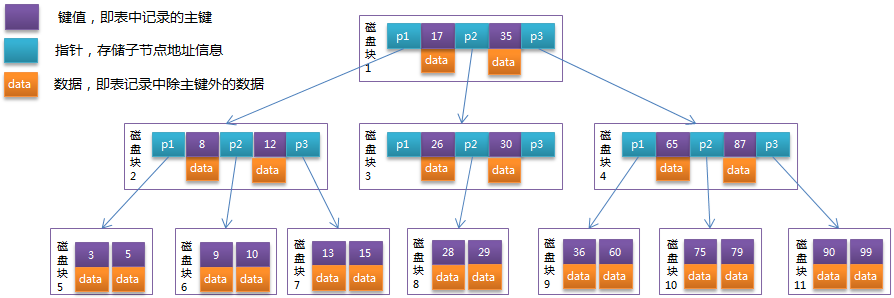
如果要查找关键字29，
那么首先会把磁盘块1由磁盘加载到内存，此时发生一次IO，
在内存中用二分法查找确定29在17和35之间，锁定磁盘块1的P2指针，内存时间因为非常短（相比磁盘的IO）可以忽略不计，
通过磁盘块1的P2指针的磁盘地址把磁盘块3由磁盘加载到内存，发生第二次IO，
29在26和30之间，锁定磁盘块3的P2指针，
通过指针加载磁盘块8到内存，发生第三次IO，
同时内存中做二分查找找到29，结束查询，总计三次IO。

（
基础·磁盘IO与预读：
磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，
这三个部分耗时相加就是一次磁盘IO的时间，大概9ms左右。这个成本是访问内存的十万倍左右；
正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：
预读：每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。
因为局部预读原理说明，当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。
每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。
）

我们再来看二叉树的查找过程

定义一个树高为4的二叉树，查找值为10：

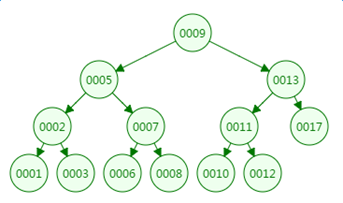
第一次磁盘IO：

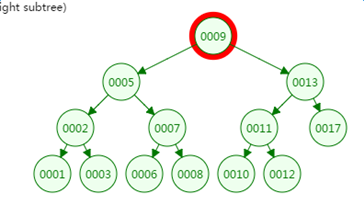
第二次磁盘IO：

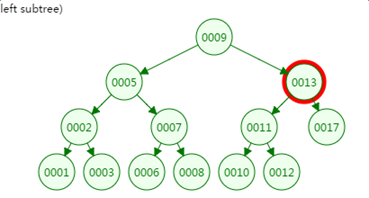
第三次磁盘IO：

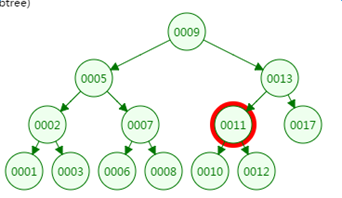
第四次磁盘IO：

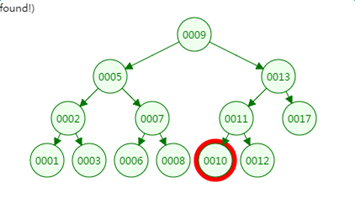
可以看到最坏情况下，磁盘的IO次数等于VAL树的高度。

二叉树深度和节点数的关系：

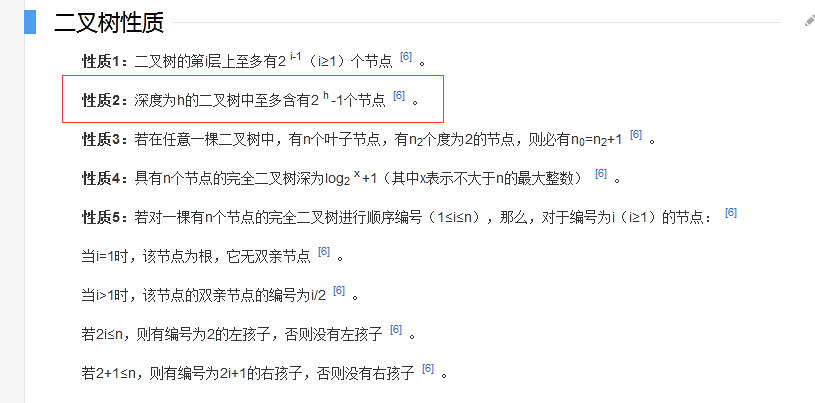
相比VAL二叉树，B-Tree可以大大减少磁盘IO次数。

B+Tree

B+tree是基于B-tree的变体。

B-Tree结构中每个节点中不仅包含数据的key值，还有data值，而每一个节点的存储空间是有限的，
如果data数据比较大会导致每个节点能存储的key的数量变少，导致数据量很大时B-Tree的深度较大，增大查询时的磁盘I/O次数，进而影响查询效率。
在B+Tree中，所有数据记录节点都存放在同一层的叶子节点上，而非叶子节点上只存储key值信息，这样可以大大加大每个节点存储的key值数量，降低B+Tree的高度。

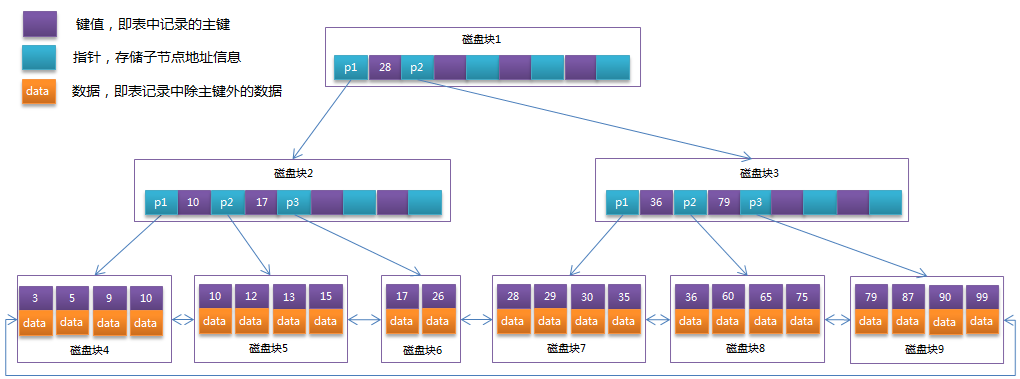
和B-Tree不同，由于它的非叶子节点不存储data信息，所以相同的键值会和data一起，出现在叶子节点中。
以磁盘块3的p2指针为例，指针指向的子树的数据范围域就是在在[36, 79)左开右闭区间内。

InnoDB存储引擎中页的大小为16KB，一般表的主键类型为INT（占用4个字节）或BIGINT（占用8个字节），指针类型也一般为4或8个字节，
一个页（B+Tree中的一个节点）中大概能存储16KB/(8B+8B)=1K个键值（为方便计算，这里的K取值为[10]^3）。
也就是说一个深度为3的B+Tree索引大概可以维护10^3 * 10^3 * 10^3 = 10亿条记录。

实际情况中每个节点可能不能填充满，因此在数据库中，B+Tree的高度一般都在2~4层。
mysql的InnoDB存储引擎在设计时是将根节点常驻内存的，也就是说查找某一键值的行记录时最多只需要1~3次磁盘I/O操作。

聚集和非聚集索引

到这儿，再来理解聚集和非聚集索引就比较简单了。

聚集索引（clustered index）

通常，聚集索引是主键的同义词。一个表中只能拥有一个聚集索引。
聚集索引的逻辑顺序与数据库表中记录在磁盘上的排列顺序一致。通俗来讲就是，聚集索引叶子节点中存储的数据包含表中一条记录完整的信息。找到键值key就找到了整条数据。

非聚集索引（secondary index）

非聚集索引相对来说就不是那么好理解一点。
因为前面我们讲到的关键值key对应的都是数据库中唯一的一条记录，而非聚集索引不一样，它的关键值key无法确定唯一一条记录，多条记录的key值可能会相同。
非聚集索引是通过溢出页来处理这种情况的，当多条记录对应某个同一关键值key时，分配出一个溢出页，
用来存放重复键值及其对应记录的偏移量（该条记录在磁盘上的实际物理位置）。和HashMap解决Hash key冲突类似。
非聚集索引维护了表中记录的逻辑顺序，但是它的叶子节点存储的是表中的记录在数据页中的指针，相比聚集索引会多一次磁盘IO。

以上见解如有不当之处，请予指正。

参考文章：
过来啊小莲：BTree和B+Tree详解
lbcBoy：索引原理-BTree讲解

还有两篇找不到了，找齐之后会在这里补上。

补充参考文章：
SeedQi：B-Tree详解