matlab鸟群算法求解车间调度问题
紫极神光 人气:0一、车间调度简介
1 车间调度定义
车间调度是指根据产品制造的合理需求分配加工车间顺序,从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工。问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次,每个零件都按照一定的顺序进行加工。
2 传统作业车间调度
传统作业车间带调度实例
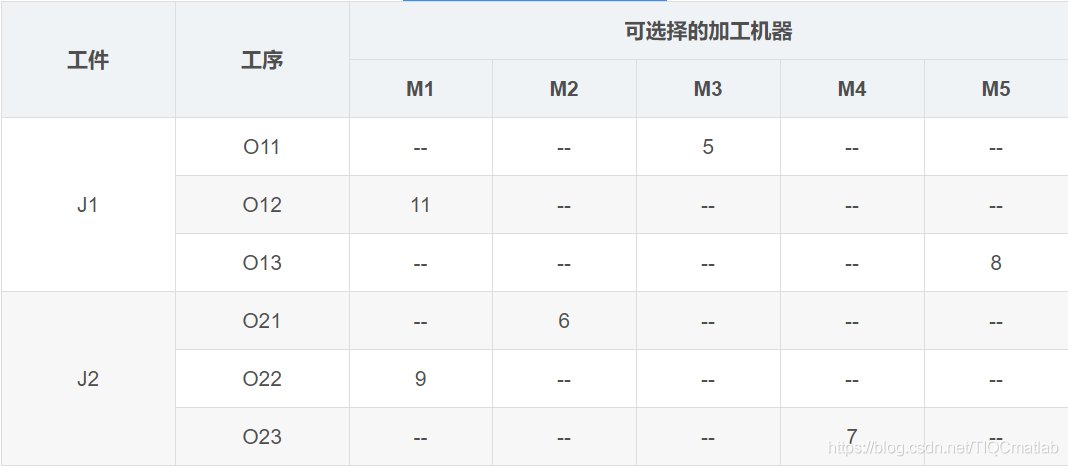
有若干工件,每个工件有若干工序,有多个加工机器,但是每道工序只能在一台机器上加工。对应到上面表格中的实例就是,两个工件,工件J1有三道工序,工序Q11只能在M3上加工,加工时间是5小时。
约束是对于一个工件来说,工序的相对顺序不能变。O11->O12->O13。每时刻,每个工件只能在一台机器上加工;每个机器上只能有一个工件。
调度的任务则是安排出工序的加工顺序,加工顺序确定了,因为每道工序只有一台机器可用,加工的机器也就确定了。
调度的目的是总的完工时间最短(也可以是其他目标)。举个例子,比如确定了O21->O22->O11->O23->O12->O13的加工顺序之后,我们就可以根据加工机器的约束,计算出总的加工时间。
M2加工O21消耗6小时,工件J2当前加工时间6小时。
M1加工O22消耗9小时,工件J2当前加工时间6+9=15小时。
M3加工O11消耗5小时,工件J1当前加工时间5小时。
M4加工O23消耗7小时,工件J2加工时间15+7=22小时。
M1加工O12消耗11小时,但是要等M1加工完O22之后才开始加工O12,所以工件J1的当前加工时间为max(5,9)+11=20小时。
M5加工O13消耗8小时,工件J2加工时间20+8=28小时。
总的完工时间就是max(22,28)=28小时。
3 柔性作业车间调度
柔性作业车间带调度实例(参考自高亮老师论文
《改进遗传算法求解柔性作业车间调度问题》——机械工程学报)
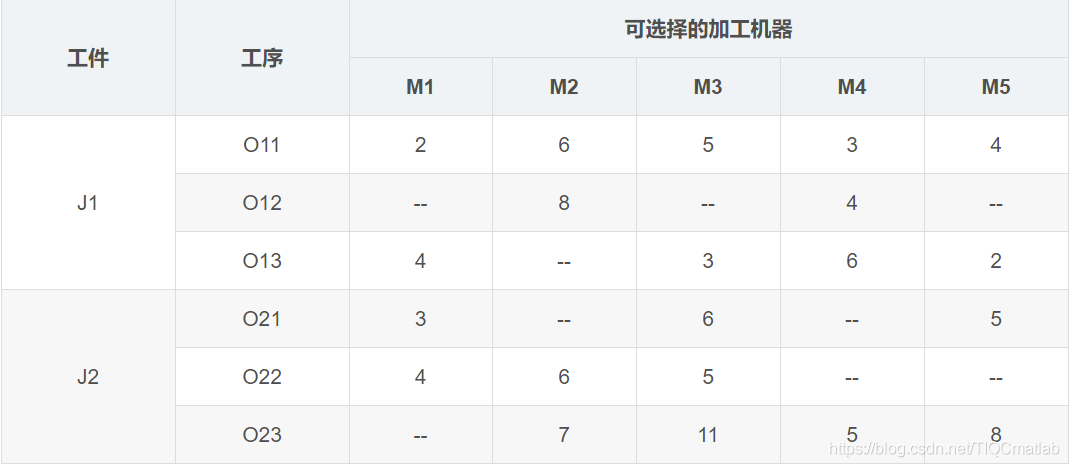
相比于传统作业车间调度,柔性作业车间调度放宽了对加工机器的约束,更符合现实生产情况,每个工序可选加工机器变成了多个,可以由多个加工机器中的一个加工。比如上表中的实例,J1的O12工序可以选择M2和M4加工,加工时间分别是8小时和4小时,但是并不一定选择M4加工,最后得出来的总的完工时间就更短,所以,需要调度算法求解优化。
相比于传统作业车间,柔性车间作业调度的调度任务不仅要确定工序的加工顺序,而且需要确定每道工序的机器分配。比如,确定了O21->O22->O11->O23->O12->O13的加工顺序,我们并不能相应工序的加工机器,所以还应该确定对应的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的机器组合。调度的目的还是总的完工时间最短(也可以是其他目标,比如机器最大负荷最短、总的机器负荷最短)
二、蝴蝶优化算法(MBO)简介
1 介绍
蝴蝶优化算法(butterfly optimization algorithm, BOA)是Arora 等人于2019年提出的一种元启发式智能算法。该算法受到了蝴蝶觅食和交配行为的启发,蝴蝶接收/感知并分析空气中的气味,以确定食物来源/交配伙伴的潜在方向。
蝴蝶利用它们的嗅觉、视觉、味觉、触觉和听觉来寻找食物和伴侣,这些感觉也有助于它们从一个地方迁徙到另一个地方,逃离捕食者并在合适的地方产卵。在所有感觉中,嗅觉是最重要的,它帮助蝴蝶寻找食物(通常是花蜜)。蝴蝶的嗅觉感受器分散在蝴蝶的身体部位,如触角、腿、触须等。这些感受器实际上是蝴蝶体表的神经细胞,被称为化学感受器。它引导蝴蝶寻找最佳的交配对象,以延续强大的遗传基因。雄性蝴蝶能够通过信息素识别雌性蝴蝶,信息素是雌性蝴蝶发出的气味分泌物,会引起特定的反应。
通过观察,发现蝴蝶对这些来源的位置有非常准确的判断。此外,它们可以辨识出不同的香味,并感知它们的强度。蝴蝶会产生与其适应度相关的某种强度的香味,即当蝴蝶从一个位置移动到另一个位置时,它的适应度会相应地变化。当蝴蝶感觉到另一只蝴蝶在这个区域散发出更多的香味时,就会去靠近,这个阶段被称为全局搜索。另外一种情况,当蝴蝶不能感知大于它自己的香味时,它会随机移动,这个阶段称为局部搜索。
2 香味
为了理解BOA中的香味是如何计算的,首先需要理解,像气味、声音、光、温度等这样的模态是如何计算的。感知、处理这些模态需要知道三个重要的术语:感觉模态C、刺激强度I和幂指数a。在感觉模态中,感觉意味着测量能量的形式并以类似方式对其进行处理,而模态是指传感器使用的原始输入。不同的形态可以是气味,声音,光线,温度,在BOA中,模态是香味。I是物理刺激的大小。在BOA中,I与蝴蝶/解决方案的适应度相关。这意味着,当一只蝴蝶散发出更多的香味时,周围的其他蝴蝶可以感知到并被吸引。幂是强度增加的指数。参数a允许正则表达式、线性响应和响应压缩。响应扩展是当I增加时,香味(f)比I增长更快。响应压缩是当I增加时,f比I增长慢。线性响应是当I增加时,f成比例地增加。经实验证明,有时随着刺激的增强,昆虫对刺激变化的敏感性变得越来越低。因此在BOA中,为了估计I的大小,使用了响应压缩。
蝴蝶的自然现象基于两个重要问题:I的变化和f的表示。简单地说,蝴蝶的I与编码后的目标函数相关联。但是,f是相对的,即应该由其他蝴蝶来感知。史蒂文斯幂定律中,为了将气味与其他形式区别开来,使用了C。现在,当I较少的蝴蝶向I较多的蝴蝶移动时,f比I增加得更快。因此,我们应该允许f随幂指数参数a实现的吸收程度而变化。在BOA中,香味被表示为刺激物的物理强度的函数,如下所示:
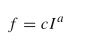
3 具体算法
为了用搜索算法演示上述讨论,将蝴蝶的上述特征理想化如下:
(1)所有的蝴蝶都可以发出气味,这使蝴蝶间相互吸引。
(2)每只蝴蝶都会随机移动或朝最好的蝴蝶移动,散发出更多的芳香。
(3)蝴蝶的刺激强度受目标函数的景观影响或决定。
该算法分为三个阶段:(1)初始化阶段、(2)迭代阶段和(3)结束阶段。
在BOA的每次运行中,首先执行初始化阶段,然后进行迭代搜索,最后在找到最优解时终止算法。BOA中使用的参数值也会被分配,设置这些值后,算法将继续创建初始蝴蝶种群以进行优化。由于在BOA的模拟过程中蝴蝶总数保持不变,分配了一个固定大小的内存来存储信息。蝴蝶的位置是在搜索空间中随机生成的,并计算和存储它们的香味和适应值。这样就完成了初始化阶段,算法开始了迭代阶段,该阶段使用创建的人工蝶形执行搜索。算法的第二阶段,即迭代阶段,由算法执行多次迭代。在每次迭代中,解空间中的所有蝶形都移到新位置,然后重新评估其适应性值。算法首先计算解空间中不同位置的所有蝴蝶的适应度值。那么这些蝴蝶就会利用式1在自己的位置产生香味。该算法有两个关键步骤,即全局搜索阶段和局部搜索阶段。在全局搜索阶段,蝴蝶向最合适的蝴蝶/解g∗迈出一步,该蝴蝶/解g可以用公式(2)来表示。
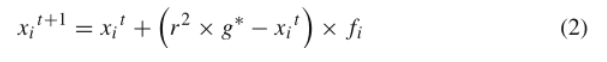
这里,g∗表示在当前迭代的所有解中找到的当前最佳解;fi表示第i只蝴蝶的香味,r是[0,1]中的随机数。局部搜索阶段可以表示为
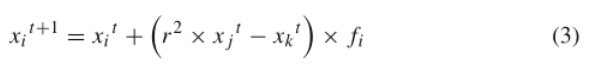
其中,xjt和xkt是解空间中的第j个蝴蝶和第k个蝴蝶。
蝴蝶寻找食物、交配伙伴可以在局部和全局范围内发生。考虑到地理上的接近和各种其他因素,如雨、风等,在整个交配伙伴或蝴蝶的觅食活动中,寻找食物可能占很大比例。因此,在BOA中使用切换概率p来在普通全局搜索和密集局部搜索之间切换。
在未达到停止标准之前,一直进行迭代。迭代结束的标准可以有多个,如使用的最大CPU时间、达到的最大迭代次数、没有改进的最大迭代次数、达到错误率的特定值或任何其他适当的标准。当迭代阶段结束时,算法输出具有最佳适应度的最优解。
三、部分源代码
clc;clear
%% 下载数据
% 加工数据包括加工时间,加工机器,机器数,各机器权重,工件数,各工件对应的工序数
load data operation_time operation_machine num_machine machine_weight num_job num_op
%% 基本参数
MAXGEN=200; % 最大迭代次数
sizepop=201; % 种群规模
e=0.5; % 目标值权重
N_size=30; % 邻域解数量
S_size=15; % 共享解数量
G=5; % 巡回次数
G1=20; % 竞争机制1参数
G2=10; % 竞争机制2参数
trace=zeros(2,MAXGEN);
chrom_best=[];
%% ===========================种群初始化============================
total_op_num=sum(num_op);
chroms=initialization(num_op,num_job,total_op_num,sizepop,operation_machine,operation_time);
[Z,~,~,~,~]=fitness(chroms,num_machine,e,num_job,num_op);
% 将最好的解划分为领飞鸟
[Z_leader,ind]=min(Z);
leader=chroms(ind,:);
% 从chroms中移出领飞鸟,然后划分左右两个跟飞鸟种群
chroms(ind,:)=[];
Z(ind)=[];
sp=(sizepop-1)/2;
lefts=chroms(1:sp,:);
Z_left=Z(1:sp);
rights=chroms(sp+1:end,:);
Z_right=Z(sp+1:end);
%% 候鸟算法中的交叉函数与遗传算法的不同
%% 候鸟算法输入两个染色体种群,分别来自左右队列
%--------------------------------------------------------------------------
function [lefts,Z_left,rights,Z_right]= crossover(lefts,rights,Z_left,Z_right,total_op_num,num_machine,e,num_job,num_op)
chroms1=lefts;
chroms2=rights;
for i=1:size(chroms1,1)
%% 面向工序码的交叉操作
% 父代染色体
parent1=lefts(i,:);
parent2=rights(i,:);
Job=randperm(num_job);
% 将工件随机分成两个集合
J1=Job(1:round(num_job/2));
J2=Job(length(J1)+1:end);
op_p1=[];
op_p2=[];
for j=1:length(J2)
%找出父代中J2片段对应的位置
op_p1=[op_p1,find(parent1(1:total_op_num)==J2(j))];
op_p2=[op_p2,find(parent2(1:total_op_num)==J2(j))];
end
op_s1=sort(op_p1);
op_s2=sort(op_p2);
% 子代1交换J2片段的基因,机器码对应位置的基因,工时码对应位置的基因
chroms1(i,op_s1)=parent2(op_s2);
chroms1(i,total_op_num+op_s1)=parent2(total_op_num+op_s2);
chroms1(i,total_op_num*2+op_s1)=parent2(total_op_num*2+op_s2);
% 子代2同理
chroms2(i,op_s2)=parent1(op_s1);
chroms2(i,total_op_num+op_s2)=parent1(total_op_num+op_s1);
chroms2(i,total_op_num*2+op_s2)=parent1(total_op_num*2+op_s1);
%% 面向机器码的交叉操作
parent1=chroms1(i,:);
parent2=chroms2(i,:);
% 随机产生与染色体长度相等的0,1序列
rand0_1=randi([0,1],1,total_op_num);
for n=1:num_job
ind_0=find(rand0_1(num_op(n)*(n-1)+1:num_op(n)*n)==0);
if ~isempty(ind_0)
ind1=find(parent1(1:total_op_num)==n);
ind2=find(parent2(1:total_op_num)==n);
chroms1(i,total_op_num+ind1(ind_0))=parent2(total_op_num+ind2(ind_0));
chroms1(i,total_op_num*2+ind1(ind_0))=parent2(total_op_num*2+ind2(ind_0));
chroms2(i,total_op_num+ind2(ind_0))=parent1(total_op_num+ind1(ind_0));
chroms2(i,total_op_num*2+ind2(ind_0))=parent1(total_op_num*2+ind1(ind_0));
end
end
end
%% 判断个体是否可以更新
[Z1,~,~,~,~]=fitness(chroms1,num_machine,e,num_job,num_op);
[Z2,~,~,~,~]=fitness(chroms2,num_machine,e,num_job,num_op);
lefts(Z1<Z_left,:)=chroms1(Z1<Z_left,:);
Z_left(Z1<Z_left)=Z1(Z1<Z_left);
rights(Z2<Z_right,:)=chroms2(Z2<Z_right,:);
Z_right(Z2<Z_right)=Z2(Z2<Z_right);
function [Z,makespan,machine_load,machine_weight,pvals] = fitness(chroms,num_machine,e,num_job,num_op)
sizepop=size(chroms,1);
pvals=cell(1,sizepop);
makespan=zeros(1,sizepop);
machine_load=makespan;
total_op_num=sum(num_op); % 总工序数
for k=1:sizepop
chrom=chroms(k,:);
machine=zeros(1,num_machine); % 记录各机器变化时间
job=zeros(1,num_job); % 记录各工件变化时间
machine_time=zeros(1,num_machine); % 计算各机器的实际加工时间
pval=zeros(2,total_op_num); % 记录各工序开始和结束时间
for i=1:total_op_num
else
pval(1,i)=job(chrom(i));
job(chrom(i))=job(chrom(i))+chrom(total_op_num*2+i);
machine(chrom(total_op_num+i))=job(chrom(i));
pval(2,i)=job(chrom(i));
end
machine_time(chrom(total_op_num+i))=machine_time(chrom(total_op_num+i))+chrom(total_op_num*2+i);
end
makespan(k)=max(machine);
machine_weight=machine_time;
machine_load(k)=max(machine_weight)-min(machine_weight);
pvals{k}=pval;
end
Z=e*makespan+(1-e)*machine_load;
四、运行结果
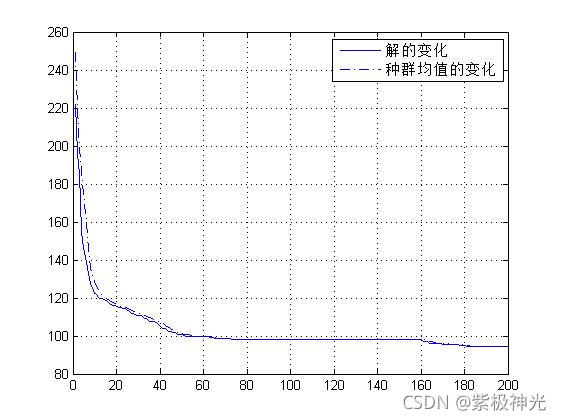
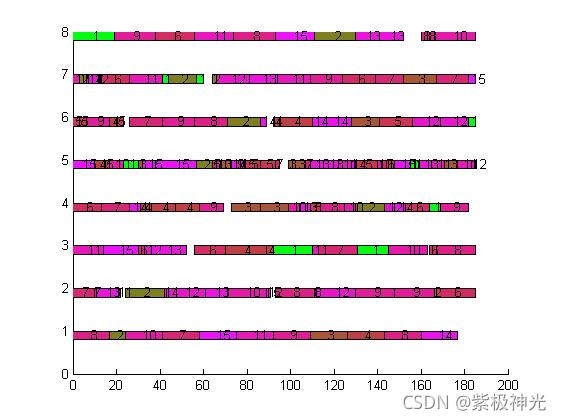

五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]蝴蝶优化算法
加载全部内容