C++马踏棋盘的实现
蜜蜂采蜜 人气:0(一)马踏棋盘经典算法描述:
(1)马踏棋盘是经典的程序设计问题之一,主要的解决方案有两种:一种是基于深度优先搜索的方法,另一种是基于贪婪算法的方法。第一种基于深度优先搜索的方法是比较常用的算法,深度优先搜索算法也是数据结构中的经典算法之一,主要是采用递归的思想,一级一级的寻找,遍历出所有的结果,最后找到合适的解。而基于贪婪的算法则是制定贪心准则,一旦设定不能修改,他只关心局部最优解,但不一定能得到最优解。
【问题描述】关于马踏棋盘的基本过程:国际象棋的棋盘为 8*8 的方格棋盘。现将"马"放在任意指定的方格中,按照"马"走棋的规则将"马"进行移动。要求每个方格只能进入一次,最终使得"马"走遍棋盘的64个方格。
【算法分析】
① 在四角,马踏日走只有两个选择;
② 在其余部分,马踏日走有四、六、八不等的选择。
解决方案:在外层另外加上两层,确保 8*8 方格中的每一个格子都有8中不同的选择;
重点:为了确保每个格子能走日字,而且选择的可能性等同,初始化除了最外两层格子标记没有被访问,最外两层中每个格子都标记为已被访问即可达到目标!
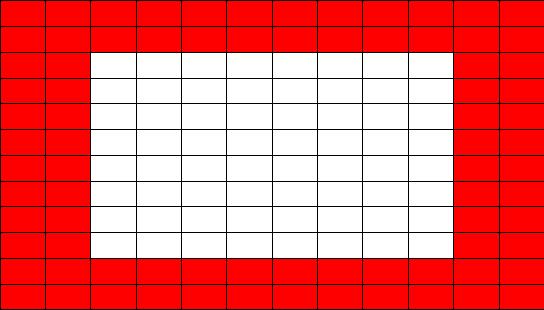
解释:图片中标记红色的区域,初始化时就默认为马已踏日字,集已被访问,而中间的 8*8 的表格标记为马未被访问!
并且每一个表格中马在访问时都有8中不同的选择,这8中不同的选择都会在其相应的x和y坐标上进行追加标记;
这8中选择方式为:

【代码展示1】:递归求解(回溯法求解),列出所有的解,并从中找出从(2,2)位置出发的合适解:
#include <iostream>
#include <stdlib.h>
using namespace std;
int chessboard[12][12] = {0};
int cnt = 0; //标记马已走的方格数
int sum = 0; //标记马走完全程的具体方案数
int move[8][2]={ {2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}}; //初始马当前位置向其周围相邻八个日字的 x,y的偏移量
//输出马踏棋盘的解
void PrintChess();
//马踏棋盘递归过程
void Horse(int x,int y);
int main(void){
int i,j;
for(i=0;i<12;i++){
for(j=0;j<12;j++){
if(i==0 || i==1 || i==10 || i==11 || j==0 || j==1 || j==10 || j==11){
chessboard[i][j]=-1;//在 8 * 8 的外层再加上两层,确保 8 * 8 方格中的每一个格子都有 8 种不同的日字选择
}
}
}
//从起始位置开始求得所有解
chessboard[2][2] = ++cnt;
Horse(2,2); //递归调用当前当前位置附近的 8 个日字,看看是否满足条件
return 0;
}
void Horse(int x,int y){ //马永远踏的是 x,y位置,而不是 a,b
if(cnt >= 64){ //临界值,马走日字全部踏完,成功求出问题解
sum++;
PrintChess();
return;
}
for(int i=0;i<8;i++){
int a = x + move[i][0]; //拿到当前马位置相邻的 8 个日字的 x 坐标
int b = y + move[i][1]; //拿到当前马位置相邻的 8 个日字的 y 坐标
if(chessboard[a][b] == 0){ //判断当前马位置相邻的日字是否已被访问
cnt++;
chessboard[a][b]=cnt; //标志已被访问
Horse(a,b); //从当前马的位置继续往下访问
cnt--;
chessboard[a][b]=0; //回溯回来修改其相邻的日字的访问情况
}
}
}
//输出马踏棋盘的解
void PrintChess(){
cout<<endl<<"马踏棋盘第 "<<sum<<"组解为:"<<endl;
int i,j;
for(i=2;i<10;i++){
for(j=2;j<10;j++){
cout<<" "<<chessboard[i][j];
}
cout<<endl;
}
}
【问题的解】:只列出量两组解,其余未列出:
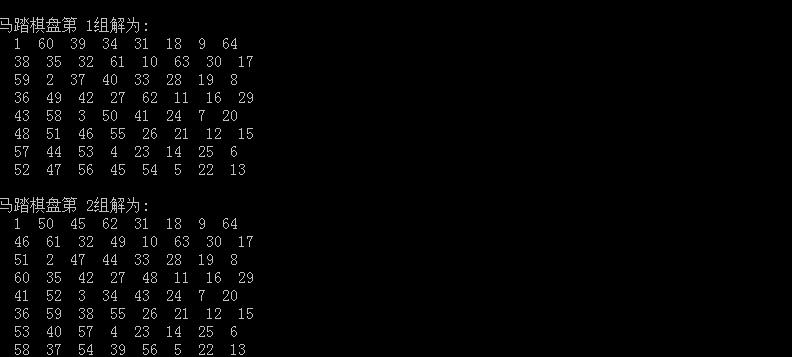
【代码展示2】:贪心算法求解,列出从(2,2)位置出发的合适解,局部最优:
#include <iostream>
#include <stdlib.h>
using namespace std;
/*
typedef struct{
int x; //记录当前马位置的 x 坐标
int y; //记录当前马位置的 y 坐标
int i; //记录从当前马的位置前往下一个日字的序号 i (0<i<8)
}StackHorse;
*/
int StackHorse[100][3]={0}; //申请一个栈空间(里面存储的就是 x,y,i三个具体的变量值),来标记马走的具体位置
int chessboard[12][12] = {0}; //记录 8 * 8棋盘马走的具体脚印
int cnt = 1; //标记马已走的方格数
int move[8][2]={ {2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}}; //初始马当前位置向其周围相邻八个日字的 x,y的偏移量
//输出马踏棋盘的解
void PrintChess();
//马踏棋盘递归过程
void Horse(int x,int y);
int main(void){
int i,j;
for(i=0;i<12;i++){ //初始化马踏棋盘的具体值(0代表未被访问,1代表已被访问,-1代表新加的最外面两层)
for(j=0;j<12;j++){
if(i==0 || i==1 || i==10 || i==11 || j==0 || j==1 || j==10 || j==11){
chessboard[i][j]=-1;
}
}
}
Horse(2,2); //从 (2,2)的位置开始跑,求得马踏棋盘的一组解
PrintChess();
return 0;
}
//非递归求一组解的过程
void Horse(int x,int y){
int top=0,i=0;
int a,b; //记录当前马位置附近的日字坐标
chessboard[x][y]=1; //标记当前起始位置已被访问
StackHorse[top][0]=StackHorse[top][1]=2; //记录当前马的位置
while(cnt < 64){
for(;i<8;i++){
a = x + move[i][0];
b = y + move[i][1];
if(chessboard[a][b] == 0){ //如果当前马位置附近的日字没有被访问
break; //跳出循环
}
}
if(i<8){ //能够访问当前马位置附近的日字
chessboard[a][b]=++cnt;
StackHorse[top][2]=i; //记录访问当前马位置附近的日字序号(0<i<8)
top++; //top指向新的栈顶
StackHorse[top][0]=a; //向新的栈顶放入马踏入的 x坐标
StackHorse[top][1]=b; //向新的栈顶放入马踏入的 y坐标
x=a; //标记新的 x
y=b; //标记新的 y
i=0; //从栈顶马位置开始寻找附近的 8 个日字
}
else{ //没有在当前马位置附近找到符合条件的日字
cnt--; //回溯
chessboard[x][y]=0;
top--; //出栈
x=StackHorse[top][0]; //拿到当前马位置的 x 坐标
y=StackHorse[top][1]; //拿到当前马位置的 y 坐标
i=StackHorse[top][2]; //拿到当前马位置前往下一日字的序号
i++; //继续搜索从当前马位置访问的日字序号的下一位置继续访问
}
}
}
//输出马踏棋盘的解
void PrintChess(){
cout<<"马踏棋盘一组解为:"<<endl;
int i,j;
for(i=2;i<10;i++){
for(j=2;j<10;j++){
cout<<" "<<chessboard[i][j];
}
cout<<endl;
}
}【问题的解】:列出一组解:

加载全部内容