Python 二叉树的概念 Python 二叉树的概念案例详解
Python碎片 人气:0二叉树简介
关于树的介绍,请参考:https:
一、二叉树简介
二叉树是每个节点最多有两个子树的树结构,是一种特殊的树,如下图,就是一棵二叉树。

二叉树是由n(n>=0)个节点组成的数据集合。当 n=0 时,二叉树中没有节点,称为空二叉树。当 n=1 时,二叉树只有根节点一个节点。当 n>1 时,二叉树的每个节点都最多只能有两个子树,递归地构建成一棵完整的二叉树。
二叉树的两个子树被称为左子树(left subtree)和右子树(right subtree)。在二叉树中,如果节点没有子树,则左子树和右子树都为空,如果节点只有一个子树,要根据子树的左右来区分子树是左子树还是右子树,如果节点有两个子树,则左子树和右子树都有。
如果,树中存在一个节点,该节点的子树超过两个,则该树不是二叉树,如下图中,节点C有三个子树,所以这不是一棵二叉树。
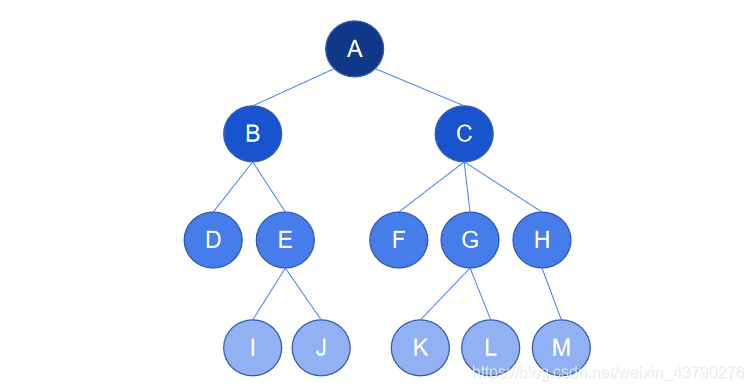
二、几种特殊的二叉树
只要树中所有节点的子树都不超过两个(0个,1个,2个),这就是一棵普通的二叉树。在二叉树中,有一些比较特殊,除了满足二叉树的结构外,还满足一些特殊的规则,主要有如下几种。
1. 完全二叉树:假设一棵二叉树的深度为d(d>1),除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树。
完全二叉树的叶节点只能出现在最下层和次下层,最下层的叶节点靠左紧密地排列,次下层如果存在叶节点,叶节点紧密地靠右排列。
如下图,树的深度为4,除了第4层,节点数达到了最大(“挂满了”),第4层的节点都是紧密地靠左排列(中间没有空位),所以这是一棵完全二叉树。
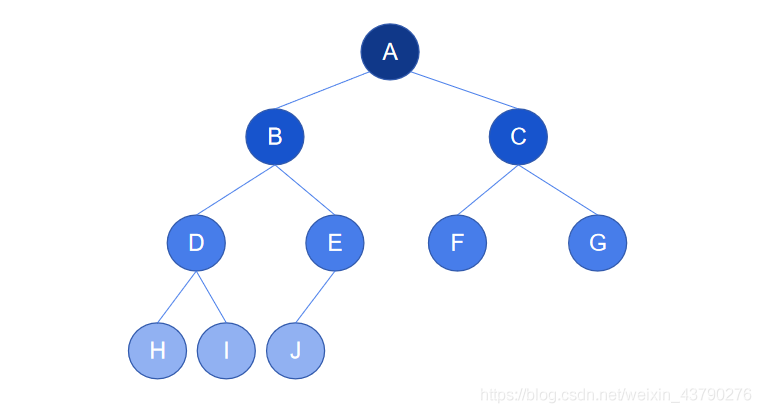
如下图,树的深度也为4,除了第4层,节点数也达到了最大,但是第4层的节点不是紧靠左侧排列的(节点E没有子节点,空了两个位置),所以这不是一棵完全二叉树,只是一棵普通的二叉树。

2. 满二叉树:所有叶节点都在最底层的完全二叉树称为满二叉树。满二叉树是完全二叉树中的特殊情况,除了满足完全二叉树的特征,还满足所有叶节点都在最底层。满二叉树是相同深度的二叉树中叶节点最多的树。
如下图,这首先是一棵完全二叉树,其次,所有的叶节点都在最底层,所以这是一棵满二叉树。其实,满二叉树也可以这么定义,二叉树有节点的所有层,节点数目均已达最大值,则这是一棵满二叉树。

3. 平衡二叉树(AVL树):如果二叉树的所有节点的两棵子树的高度差不大于1,则二叉树被称为平衡二叉树。
如上图中的满二叉树,任何节点的两棵子树高度差都是0(高度都相等,高度差不大于1),所以这是一棵平衡二叉树。
如下图中的二叉树,对于根节点A,左子树是以节点B为根的子树,高度为4,右子树是以节点C为根的子树,高为2,A的左子树与右子树的高度差为2(高度差大于1),所以这不是一棵平衡二叉树。

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,是两人姓的缩写。AVL树中任何节点的两个子树的高度差不大于1,通过高度来判断是否平衡,所以也被称为高度平衡树。
4. 排序二叉树(二叉查找树,Binary Search Tree):又称为二叉搜索树、有序二叉树。
排序二叉树需要具有如下的性质:
4.1 如果二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值。
4.2 如果二叉树的右子树不为空,则右子树上所有节点的值均大于它的根节点的值。
4.3 如果独立地看,左子树、右子树也分别为排序二叉树,用递归的思想,直到树的叶节点。
如下图,根节点8的左子树中,所有节点的值都小于根节点,右子树中,所有节点的值都大于根节点,并且左子树和右子树都是排序二叉树,所以这是一棵排序二叉树。
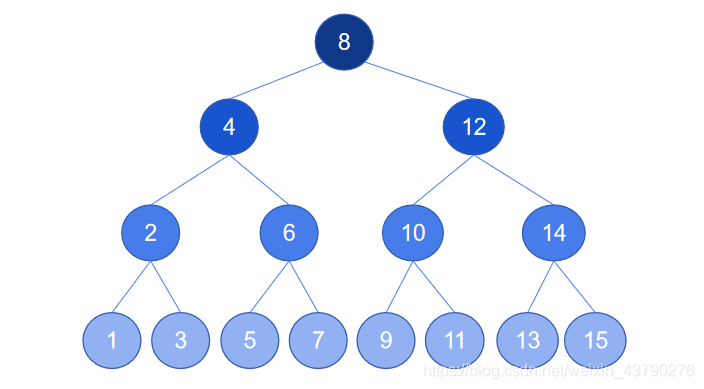
5. 斜树:除了叶节点,所有节点都只有左子树的二叉树称为左斜树。除了叶节点,所有节点都只有右子树的二叉树称为右斜树。他们统称为斜树,判断二叉树是否为斜树,主要是看树的结构,对节点的值没有要求。
如下图,左边的树中,除了叶节点D,所有节点都只有左子树,这是一棵左斜树,同理,右边的树是一棵右斜树。
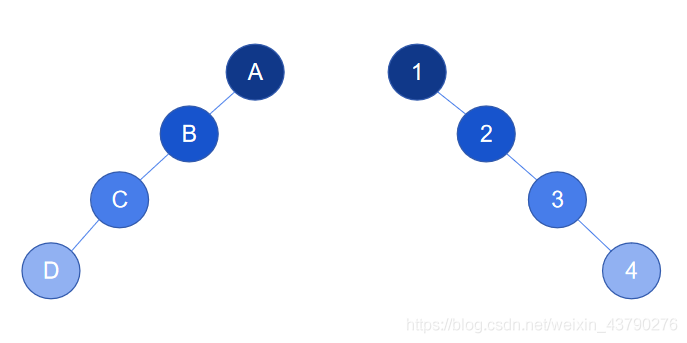
三、二叉树的特点和性质
通过对二叉树的介绍和对几种特殊二叉树的了解,可知二叉树有以下特点:
1. 每个节点最多有两颗子树,所以二叉树中节点的度不大于2,二叉树的度也不会大于2。
2. 左子树和右子树的次序不能颠倒。
3. 即使某节点只有一棵子树,也要根据左右来区分它是左子树还是右子树。
此外,二叉树还具有如下性质:
1. 在二叉树的第i层,至多有 2^(i-1) 个节点(i>0) 。
这里说的是至多的情况,满二叉树的每一层节点都“挂满”了,所以可以用下图中的满二叉树来验证,第1层的节点数为2^(1-1)=1个,... 第4层的节点个数最多为 2^(4-1)=8个。
2. 深度为i的二叉树至多有 2^i - 1 个节点(k>0) 。
这里也是说至多的情况,所以也用满二叉树来验证,深度为4时,二叉树的节点数最多为 2^4 - 1=16-1=15个。

3. 对于任意一棵二叉树,如果其叶节点数为M,度为2的节点总数为N,则 M=N+1 。
为了不失一般性,下图中的树是一棵普通的二叉树,叶节点为 F,H,I,J,K,L ,共6个,度为2的节点为 A,B,C,D,G ,共5个。

4. 具有n个节点的满二叉树的深度必为 log2(n+1) 。这个性质是上面第2点的逆运算。
5. 对于一棵完全二叉树,若从上至下、从左至右编号,则编号为 i 的节点,(叶节点除外)其左子节点的编号必为2i,(叶节点除外)其右子节点的编号必为 2i+1,(根节点除外)其父节点的编号必为i/2(取整除)。
如下图,这是一棵完全二叉树,已经按规则编好号了,可以任意取一个节点进行验证,都是符合此性质的。

加载全部内容