不求甚解的深度学习教程(1)-逻辑回归基本概念以及代价函数

提到深度学习，逻辑回归是最经典的一个例子，也是很多教材的入门算法（比如吴恩达的深度学习）。鉴于本人零基础学习人工智能的痛苦经历，所以用通俗的语言把逻辑回归讲清楚。深度学习本身核心知识是数学知识，涉及到线性代数、概率论，微积分等。体会到很多读者都是像我一样，已经把这些知识早就还给老师了，所以我会逐步完善这个系列，用尽量通俗的语言来把深度学习的知识分享整理一遍。

什么是“逻辑”？什么是“回归”？

逻辑回归，英文名logistics regression，虽然带了“逻辑”二字，但是和逻辑没有任何关系，它是一种对样本进行分类的方式。比如是否是垃圾邮件、是否患某种疾病，是解决二分类问题的一个方式，所以结果要么是0，要么是1。想一下，我们学计算机时那个课程是主要和0、1打交道？当然是逻辑运算那一块！所以这么理解逻辑。

那为什么又叫“回归”呢？刚才举的例子里明明是个分类问题，为什么取名“回归”呢（回归在我们中国人思维定式里，就是香港回归、澳门回归）？查看维基百科的解释：

回归分析是建立因变量 Y {\displaystyle Y} Y（或称依变量，反因变量）与自变量 X {\displaystyle X} X（或称独变量，解释变量）之间关系的模型

　　看图，用人话解释一下，就是知道了很多点（蓝色）的X坐标和Y坐标，找到一条线来最大可能的符合这些点的趋势，也就是我们初中学的线性方程。

 所以，什么是逻辑回归呢？就是通过提供的一些数据，找到一个函数，来匹配这些数据的分类关系。

这和我们曾经学习数据的思维方式不一样，过去我们数学一直学习y=f(x)=ax+b之类，如y=x+1，很明显a=1，b=2，通过此求解x或者y的值。现在反过来来了，知道很多x和y的值（如图上的点），来求解a、b的值。人工智能、机器学习的大部分算法都是在寻找一个最优的a、b等参数的值。

如何找到a、b两个参数的值？先找一个预测的函数

刚才我们提到，逻辑回归的最终分类结果只有0和1两个结果，所以对应上文提到的所有的采样点x，所有的y值只能有0或者1两个结果。所以刚才的坐标系曲线应该是如下图

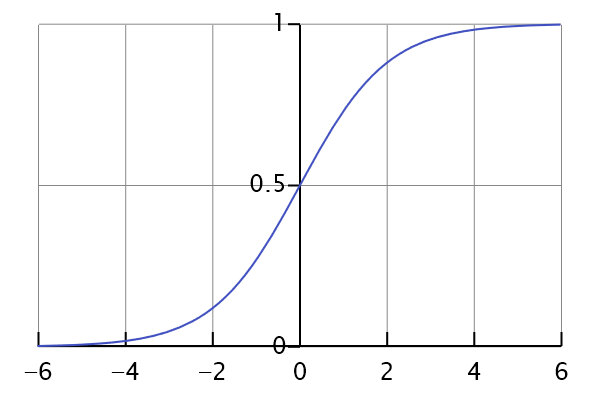
那如何把之前f(x)=ax+b对应到上面这个图上呢（最终取值是0或者1）？还好数学家们帮我们找到了一个函数，名叫Sigmoid函数，机器学习里名字叫激活函数。为什么叫激活函数，我们以后再解释。

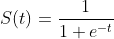
这个函数形状如它的名字“S”，正好符合上面0~1的曲线。把t换成原来的ax+b，就得到下面的公式

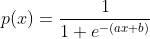
 所以接下来我们就围绕这个公式做研究，怎么找到a、b的值。

预测的函数和真实函数的差距

有一点一定要注意：当前这个p(x)函数是我们推测、假定的函数，是极度接近真实数据的函数。但是他和理想中的函数有有一定差距的，也就是误差。所以换句话说，和真实结果做下下对比，我们把误差计算出来，找到误差最小的时候，是不是就找到一个最接近真实函数的预测函数，从而就找到a、b的理论值了？

所以我们先看看误差函数怎么定义

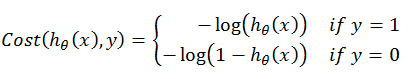
hθ(x)：用参数θ和x预测出来的y值；这是一个新的符号，一定要注意。
y：原训练样本中的y值，也就是标准答案；

虽然这个函数英文名cost一看就明白，专业名词叫损失函数，但是很多人一看就头大，为什么用这个函数。。。这个得问数学老师，反正通过这个函数，我们能正好完美的算出真实值和预测值的差。详细解释，利用高中数学知识

1. 当y=1的时候，Cost(h(x), y) = -log(h(x))。h(x)的值域0~1，-log(h(x))的曲线图，如下

【字很小，但是很重要^_^】

h(x)的值趋近于1的时候，代价函数的值越小趋近于0，也就是说预测的值h(x)和训练集结果y=1越接近，预测错误的代价越来越接近于0，分类结果为1的概率为1
当h(x)的值趋近于0的时候，代价函数的值无穷大，也就说预测的值h(x)和训练集结果y=1越相反，预测错误的代价越来越趋于无穷大，分类结果为1的概率为0

2. 当y=0的时候， Cost(h(x), y) = -log(1-h(x))。h(x)的值域0~1，-log(1-h(x))的曲线图，如下

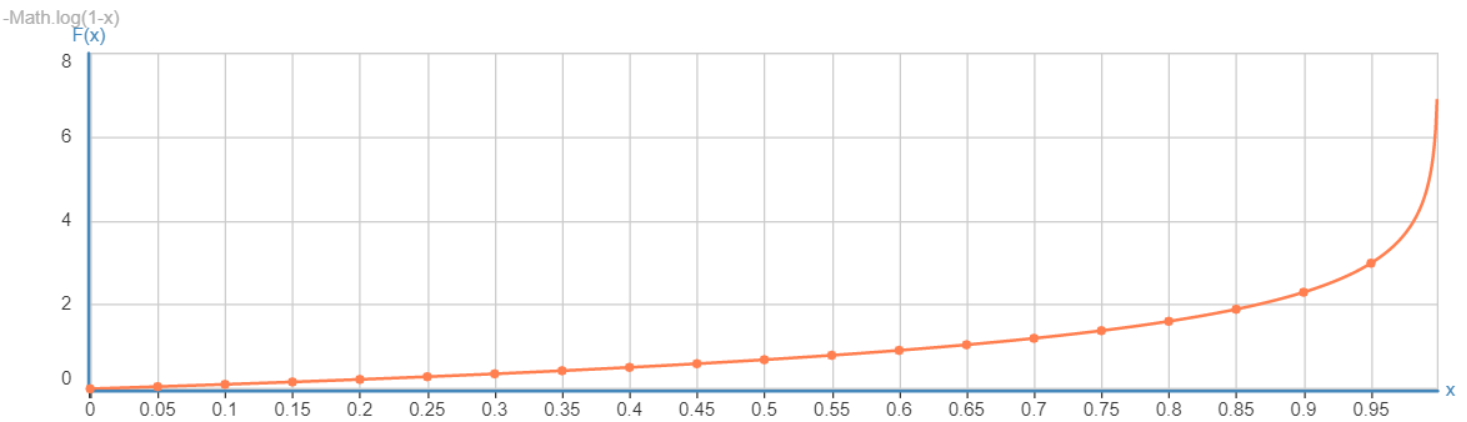
 【字很小，但是很重要^_^】

h(x)的值趋近于1的时候，代价函数的值趋于无穷大，也就是说预测的值h(x)和训练集结果y=0越相反，预测错误的代价越来越趋于无穷大，分类结果为0的概率为1-h(x)等于0
当h(x)的值趋近于0的时候，代价函数的值越小趋近于0，也就说预测的值h(x)和训练集结果y=0越接近，预测错误的代价越来越接近于0，分类结果为0的概率为1-h(x)等于1

为了统一表示，可以把Cost(h(x), y)表达成统一的式子，根据前面J(θ)的定义，扩展到所有m个样本，J(θ)等于

特别说明:
1. 当y=1的时候，第二项(1-y)log(1-h(x))等于0
2. 当y=0的时候，ylog(h(x))等于0
3. m指的是现在有m个点的y值需要与预测值进行比较

所以，我们是不是找到这个函数的最小值就找到a、b的值了？接下来一篇文章我们会讲如何通过高中学的导数知识来求解这个最小值。

---------------------------------------------

上文都是自己在学习过程中的一些总结，后续欢迎加qq群595560901交流