前言

前面介绍了基本图形、模型、曲线的绘制，但是，在好像还没有感受到那种3D游戏里一些能惊艳到自己的效果，即真实感还不是很足。这篇文章中介绍的光线追踪，是实现真实感必不可少的。拿下面的两张图片来对比

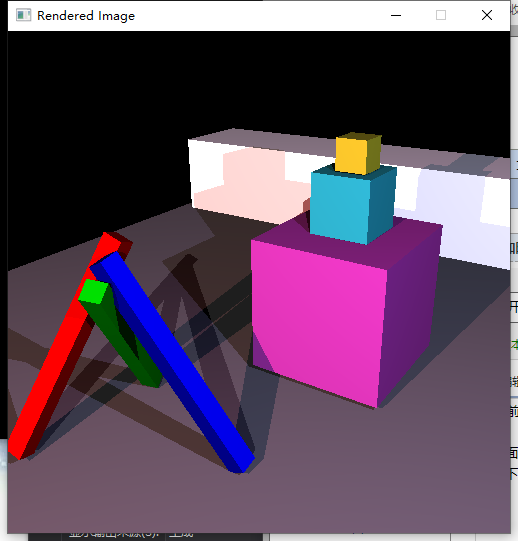
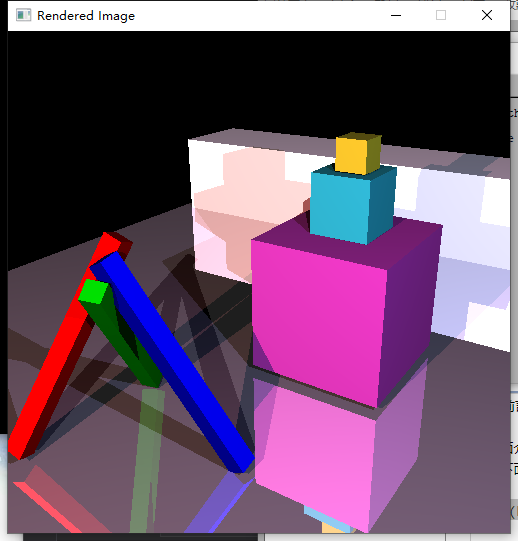
对比一下是不是被下面这张图片的效果惊艳到了？可以很明显感觉到，下面的这个图片效果要好的多。这篇博客将介绍如何实现这样的效果。

光线求交

这里暂时只介绍光线与球面和三角面片的求交

光线与球面相交

射线的方程：
\[ R(t) = A+tD \]
球面的隐式方程：
\[ (X-C)^2=r^2 \]
联立两式：
\[ (A+tD-C)^2=r^2 \]
然后通过判别式：\[\Delta=4[(A-C) \cdot D]^2 - 4(A-C)^2+r^2\]来判断是否相交。

交点法向量：
\[ N=\frac{P-C}{||P-C||} \]

bool Sphere::intersectLocal( const ray& r, isect& i ) const
{
    // YOUR CODE HERE:
    // 光线与球面相交
    // Add sphere intersection code here.
    Vec3d A = r.getPosition();
    Vec3d D = r.getDirection();
    Vec3d C= Vec3<double>();
    double _r = 1.0;
    double a = D.length2();
    double b = 2 * (A - C) * D;
    double c = (A - C).length2() - _r;
    double delta = b * b - 4 * a * c;
    // it currently ignores all spheres and just return false.
    if (delta >= 0) {
        double t1 = (-b + sqrt(delta)) / (2 * a);
        double t2 = (-b - sqrt(delta)) / (2 * a);
        if (t1 <= RAY_EPSILON)
            return false;
        else {
            double t;
            if (t2 <= RAY_EPSILON) {
                t = t1;
                i.outsideTheObject = false;
            }
            else {
                t = t2;
                i.outsideTheObject = true;
            }
            // 焦点设置
            i.obj = this;
            i.setT(t);
            Vec3d P = r.at(t);
            Vec3d Normal = P;
            if (D*Normal > 0)
                Normal = -Normal;
            Normal.normalize();
            i.setN(Normal);
            return true;
        }
    }
    return false;
}

光线与三角面片相交

射线的方程：
\[ R(t) = A+tD \]
三角面片点法式方程：
\[ N(p-p_1)=0 \]
联立两式得：
\[ t=\frac{N\cdot p_1 - N \cdot A}{n\cdot D} \]
求出t后，便得到交点坐标，然后可通过同向法来判别交点是否在平面内。

// Calculates and returns the normal of the triangle too.
bool TrimeshFace::intersectLocal(const ray& r, isect& i) const
{
    // YOUR CODE HERE:
    // Add triangle intersection code here.
    // it currently ignores all triangles and just return false.
    //
    // Note that you are only intersecting a single triangle, and the vertices
    // of the triangle are supplied to you by the trimesh class.
    //
    // You should retrieve the vertices using code like this:
    //
    // const Vec3d& a = parent->vertices[ids[0]];
    // const Vec3d& b = parent->vertices[ids[1]];
    // const Vec3d& c = parent->vertices[ids[2]];
    const Vec3d& a = parent->vertices[ids[0]];
    const Vec3d& b = parent->vertices[ids[1]];
    const Vec3d& c = parent->vertices[ids[2]];

    Vec3d edge1 = b - a;
    Vec3d edge2 = c - a;
    // 计算平面法向量
    Vec3d nor = edge1 ^ edge2;
    nor.normalize();

    // 判断是否与平面平行
    float x = nor * r.getDirection();
    if (x == 0)
        return false;
    // Ax + By + Cz = d
    float d = nor * a;
    float t = (d - nor * r.getPosition()) / x;
    if (t <= RAY_EPSILON)
        return false;
    Vec3d intersection_point = r.at(t);
    Vec3d edge3 = intersection_point - a;
    // 同向法判断是否在平面内
    if (((b - a) ^ (intersection_point - a)) * nor <= 0)
        return false;
    else if (((c - b) ^ (intersection_point - b)) * nor <= 0)
        return false;
    else if (((a - c) ^ (intersection_point - c)) * nor <= 0)
        return false;
    else {
        //交点设置
        i.obj = this;
        i.setT(t);
        i.setN(nor);
        return true;
    }

}

当然，这里还可以使用重心坐标法来实现

光线衰减

在现实场景中，光线也是会衰减的，比如看同一场景，距离远近不同看到的清晰度也就不同，这是距离衰减。还有阴影衰减，当有物体遮挡住部分光的时候，会形成一定的阴影，这就是阴影衰减产生的效果。

距离衰减

点光源：
\[ A_{j}^{d i s t}=\min \left\{1, \frac{1}{a_{j}+b_{j} r_{j}+c_{j} r_{j}^{2}}\right\} \]

double PointLight::distanceAttenuation( const Vec3d& P ) const
{
    // You'll need to modify this method to attenuate the intensity 
    // of the light based on the distance between the source and the 
    // point P.  For now, we assume no attenuation and just return 1.0
    Vec3d d = P - position;
    double r = d.length(); //距离
    return min(1.0, 1.0 / (constantTerm + linearTerm * r + quadraticTerm * r*r));
//  return 1.0;
}

平行光源：

double DirectionalLight::distanceAttenuation( const Vec3d& P ) const
{
    // distance to light is infinite, so f(di) goes to 0.  Return 1.
    return 1.0;
}

阴影衰减

点光源：

首先判断光线是否被遮挡，然后再判断是否超出光强所能打到的距离

Vec3d PointLight::shadowAttenuation(const Vec3d& P) const
{
    // YOUR CODE HERE:
    // You should implement shadow-handling code here.
    Vec3d d = getDirection(P);
    isect i;
    ray shadowRay(P, d);
    if (this->getScene()->intersect(shadowRay, i)) {
        double tLight = (P - position).length();
        if (i.t < tLight)
            return Vec3d(0, 0, 0);
        else
            return Vec3d(1, 1, 1);
    }
    return Vec3d(1,1,1);
}

平行光：

只需判断是否被遮挡即可

Vec3d DirectionalLight::shadowAttenuation( const Vec3d& P ) const
{
    // YOUR CODE HERE:
    Vec3d d = getDirection(P);
    isect i;
    ray shadowRay(P, d);
    if (this->getScene()->intersect(shadowRay, i)) {
        return Vec3d(0, 0, 0);
    }
    // You should implement shadow-handling code here.
    return Vec3d(1,1,1);
}

光线追踪

先来份伪代码

光线跟踪中的四种射线：

• 视线：由视点与象素(x，y)发出的射线

• 阴影测试线：物体表面上点与光源的连线

• 反射光线

• 折射光线

光线追踪的过程

phong光照模型

由物体表面上一点P反射到视点的光强I为环境光的反射光强\(I_e\)、理想漫反射光强\(I_d\)、和镜面反射光\(I_s\)的总和，即
\[ I=I_ak_a + I_lk_d(L \cdot N)+k_s\sum_{i=1}^{m}[I_{pi}(R \cdot V)^n] \]
在washington CSE 457的课件中给出的公式为
\[ l_{\text {direct }}=k_{e}+k_{e} I_{L s}+\sum_{f} A_{j}^{\text {shadow}} A_{j}^{\text {dist}} I_{L j} B_{j}\left[k_{d}\left(\mathbf{N} \cdot \mathbf{L}_{j}\right)+k_{s}\left(\mathbf{N} \cdot \mathbf{H}_{j}\right)^{n_{s}}\right] \]
其中\(k_d\)项表示漫反射，采用Lamber模型，\(k_s\)项表示镜面反射
\[ I_{d}=I_{p} K_{d} *(L \cdot N) \]

\[ I_{s}=k_{s} I_{p}(R \cdot V)^{n} \]

即可写出下列代码

// Apply the Phong model to this point on the surface of the object, returning
// the color of that point.
Vec3d Material::shade( Scene *scene, const ray& r, const isect& i ) const
{
    // YOUR CODE HERE

    // For now, this method just returns the diffuse color of the object.
    // This gives a single matte color for every distinct surface in the
    // scene, and that's it.  Simple, but enough to get you started.
    // (It's also inconsistent with the Phong model...)

    // Your mission is to fill in this method with the rest of the phong
    // shading model, including the contributions of all the light sources.
    // You will need to call both distanceAttenuation() and shadowAttenuation()
    // somewhere in your code in order to compute shadows and light falloff.
    if( debugMode )
        std::cout << "Debugging the Phong code (or lack thereof...)" << std::endl;

    Vec3d pos = r.at(i.t);
    Vec3d N = i.N;  
    N.normalize();
    Vec3d Ip, L, H, Atten;
    Vec3d shadow = ke(i) + prod(scene->ambient(), ka(i));
    for (vector<Light*>::const_iterator litr = scene->beginLights();
        litr != scene->endLights(); ++litr) {
        Light* pLight = *litr;
        Ip = pLight->getColor(pos);
        L = pLight->getDirection(pos);
        H = -r.getDirection() + L;  H.normalize();
        Atten = pLight->distanceAttenuation(pos)*pLight->shadowAttenuation(pos);
        shadow += prod(Atten, prod(Ip, kd(i)*(L*N) + ks(i)*pow(H*N, 256)));
    }
    return shadow;
}

反射方向

这里的反射指的是镜面反射

计算公式：
\[ R=2(V\cdot N)N-V \]
为什么是这样呢？首先来看\(V\cdot N\)，这里N是交点处的法向量，并且是单位向量，那个即视线在法向量上的投影，再乘法向量的两倍，得到的是平行四边形的对角线，减去V便是反射后的光线的方向。

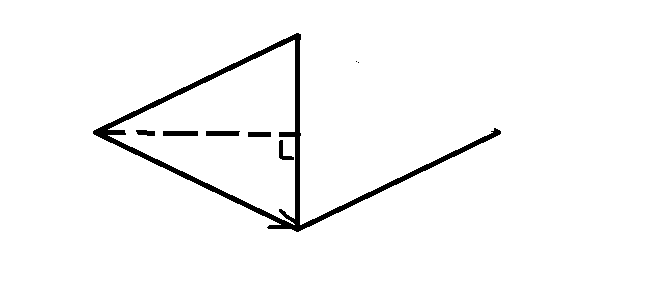
折射方向

跟反射方向一样都是公式推导
\[ \begin{array}{l}{\eta=\frac{\eta_{i}}{\eta_{t}}} \\ \eta_{i} \sin \theta_{i}=\eta_{t} \sin \theta_{t} \\ {\cos \theta_{i}=\mathbf{N} \cdot \mathbf{V}} \\ {\cos \theta_{t}=\sqrt{1-\eta^{2}\left(1-\cos ^{2} \theta_{i}\right)}} \\ {\mathbf{T}=\left(\eta \cos \theta_{i}-\cos \theta_{t}\right) \mathbf{N}-\eta \mathbf{V}}\end{array} \]

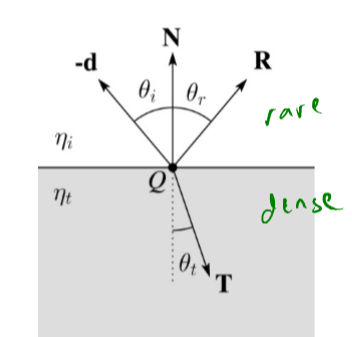
终止条件

经过上述的介绍，很容易可以想到，什么时候终止光线追踪

• 该光线未碰到任何物体

• 该光线碰到了背景

• 光线在经过许多次反射和折射以后，就会产生衰减，光线对于视点的光强贡献很小（小于某个设定值）。

• 光线反射或折射次数即跟踪深度大于一定值

因此，光线追踪的代码实现如下

// Do recursive ray tracing!  You'll want to insert a lot of code here
// (or places called from here) to handle reflection, refraction, etc etc.
Vec3d RayTracer::traceRay( const ray& r, 
    const Vec3d& thresh, int depth )
{
    isect i;

    if( scene->intersect( r, i ) && depth >= 0) {
        const Material& m = i.getMaterial();

        //计算光源直射
        Vec3d I = m.shade(scene, r, i);

        //计算反射递归
        Vec3d Q = r.at(i.t);
        Vec3d R = r.getDirection() - 2 * (r.getDirection()*i.N)*i.N;
        R.normalize();
        I += prod(m.kr(i), traceRay(ray(Q, R), thresh, depth - 1));

        //计算折射递归
        double cosThetaI = -i.N*r.getDirection();
        double eta = (i.outsideTheObject) ? 1.0003 / m.index(i) : m.index(i) / 1.0003;
        if (eta*eta*(1 - cosThetaI * cosThetaI) < 1) {
            double cosThetaT = sqrt(1 - eta * eta*(1 - cosThetaI * cosThetaI));
            Vec3d T = (eta*cosThetaI - cosThetaT)*i.N - eta * r.getDirection();
            T.normalize();
            I += prod(m.kt(i), traceRay(ray(Q, -T), thresh, depth - 1));
        }
        return I;
        // An intersection occured!  We've got work to do.  For now,
        // this code gets the material for the surface that was intersected,
        // and asks that material to provide a color for the ray.  

        // This is a great place to insert code for recursive ray tracing.
        // Instead of just returning the result of shade(), add some
        // more steps: add in the contributions from reflected and refracted
        // rays.

        //const Material& m = i.getMaterial();
        //return m.shade(scene, r, i);
    
    } else {
        // No intersection.  This ray travels to infinity, so we color
        // it according to the background color, which in this (simple) case
        // is just black.

        return Vec3d( 0.0, 0.0, 0.0 );
    }
}

小节

到这里，光线追踪也就差不多介绍完了，这一系列博客也算是收尾了。那天在课上听其他同学展示的的时候，说是我的世界有部分的开源源码，里面有一个可以实现光追的接口，有兴趣的小伙伴可以去康康，似乎那个仅仅实现光追还无法达到很好的效果，还要加上路线追踪，emmmmm。。。。期末考完有空了我再去康康，明早图形学考试祝我好运 orz