[ch04-05] 梯度下降的三种形式
五弦木头 人气:6系列博客,原文在笔者所维护的github上:https://aka.ms/beginnerAI,
点击star加星不要吝啬,星越多笔者越努力。
4.5 梯度下降的三种形式
我们比较一下目前我们用三种方法得到的w和b的值,见表4-2。
表4-2 三种方法的结果比较
| 方法 | w | b |
|---|---|---|
| 最小二乘法 | 2.056827 | 2.965434 |
| 梯度下降法 | 1.71629006 | 3.19684087 |
| 神经网络法 | 1.71629006 | 3.19684087 |
这个问题的原始值是可能是\(w=2,b=3\),由于样本噪音的存在,使用最小二乘法得到了2.05、2.96这样的非整数解,这是完全可以接受的。但是使用梯度下降和神经网络两种方式,都得到1.71、3.19这样的值,准确程度很低。从图4-6的神经网络的训练结果来看,拟合直线是斜着穿过样本点区域的,并没有在正中央的骨架上。
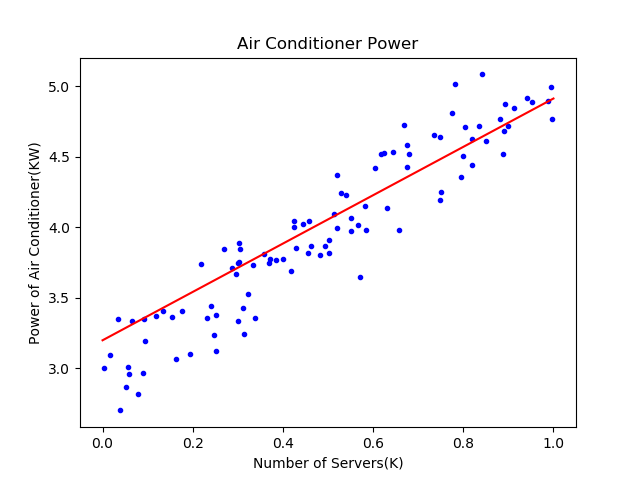
图4-6 拟合效果
难度是神经网络方法有什么问题吗?
初次使用神经网络,一定有水土不服的地方。最小二乘法可以得到数学解析解,所以它的结果是可信的。梯度下降法和神经网络法实际是一回事儿,只是梯度下降没有使用神经元模型而已。所以,接下来我们研究一下如何调整神经网络的训练过程,先从最简单的梯度下降的三种形式说起。
在下面的说明中,我们使用如下假设,以便简化问题易于理解:
- 使用可以解决本章的问题的线性回归模型,即\(z=x \cdot w+b\)
- 样本特征值数量为1,即\(x、w、b\)都是标量
- 使用均方差损失函数。
计算w的梯度:
\[ {\partial{loss} \over \partial{w}} = \frac{\partial{loss}}{\partial{z_i}}\frac{\partial{z_i}}{\partial{w}}=(z_i-y_i)x_i \]
计算b的梯度:
\[ \frac{\partial{loss}}{\partial{b}} = \frac{\partial{loss}}{\partial{z_i}}\frac{\partial{z_i}}{\partial{b}}=z_i-y_i \]
4.5.1 单样本随机梯度下降
SDG(Stochastic Grident Descent)
样本访问示意图如图4-7所示。

图4-7 单样本访问方式
计算过程
假设一共100个样本,每次使用1个样本:
\(repeat\{ \\\)
\(\quad for \quad i=1,2,3,...,100\{ \\\)
\(\quad \quad z_i = x_i \cdot w + b\\\)
\(\quad \quad dw= x_i \cdot (z_i - y_i)\\\)
\(\quad \quad db= z_i - y_i \\\)
\(\quad \quad w=w-\eta \cdot dw \\\)
\(\quad \quad db=b-\eta \cdot db \\\)
\(\quad\} \\\)
\(\}\)
特点
- 训练样本:每次使用一个样本数据进行一次训练,更新一次梯度,重复以上过程。
- 优点:训练开始时损失值下降很快,随机性大,找到最优解的可能性大。
- 缺点:受单个样本的影响最大,损失函数值波动大,到后期徘徊不前,在最优解附近震荡。不能并行计算。
运行结果
设置batch_size=1,即单样本方式:
if __name__ == '__main__':
sdr = SimpleDataReader()
sdr.ReadData()
params = HyperParameters(1, 1, eta=0.1, max_epoch=100, batch_size=1, eps = 0.02)
net = NeuralNet(params)
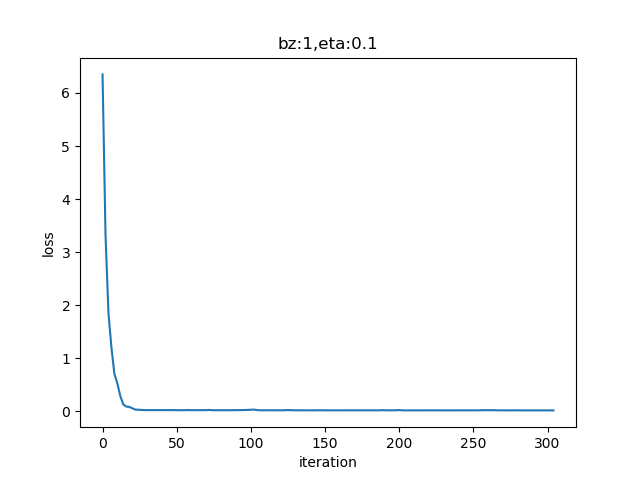
net.train(sdr)表4-3 单样本方式的训练情况
| 损失函数值 | 梯度下降过程 |
|---|---|
 |
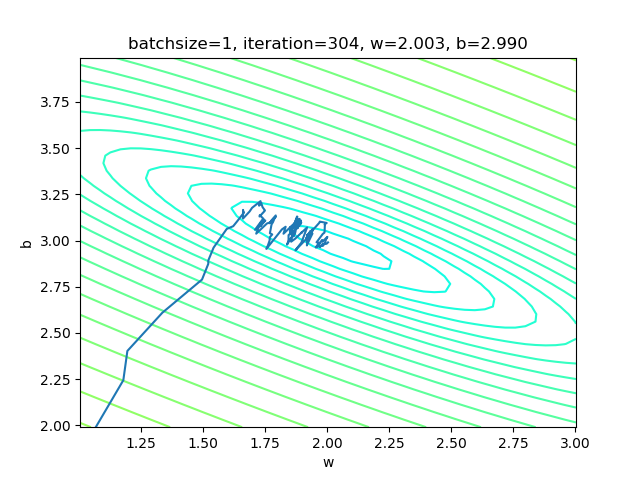 |
表4-3的左图,由于我们使用了限定的停止条件,即当损失函数值小于等于0.02时停止训练,所以,单样本方式迭代了300次后达到了精度要求。
右图是w和b共同构成的损失函数等高线图。梯度下降时,开始收敛较快,稍微有些弯曲地向中央地带靠近。到后期波动较大,找不到准确的前进方向,曲折地达到中心附近。
4.5.2 小批量样本梯度下降
Mini-Batch Gradient Descent
样本访问示意图如图4-8所示。

图4-8 小批量样本访问方式
计算过程
假设一共100个样本,每个小批量5个样本:
\(repeat\{ \\\)
\(\quad for \quad i=1,6,11,...,96\{\\\)
\(\quad \quad z_i = x_i \cdot w + b \\\)
\(\quad \quad z_{i+1} = x_{i+1} \cdot w + b \\\)
\(\quad \quad \dots \\\)
\(\quad \quad z_{i+4} = x_{i+4} \cdot w + b \\\)
\(\quad \quad dw= {1 \over 5}\sum_{k=i}^{i+4} x_k \cdot (z_k - y_k) \\\)
\(\quad \quad db= {1 \over 5}\sum_{k=i}^{i+4} (z_k - y_k) \\\)
\(\quad \quad w=w-\eta \cdot dw \\\)
\(\quad \quad db=b-\eta \cdot db \\\)
\(\quad\}\\\)
\(\}\)
上述算法中,循环体中的前5行分别计算了\(z_i, z_{i+1}, ..., z_{i+4}\),可以换成一次性的矩阵运算。
特点
- 训练样本:选择一小部分样本进行训练,更新一次梯度,然后再选取另外一小部分样本进行训练,再更新一次梯度。
- 优点:不受单样本噪声影响,训练速度较快。
- 缺点:batch size的数值选择很关键,会影响训练结果。
运行结果
设置batch_size=10:
if __name__ == '__main__':
sdr = SimpleDataReader()
sdr.ReadData()
params = HyperParameters(1, 1, eta=0.3, max_epoch=100, batch_size=10, eps = 0.02)
net = NeuralNet(params)
net.train(sdr) 表4-4 小批量样本方式的训练情况
| 损失函数值 | 梯度下降过程 |
|---|---|
 |
 |
表4-4的右图,梯度下降时,在接近中心时有小波动。图太小看不清楚,可以用matplot工具放大局部来观察。和单样本方式比较,在中心区的波动已经缓解了很多。
小批量的大小通常由以下几个因素决定:
- 更大的批量会计算更精确的梯度,但是回报却是小于线性的。
- 极小批量通常难以充分利用多核架构。这决定了最小批量的数值,低于这个值的小批量处理不会减少计算时间。
- 如果批量处理中的所有样本可以并行地处理,那么内存消耗和批量大小成正比。对于多硬件设施,这是批量大小的限制因素。
- 某些硬件上使用特定大小的数组时,运行时间会更少,尤其是GPU,通常使用2的幂数作为批量大小可以更快,如32 ~ 256,大模型时尝试用16。
- 可能是由于小批量在学习过程中加入了噪声,会带来一些正则化的效果。泛化误差通常在批量大小为1时最好。因为梯度估计的高方差,小批量使用较小的学习率,以保持稳定性,但是降低学习率会使迭代次数增加。
在实际工程中,我们通常使用小批量梯度下降形式。
4.5.3 全批量样本梯度下降
Full Batch Gradient Descent
样本访问示意图如图4-9所示。

图4-9 全批量样本访问方式
计算过程
假设一共100个样本,每次使用全部样本:
\(repeat\{ \\\)
\(\quad z_1 = x_1 \cdot w + b \\\)
\(\quad z_2 = x_2 \cdot w + b \\\)
\(\quad \dots \\\)
\(\quad z_{100} = x_{100} \cdot w + b \\\)
\(\quad dw= {1 \over 100}\sum_{i=1}^{100} x_i \cdot (z_i - y_i) \\\)
\(\quad db= {1 \over 100}\sum_{i=1}^{100} (z_i - y_i) \\\)
\(\quad w=w-\eta \cdot dw \\\)
\(\quad db=b-\eta \cdot db \\\)
\(\}\)
上述算法中,循环体中的前100行分别计算了\(z_1, z_2, ..., z_{100}\),可以换成一次性的矩阵运算。
特点
- 训练样本:每次使用全部数据集进行一次训练,更新一次梯度,重复以上过程。
- 优点:受单个样本的影响最小,一次计算全体样本速度快,损失函数值没有波动,到达最优点平稳。方便并行计算。
- 缺点:数据量较大时不能实现(内存限制),训练过程变慢。初始值不同,可能导致获得局部最优解,并非全局最优解。
运行结果
if __name__ == '__main__':
sdr = SimpleDataReader()
sdr.ReadData()
params = HyperParameters(1, 1, eta=0.5, max_epoch=1000, batch_size=-1, eps = 0.02)
net = NeuralNet(params)
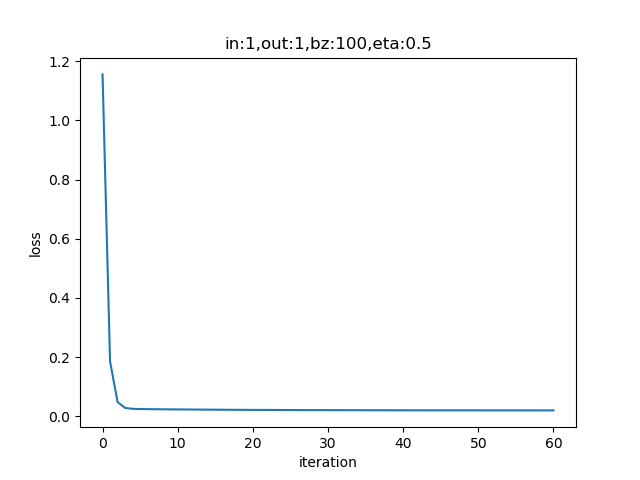
net.train(sdr)设置batch_size=-1,即是全批量的意思。
表4-5 全批量样本方式的训练情况
| 损失函数值 | 梯度下降过程 |
|---|---|
 |
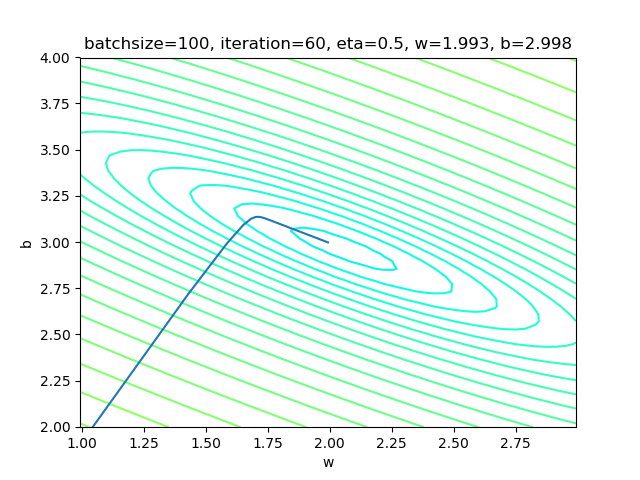 |
表4-5中的右图,梯度下降时,在整个过程中只拐了一个弯儿,就直接到达了中心点。
4.5.4 三种方式的比较
表4-6 三种方式的比较
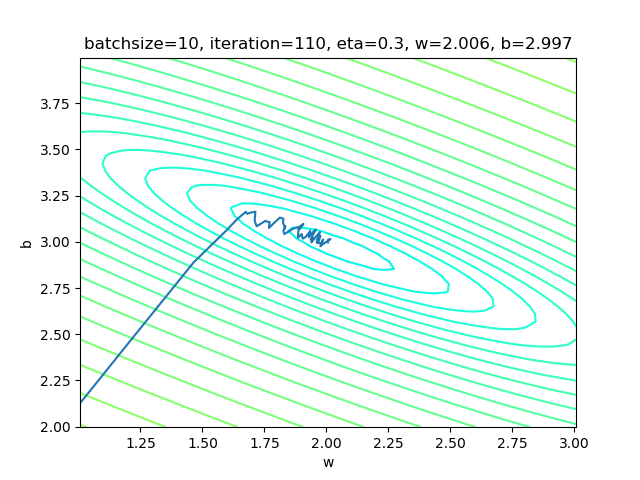
| 单样本 | 小批量 | 全批量 | |
|---|---|---|---|
| 梯度下降过程图解 |  |
 |
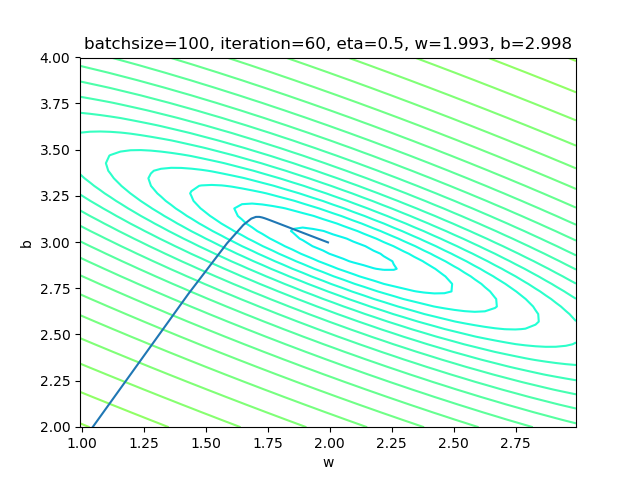 |
| 批大小 | 1 | 10 | 100 |
| 学习率 | 0.1 | 0.3 | 0.5 |
| 迭代次数 | 304 | 110 | 60 |
| epoch | 3 | 10 | 60 |
| 结果 | w=2.003, b=2.990 | w=2.006, b=2.997 | w=1.993, b=2.998 |
表4-6比较了三种方式的结果,从结果看,都接近于\(w=2,b=3\)的原始解。最后的可视化结果图如图4-10,可以看到直线已经处于样本点比较中间的位置。
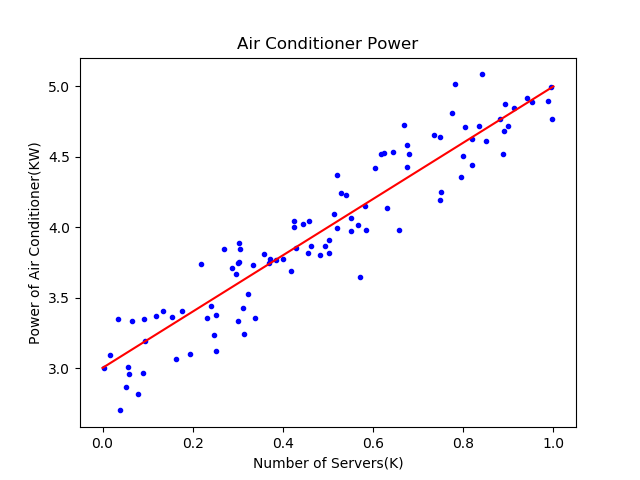
图4-10 较理想的拟合效果图
相关的概念:
- Batch Size:批大小,一次训练的样本数量。
- Iteration:迭代,一次正向 + 一次反向。
- Epoch:所有样本被使用了一次,叫做一个Epoch,中文的翻译比较杂乱,所以干脆就用原文比较清楚。
假设一共有样本1000个,batch size=20,则一个Epoch中,需要1000/20=50次Iteration才能训练完所有样本。
代码位置
ch04, Level5
思考与练习
- 调整学习率、批大小等参数,观察神经网络训练的过程与结果
- 进一步提高精度(设置eps为更小的值),观察w和b的结果值以及拟合直线的位置
- 用纸笔推算一下矩阵运算的维度。假设:
- X (4x2)
- W (2x3)
- B (1x3)
加载全部内容