Python优化算法之遗传算法案例代码
旅途中的宽~ 人气:0一、前言
优化算法,尤其是启发式的仿生智能算法在最近很火,它适用于解决管理学,运筹学,统计学里面的一些优化问题。比如线性规划,整数规划,动态规划,非线性约束规划,甚至是超参数搜索等等方向的问题。
但是一般的优化算法还是matlab里面用的多,Python相关代码较少。
我在参考了一些文章的代码和模块之后,决定学习scikit-opt这个模块。这个优化算法模块对新手很友好,代码简洁,上手简单。而且代码和官方文档是中国人写的,还有很多案例,学起来就没什么压力。
缺点是包装的算法种类目前还不算多,只有七种:(差分进化算法、遗传算法、粒子群算法、模拟退火算法、蚁群算法、鱼群算法、免疫优化算法)
本次带来的是数学建模里面经常使用的遗传算法的使用演示。
二、安装
首先安装模块,在cmd里面或者anaconda prompt里面输入:
pip install scikit-opt
对于当前开发人员版本:
git clone git@github.com:guofei9987/scikit-opt.git cd scikit-opt pip install .
三、遗传算法
3.1 自定义函数
UDF(用户定义函数)现已推出!
例如,您刚刚制定了一种新型函数。现在,你的函数是这样的:

该函数有大量的局部最小值,具有很强的冲击力,在(0,0) 处的全局最小值,值为 0。
import numpy as np
def schaffer(p):
x1, x2 = p
x = np.square(x1) + np.square(x2)
return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)导入和构建 ga :(遗传算法)
from sko.GA import GA
ga = GA(func=schaffer, n_dim = 2, size_pop = 100, max_iter = 800, prob_mut = 0.001, lb = [-1, -1], ub = [1, 1], precision = 1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)运行结果为:

可以看到基本找到了全局最小值和对应的x 。
画出迭代次数的图:
import pandas as pd import matplotlib.pyplot as plt Y_history = pd.DataFrame(ga.all_history_Y) fig, ax = plt.subplots(2, 1) ax[0].plot(Y_history.index, Y_history.values, '.', color = 'red') Y_history.min(axis = 1).cummin().plot(kind = 'line') plt.show()
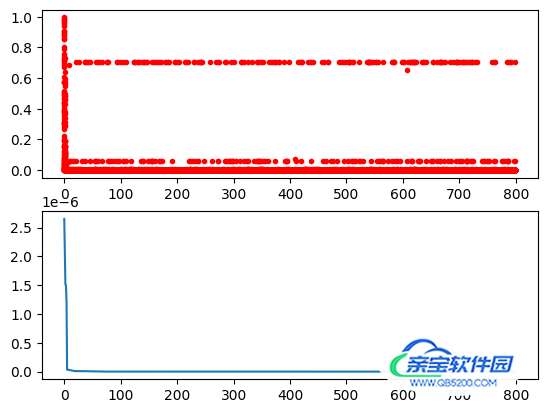
GA算法的参数详解:
输入参数:
| 输入参数 | 默认值 | 参数的意义 |
|---|---|---|
| func | - | 目标函数 |
| n_dim | - | 目标函数的维度 |
| size_pop | 50 | 种群规模 |
| max_iter | 200 | 最大迭代次数 |
| prob_mut | 0.001 | 变异概率 |
| lb | -1 | 每个自变量的最小值 |
| ub | 1 | 每个自变量的最大值 |
| constraint_eq | 空元组 | 等式约束 |
| constraint_ueq | 空元组 | 不等式约束 |
| precision | 1e-7 | 精确度,int / float或者它们组成的列表 |
输出参数:
GA & GA_TSP
| 输出参数 | 参数的意义 |
|---|---|
| ga.generation_best_X | 每一代的最优函数值对应的输入值 |
| ga.generation_best_Y | 每一代的最优函数值 |
| ga.all_history_FitV | 每一代的每个个体的适应度 |
| ga.all_history_Y | 每一代每个个体的函数值 |
3.2 遗传算法进行整数规划
在多维优化时,想让哪个变量限制为整数,就设定 precision 为 整数 即可。
例如,我想让我的自定义函数的某些变量限制为整数+浮点数(分别是整数,整数,浮点数),那么就设定 precision=[1, 1, 1e-7]
例子如下:
from sko.GA import GA
demo_func = lambda x: (x[0] - 1) ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2
ga = GA(func = demo_func, n_dim = 3, max_iter = 500, lb = [-1, -1, -1], ub = [5, 1, 1], precision = [1,1,1e-7])
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
可以看到第一个、第二个变量都是整数,第三个就是浮点数了 。
3.3 遗传算法用于旅行商问题
商旅问题(TSP)就是路径规划的问题,比如有很多城市,你都要跑一遍,那么先去哪个城市再去哪个城市可以让你的总路程最小。
实际问题需要一个城市坐标数据,比如你的出发点位置为(0,0),第一个城市离位置为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),第二个为 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)…这里没有实际数据,就直接随机生成了。
import numpy as np from scipy import spatial import matplotlib.pyplot as plt num_points = 50 points_coordinate = np.random.rand(num_points, 2) # generate coordinate of points points_coordinate
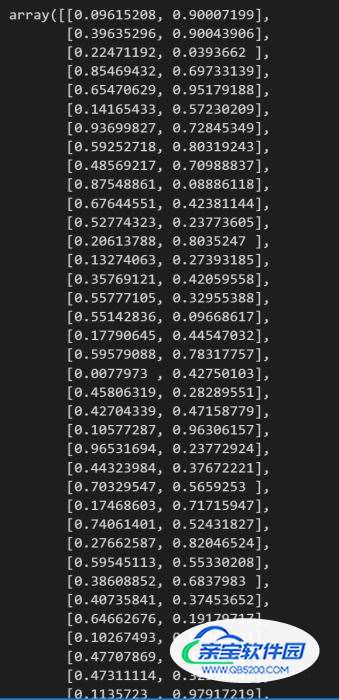
这里定义的是50个城市,每个城市的坐标都在是上图随机生成的矩阵。
然后我们把它变成类似相关系数里面的矩阵:
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean') distance_matrix.shape
(50, 50)
这个矩阵就能得出每个城市之间的距离,算上自己和自己的距离(0),总共有2500个数。
定义问题:
def cal_total_distance(routine):
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])求解问题:
from sko.GA import GA_TSP ga_tsp = GA_TSP(func = cal_total_distance, n_dim = num_points, size_pop = 50, max_iter = 500, prob_mut = 1) best_points, best_distance = ga_tsp.run()
我们展示一下结果:
best_distance

画图查看计算出来的路径,还有迭代次数和y的关系:
fig, ax = plt.subplots(1, 2,figsize = (12, 8)) best_points_ = np.concatenate([best_points, [best_points[0]]]) best_points_coordinate = points_coordinate[best_points_, :] ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r') ax[1].plot(ga_tsp.generation_best_Y) plt.show()
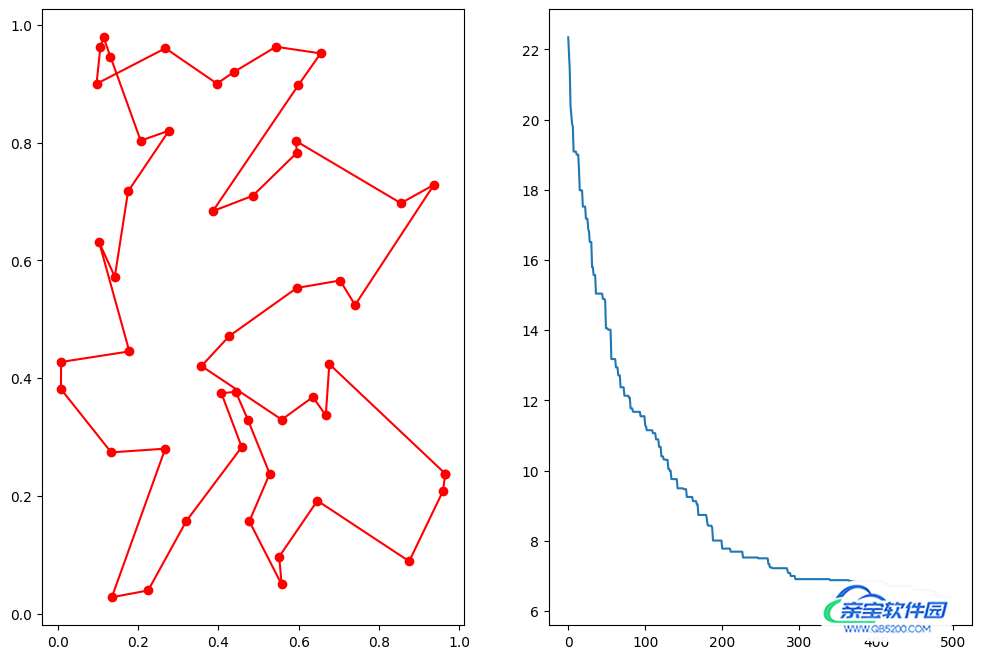
3.4 使用遗传算法进行曲线拟合
构建数据集:
import numpy as np import matplotlib.pyplot as plt from sko.GA import GA x_true = np.linspace(-1.2, 1.2, 30) y_true = x_true ** 3 - x_true + 0.4 * np.random.rand(30) plt.plot(x_true, y_true, 'o')
构建的数据是 y = x 3 − x + 0.4 y=x^3-x+0.4 y=x3−x+0.4,然后加上了随机扰动项。如图:

定义需要拟合的函数(三次函数),然后将残差作为目标函数去求解:
def f_fun(x, a, b, c, d):
return a * x ** 3 + b * x ** 2 + c * x + d #三次函数
def obj_fun(p):
a, b, c, d = p
residuals = np.square(f_fun(x_true, a, b, c, d) - y_true).sum()
return residuals求解:
ga = GA(func = obj_fun, n_dim = 4, size_pop = 100, max_iter = 500, lb = [-2] * 4, ub = [2] * 4)
best_params, residuals = ga.run()
print('best_x:', best_params, '\n', 'best_y:', residuals)
可以看到拟合出来的方程为 y = 0.9656 x 3 − 0.0065 x 2 − 1.0162 x + 0.2162 y=0.9656x^{3}-0.0065x^{2}-1.0162x+0.2162 y=0.9656x3−0.0065x2−1.0162x+0.2162
画出拟合线:
y_predict = f_fun(x_true, *best_params) fig, ax = plt.subplots() ax.plot(x_true, y_true, 'o') ax.plot(x_true, y_predict, '-') plt.show()
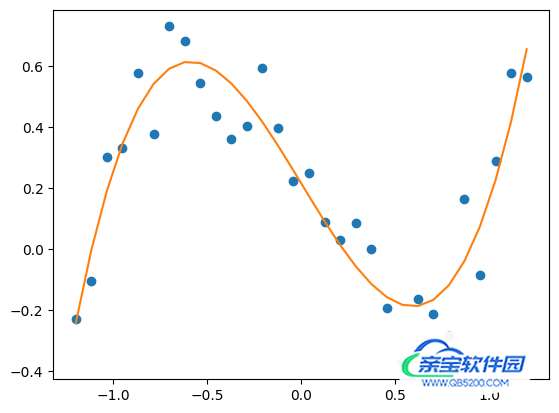
加载全部内容