C/C++浮点数使用的两个注意事项详解

时间:2023-03-20 摆烂小青菜人气:0

一.回顾浮点数的存储与读取

浮点数的存入与读取流程总览：

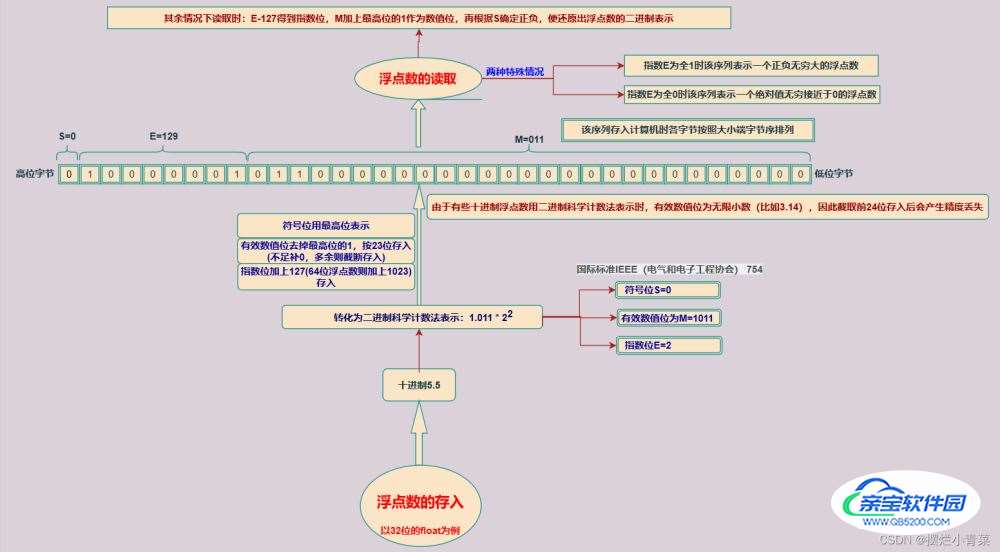
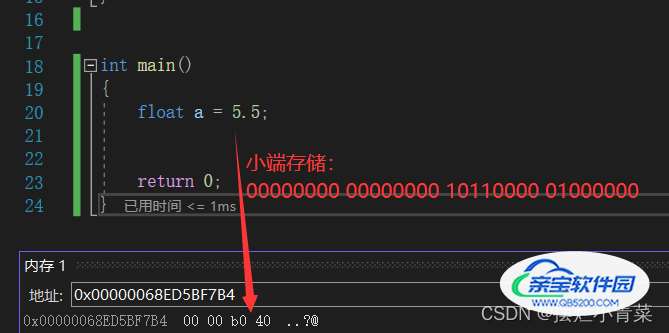
二.浮点数使用的第一个注意事项

由于浮点数存入时很可能发生有效数值M二进制序列的截断以及被截去的序列的最高位的四舍五入而造成精度损失，所以两个浮点数直接用操作符进行比较很可能会得到不符合预期的结果。

举个例子：

int main()
{
    float a = 3.12f;
    a += 0.02f;
   
    float b = 3.14f;
 
    std::cout << (a == b) << std::endl;
    std::cout << (a > b) << std::endl;
    std::cout << (a < b) << std::endl;
 
    return 0;
}

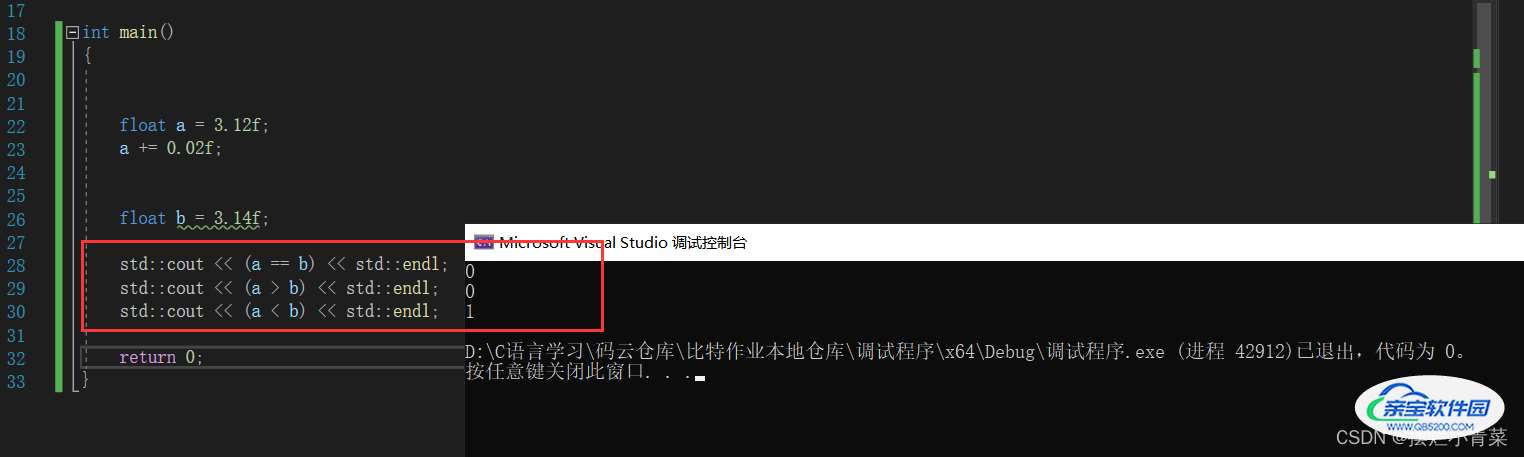
简单调试一下代码：

上述代码中，a最终的值和b的值在数学上应该是相同的，但是由于精度丢失而导致了最后a<b,如果这时a和b直接用运算符进行比较则无法得到预期的结果。

两个浮点数的比较应该使用如下方式：

对于浮点数而言比较合适的精度为：0.000001

对于双进度浮点数而言比较合适的精度为：0.0000000000000001

因此可以定义两个宏：

#define epf 1e-6
#define epd 1e-16

f,f1,f2代表单精度浮点数，d，d1,d2代表双精度浮点数。

判断浮点数是否等于0：

要判断一个单精度浮点数是否等于0：if(fabs(f) <= eps );
要判断一个双精度浮点数是否等于0：if(fabs(d) <= epd);
判断两个浮点数是否相等：

要判断两个单精度浮点数是否相等：if(fabs(f1 - f2) <= eps);
要判断两个双精度浮点数是否相等：if(fabs(d1 - d2) <= epd);

注：fabs是求浮点数绝对值的函数。声明在<iostream>头文件中。

#define eps 1e-6
int main()
{
    float a = 3.12f;
    a +=0.02f;
    float b = 3.14f;
    if (fabs(a - b) <= eps)
    {
        std::cout << "a==b" << std::endl;
    }
    else
    {
        std::cout << "a!=b" << std::endl;
    }
    return 0;
}

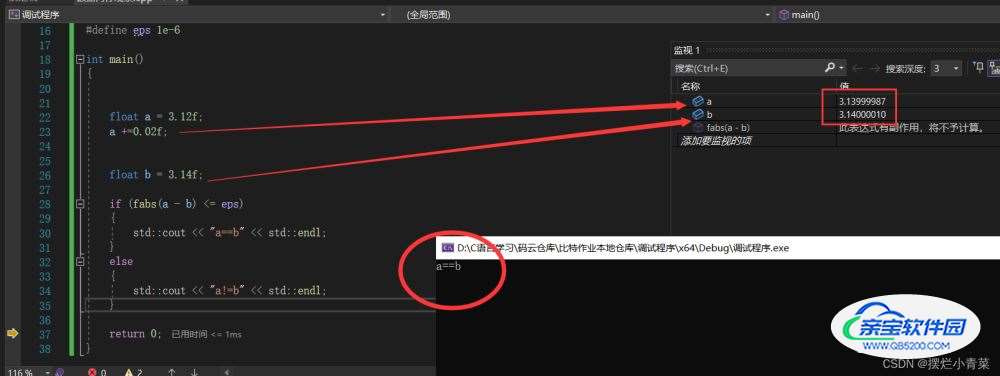
三.浮点数使用的第二个注意事项

由于浮点数存入时可能发生数据截断，因此两个绝对值相差巨大的浮点数进行加减运算很多时候是没有意义的。

以十进制数为例来说明这个问题：

代码验证：

int main()
{
    float a = 1e38;
    std::cout << a << std::endl;
    
    float b = 1000;
    a = a + b;
    std::cout << a << std::endl;
 
    a = a - b;
    std::cout << a << std::endl;
    return 0;
}

附：观察内存中的FLT_MAX和FLT_MIN

C/C++中的FLT_MAX都被宏定义为浮点数绝对值最大的值

将FLT_MAX存入内存中：

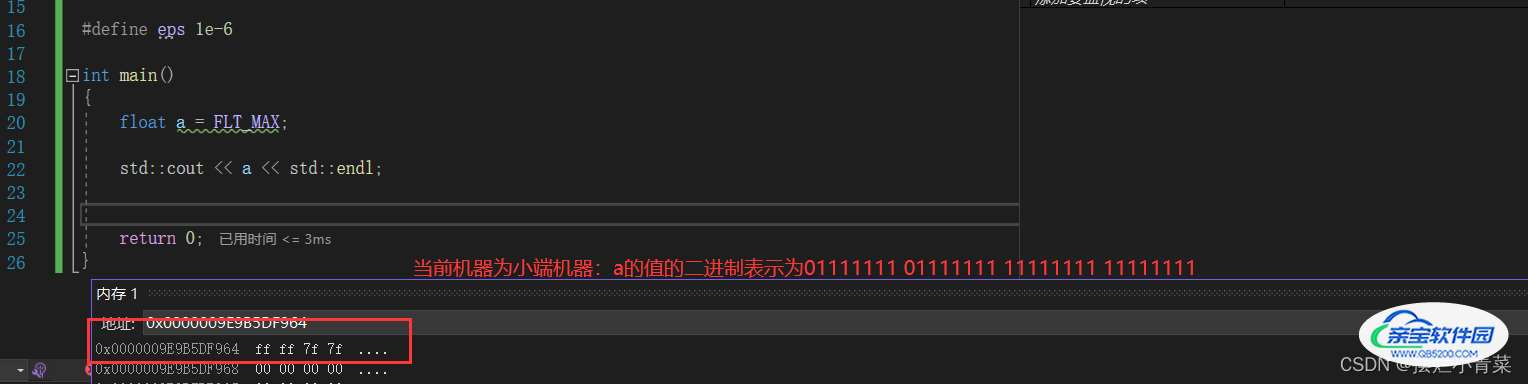
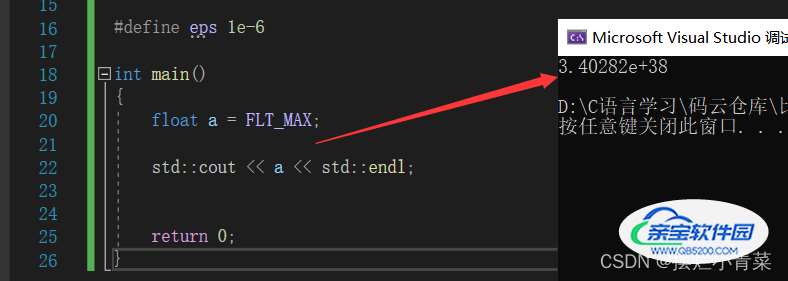
将a的二进制序列分割为SEM的形式：

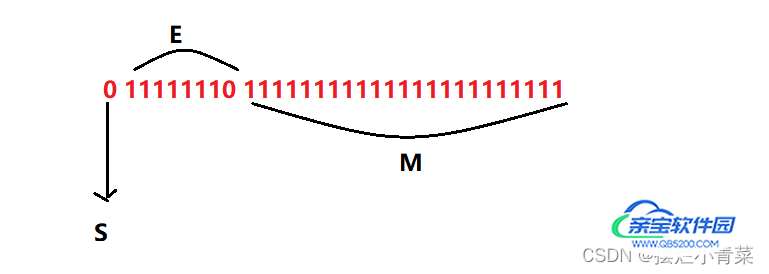
其指数位不是全1

C/C++中的FLT_MIN被宏定义为绝对值最接近于0的浮点数

将FLT_MIN存入内存中：

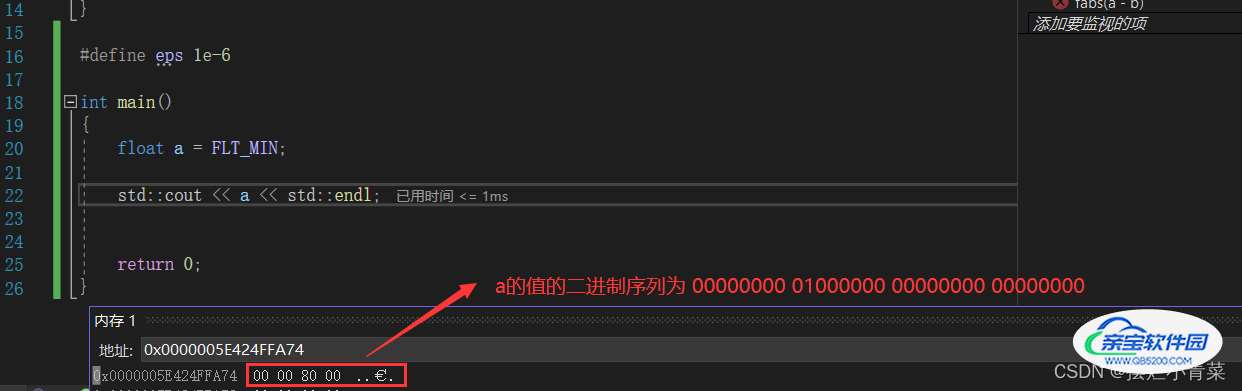
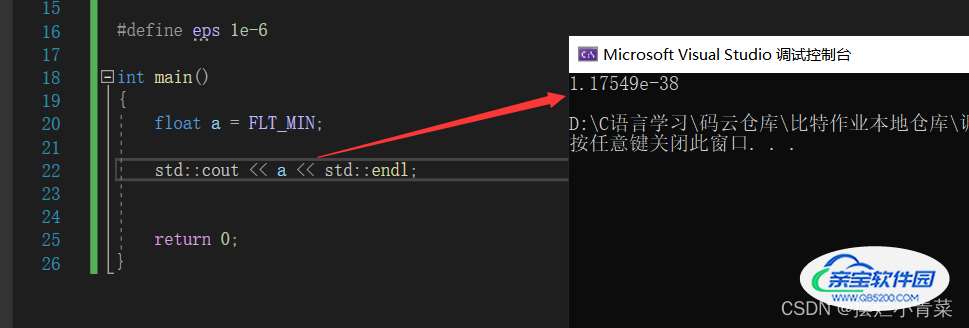
其指数位不是全0

补充：C 语言两个浮点数比较大小的办法

浮点数并非真正意义上的实数，只是其在某个范围内的近似。

因此两个浮点数比较大小时，不能简单地使用大于小于号进行比较，应该判断连个浮点数差值的绝对值是否近似为0。

#include <stdio.h>
#include <math.h>
 
// 这里的 EPS 是自己定义的精度
#define EPS 1e-7     // 判断浮点数是否位于0的一个很小的邻域内[-EPS,EPS]内

int main(void)
{
    /* 判断一个浮点数是否等于 0*/
    float a;
    scanf("%f", &a);
    if(fabs(a) <= EPS)  // a=0
        ...
    else if(a > EPS)    // a>0
        ...
    else                // a<0
        ...
 
    /* 比较两个浮点数大小 */
    float a,b;
    scanf("%f%f",&a, &b);
    if(fabs(a-b) <= EPS)  // a=b
        ...
    else if( (a-b) > EPS)  // a>b
        ...
    else                   // a<b
        ...
}

总结

加载全部内容