Three.js Interpolant实现动画插值
这个冰棍不太冷 人气:0Interpolant
这个类主要是用来实现插值,常用于动画。
可以把这个类理解为是一个数学函数,给定一个自变量,要返回对应的函数值。只是,在我们定义函数的时候,是通过一些离散的点进行定义的。
举个例子,加入我们要定义y = x^2这条曲线,我们需要定义两个数组(即采样点和采样的值):x = [-2, -1, 0, 1, 2],y = [4, 1 ,0, 1, 4]。通过这样的定义方式,我们怎么求不是采样点中的函数值?例如上面的吱吱,我们怎么求x = 0.5时的值?这就时我们要说的“插值”。
最常见也最简单的插值方式就是线性插值,还拿上面的例子讲,就是在“连点”画图象的时候,用直线把各点连起来。
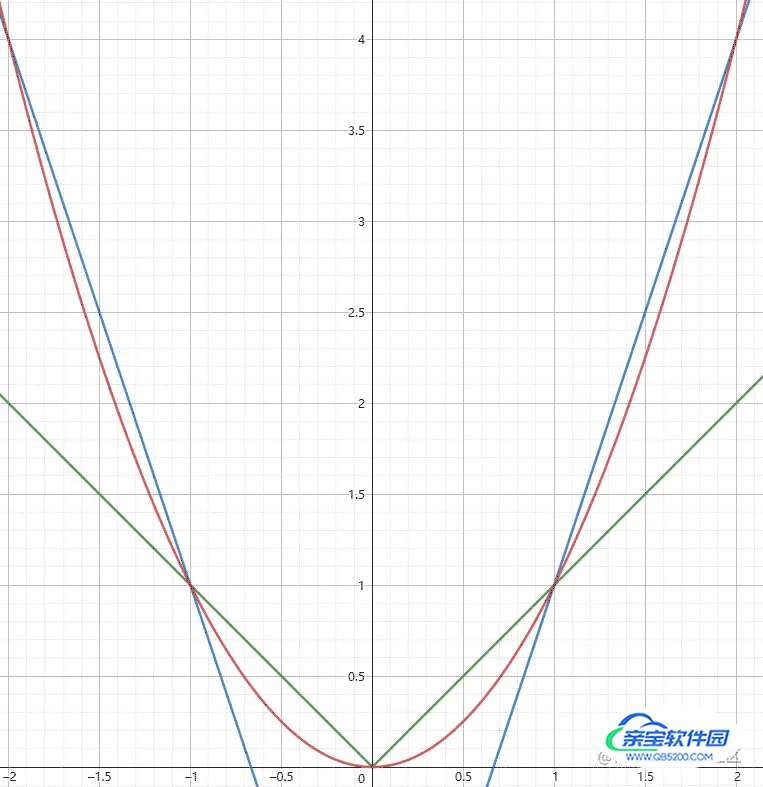
我们现在要取x=0.5,通过(0,0)和(1,1)线性插值,即求出过这两点的直线y=x,可以得到,y=0.5;同理,x=1.5时,通过(1,1)和(2,4)的直线为y=3x−2,可以得到,y=2.5。
我们使用three.js提供的线性插值验证一下:
import * as THREE from 'three' const x = [-2, -1, 0, 1, 2] const y = [4, 1, 0, 1, 4] const resultBuffer = new Float32Array(1) const interpolant = new THREE.LinearInterpolant(x, y, 1, resultBuffer) interpolant.evaluate(0.5) // 0.5 console.log(resultBuffer[0]) interpolant.evaluate(1.5) // 2.5 console.log(resultBuffer[0])
看不懂这段代码没有关系,接下来会慢慢解释。
通过离散的采样点定义曲线
在Interpolant的构造器,需要以下这些参数:
parameterPositions:采样的位置,类比成函数就是自变量的取值
sampleValues:采样取的值,类比成函数就是自变量对应的函数值
sampleSize:每个采样点的值,分量的个数。例:sampleValues可以表示一个三维空间的坐标,有x, y, z三个分量,所以sampleSize就是三。
resultBuffer:用来获取插值的结果,长度为sampleSize时,刚好够用。
这几个参数一般有着如下的数量关系:
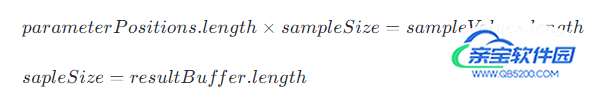
通过上面这些参数,我们就可以大概表示一个函数的曲线,相当于在使用“描点法”画图象时,把一些离散地采样点标注在坐标系中。
有了这些离散的点,我们就可以通过插值,求出任意点的函数值。
插值的步骤
1. 寻找要插值的位置
还拿上面的例子来说,parameterPositions = [-2, -1, 0, 1, 2],现在想要知道position = 1.5处的函数值,我们就需要在parameterPositions这个数组中找到position应该介于那两个元素之间。很显然,在这个例子中,值在元素1,2之间,下标在3,4之间。
2. 根据找到的左右两个点,进行插值
上面的例子中,我们找到的两个点分别是(1,1)和(2,,4)。可以有多种插值的方式,这取决于你的需求,我们仍然拿线性插值举例,通过(1,1)和(2,4)可以确定一条直线,然后把1.5带入即可。
Interpolant源码
Interpolant采用了一种设计模式:模板方法模式。
在插值的整个流程中,对于不同的插值方法来说,寻找插值位置这一操作是一样的,所以把这一个操作可以放在基类中实现。
对于不同的插值类型,都派生自Interpolant,然后实现具体的插值方法,这个方法的参数就是上面寻找到的位置。
1. 构造器
constructor(parameterPositions, sampleValues, sampleSize, resultBuffer) {
this.parameterPositions = parameterPositions;
this._cachedIndex = 0;
this.resultBuffer = resultBuffer !== undefined ?
resultBuffer : new sampleValues.constructor(sampleSize);
this.sampleValues = sampleValues;
this.valueSize = sampleSize;
this.settings = null;
this.DefaultSettings_ = {};
}
基本上就是把参数中的变量进行赋值,对于resultBuffer来说,如果不在参数中传递,那么就会在构造器中进行创建。
_cachedIndex放到后面解释。
2. copySampleValue_()
如果,我们要插值的点,刚好是采样点,就没必要进行计算了,直接把采样点的结果放到resultBuffer中即可,这个方法就是在做这件事,参数就是采样点的下标。
copySampleValue_(index) {
// copies a sample value to the result buffer
const result = this.resultBuffer,
values = this.sampleValues,
stride = this.valueSize,
offset = index * stride;
for (let i = 0; i !== stride; ++i) {
result[i] = values[offset + i];
}
return result;
}
3. interpolate_( /* i1, t0, t, t1 */ )
interpolate_( /* i1, t0, t, t1 */ ) {
throw new Error( 'call to abstract method' );
// implementations shall return this.resultBuffer
}
这个就是具体的插值方法,但是在基类中并没有给出实现。
4. evaluate()
接下来就是多外暴露的接口,通过这个方法计算插值的结果。
这段代码用了一个不常用的语法,类似C语言中的goto语句,可以给代码块命名,然后通过break 代码块名跳出代码块。
这段代码就是实现了上面说的插值的过程:
寻找位置
插值(调用interpolate_()方法)
整个validate_interval代码块,其实就是在找插值的位置。它的流程是:
- 线性查找
- 根据上一次插值的位置,向数组尾部的方向查找两个位置。(这里就是构造器中
_cachedIndex的作用,记录上一次插值的位置)。如果到了数组最后仍然没找到,则到数组头部去找;如果没有到数组尾部,则直接跳出线性查找,使用二分查找。
- 二分查找
为什么要先在上一次插值的左右位置进行线性查找呢?插值最常见的使用场景就是动画,每次会把一个时间传进来进行插值,而两次插值的间隔通常很短,分布在上一次插值的附近,可能是想通过线性查找优化性能。
evaluate(t) {
const pp = this.parameterPositions;
let i1 = this._cachedIndex,
t1 = pp[i1],
t0 = pp[i1 - 1];
validate_interval: {
seek: {
let right;
// 先进性线性查找
linear_scan: {
//- See http://jsperf.com/comparison-to-undefined/3
//- slower code:
//-
//- if ( t >= t1 || t1 === undefined ) {
forward_scan: if (!(t < t1)) {
// 只向后查找两次
for (let giveUpAt = i1 + 2; ;) {
// t1 === undefined,说明已经到了数组的末尾
if (t1 === undefined) {
// t0是最后一个位置
// 如果t < t0
// 则说明向数组末尾找,没有找到
// 因此跳出这次寻找 接着用其他方法找
if (t < t0) break forward_scan;
// after end
// t >= t0
// 查找的结果就是最后一个点 不需要进行插值
i1 = pp.length;
this._cachedIndex = i1;
return this.copySampleValue_(i1 - 1);
}
// 控制向尾部查找的次数 仅查找两次
if (i1 === giveUpAt) break; // this loop
// 迭代自增
t0 = t1;
t1 = pp[++i1];
// t >= t0 && t < t1
// 找到了,t介于t0和t1之间
// 跳出寻找的代码块
if (t < t1) {
// we have arrived at the sought interval
break seek;
}
}
// prepare binary search on the right side of the index
right = pp.length;
break linear_scan;
}
//- slower code:
//- if ( t < t0 || t0 === undefined ) {
if (!(t >= t0)) {
// looping?
// 上一次查找到数组末尾了
// 查找数组前两个元素
const t1global = pp[1];
if (t < t1global) {
i1 = 2; // + 1, using the scan for the details
t0 = t1global;
}
// linear reverse scan
// 如果上一次查找到数组末尾
// i1就被设置成了2,查找数组前2个元素
for (let giveUpAt = i1 - 2; ;) {
// 找到头了
// 插值的结果就是第一个采样点的结果
if (t0 === undefined) {
// before start
this._cachedIndex = 0;
return this.copySampleValue_(0);
}
if (i1 === giveUpAt) break; // this loop
t1 = t0;
t0 = pp[--i1 - 1];
if (t >= t0) {
// we have arrived at the sought interval
break seek;
}
}
// prepare binary search on the left side of the index
right = i1;
i1 = 0;
break linear_scan;
}
// the interval is valid
break validate_interval;
} // linear scan
// binary search
while (i1 < right) {
const mid = (i1 + right) >>> 1;
if (t < pp[mid]) {
right = mid;
} else {
i1 = mid + 1;
}
}
t1 = pp[i1];
t0 = pp[i1 - 1];
// check boundary cases, again
if (t0 === undefined) {
this._cachedIndex = 0;
return this.copySampleValue_(0);
}
if (t1 === undefined) {
i1 = pp.length;
this._cachedIndex = i1;
return this.copySampleValue_(i1 - 1);
}
} // seek
this._cachedIndex = i1;
this.intervalChanged_(i1, t0, t1);
} // validate_interval
// 调用插值方法
return this.interpolate_(i1, t0, t, t1);
}
上面的代码看着非常多,其实大量的代码都是在找位置。找到位置之后,调用子类实现的抽象方法。
5. LinearInterpolant实现interpolate_( /* i1, t0, t, t1 */ )方法
class LinearInterpolant extends Interpolant {
constructor(parameterPositions, sampleValues, sampleSize, resultBuffer) {
super(parameterPositions, sampleValues, sampleSize, resultBuffer);
}
interpolate_(i1, t0, t, t1) {
const result = this.resultBuffer,
values = this.sampleValues,
stride = this.valueSize,
offset1 = i1 * stride,
offset0 = offset1 - stride,
weight1 = (t - t0) / (t1 - t0),
weight0 = 1 - weight1;
for (let i = 0; i !== stride; ++i) {
result[i] =
values[offset0 + i] * weight0 +
values[offset1 + i] * weight1;
}
return result;
}
}

总结
Three.js提供了内置的插值类Interpolant,采用了模板方法的设计模式。对于不同的插值方式,继承基类Interpolant,然后实现抽象方法interpolate_。
计算插值的步骤就是先找到插值的位置,然后把插值位置两边的采样点传递给interpolate_()方法,不同的插值方式会override该方法,以产生不同的结果。
推导了线性插值的公式。
加载全部内容