C++数组模拟之单链表与双链表和栈和队列的实现过程

时间:2023-03-20 Ggggggtm 人气:0

前引

我们在数据结构中都学到过单链表、双链表、栈和队列，当我们实现的时候时使用结构体指针实现的。定义一个结构体，结构体中存储指针变量和存放数值的变量。当然，C++的STL库中已经有实现好的栈和队列，我们可以直接用。但是在做算法题时，有时候我们会发现超出时间限制。原因是我们用STL库中的栈和队列容器时，效率相对来说较慢。我们这时就引出用数组模拟实现栈和队列。用数组模拟实现的使用起来效率更高、更方便。当然，我们也会讲到用数组模拟实现单链表和双链表。

一、数组模拟实现单链表

1.1 数组模拟的单链表解析

用结构体实现单链表时，我们会在结构体中定义一个存放数据的变量和一个存放下一个数据地址的指针。那我们用数组模拟实现怎么找到下一个数据的呢？用数组实现单链表，我们定义两个数组即可。一个数组存放数据，另一个数组存放下一数据的下标（充当结构体中的指针）。我们之直节看代码，理解更加容易。

//e[i] 表示点i的值
//ne[i] 表示节点i的下一个数据的下标
//head 表示栈头下标
//idx 当前已经存储到第几个数据了
int head,e[N],ne[N],idx;
//初始化
void Init()
{
    head=-1;
    idx=0;
}
//头插
void InsertHead(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}
//在地k个节点后插入一个元素
 
void Insert(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}
//删除第k个节点
void remove(int k)
{
    ne[k]=ne[ne[k]];
}

我们再结合着一个例题看一下。

1.2 数组模拟实现单链表例题

实现一个单链表，链表初始为空，支持三种操作：

向链表头插入一个数；
删除第kk个插入的数后面的数；
在第kk个插入的数后插入一个数。

现在要对该链表进行MM次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第kk个插入的数并不是指当前链表的第kk个数。例如操作过程中一共插入了nn个数，则按照插入的时间顺序，这nn个数依次为：第11个插入的数，第22个插入的数，…第nn个插入的数。

输入格式：

第一行包含整数MM，表示操作次数。

接下来MM行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数xx。

D k，表示删除第kk个插入的数后面的数（当kk为00时，表示删除头结点）。

I k x，表示在第kk个插入的数后面再插入一个数xx（此操作中kk均大于00）。

输出格式：

共一行，将整个链表从头到尾输出。

数据范围：

1≤M≤1000001≤M≤100000

所有操作保证合法。

输入样例：

10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6

输出样例：

6 4 6 5

我们看一下这道题的答案,代码如下:

#include<iostream>
using namespace std;
const int N=100010;
//e[i] 表示点i的值
//ne[i] 表示节点i的下一个数据的下标
//head 表示栈头下标
//idx 当前已经存储到第几个数据了
int head,e[N],ne[N],idx;
//初始化
void Init()
{
    head=-1;
    idx=0;
}
//头插
void InsertHead(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}
//在地k个节点后插入一个元素
void Insert(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}
//删除第k个节点
void remove(int k)
{
    ne[k]=ne[ne[k]];
}
int main()
{
    int m;
    cin>>m;
    Init();
    while(m--)
    {
        char op;
        cin>>op;
        if(op=='H')
        {
            int x;
            cin>>x;
            InsertHead(x);
        }
        else if(op=='D')
        {
            int k;
            cin>>k;
            if(!k)
                head=ne[head];
            else
                remove(k-1);
        }
        else
        {
            int k,x;
            cin>>k>>x;
            Insert(k-1,x);
        }
    }
    for(int i=head;i!=-1;i=ne[i])
    {
        printf("%d ",e[i]);
    }
}

二、数组模拟实现双链表

2.1 数组模拟实现双链表解析

数组模拟实现双链表与数组模拟实现单链表大同小异。数组模拟实现双链表时我们需要定义三个数组，一个数组存放数据，一个数组存放该数据左边数据的下标（左指针），一个数组存放该数据右边数据的下标（右指针）。我们直接看代码：

//e[i] 是表示点i的值
//l[i] 表示节点i的左边指针是多少
//r[i] 表示节点i的右边指针是多少
//idx 存储当前已经用到那个点了
int e[N],l[N],r[N],idx;
//初始化
void Init()
{
    r[0]=1;
    l[1]=0;
    idx=2;
}
//在下标为k的右边插入一个元素
void Insert(int k,int x)
{
    e[idx]=x;
    r[idx]=r[k];
    l[idx]=k;
    l[r[k]]=idx;
    r[k]=idx;
    idx++;
}
//删除下标为k的元素
void remove(int k)
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}

我们发现，上面代码并没有定义在下标为k的左边插入一个数据，我们只定义了在下标为k的右边插入一个数据。为什么呢？因为可以用在下标为k的右边插入一个数据函数实现在下标为k的左边插入一个数据。我们只需要在下标为k的左边的数据的右边插入一个数据就相当于实现了在下标为k的左边插入一个数据。如下图，我们想在下标为3的左边插入一个数据，其实就是在下标为2的右边插入一个数据。

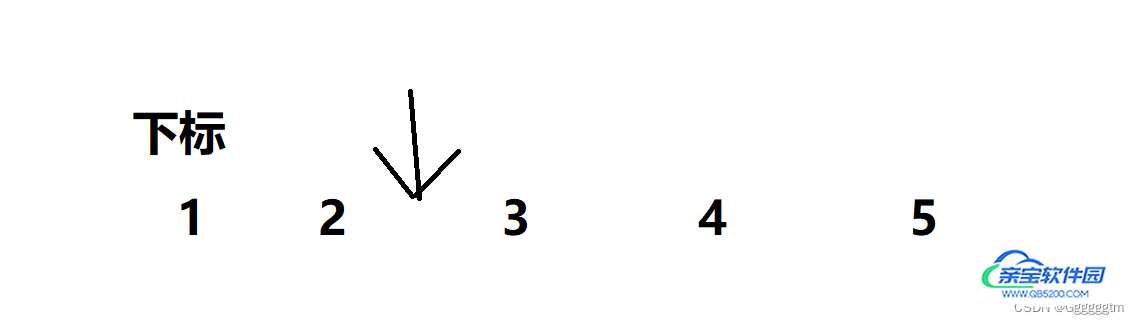
我们结合着一个例题理解一下。

2.2 数组模拟实现双链表例题

实现一个双链表，双链表初始为空，支持55种操作：

在最左侧插入一个数；
在最右侧插入一个数；
将第kk个插入的数删除；
在第kk个插入的数左侧插入一个数；
在第kk个插入的数右侧插入一个数

现在要对该链表进行MM次操作，进行完所有操作后，从左到右输出整个链表。

输入格式：

第一行包含整数MM，表示操作次数。

接下来MM行，每行包含一个操作命令，操作命令可能为以下几种：

L x，表示在链表的最左端插入数xx。
R x，表示在链表的最右端插入数xx。
D k，表示将第kk个插入的数删除。
IL k x，表示在第kk个插入的数左侧插入一个数。
IR k x，表示在第kk个插入的数右侧插入一个数。

输出格式：

共一行，将整个链表从左到右输出。

数据范围：

1≤M≤1000001≤M≤100000

所有操作保证合法。

输入样例：

10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2

输出样例：

8 7 7 3 2 9

我们看一下答案，代码如下：

#include<iostream>
using namespace std;
const int N=100010;
//e[i] 是表示点i的值
//l[i] 表示节点i的左边指针是多少
//r[i] 表示节点i的右边指针是多少
//idx 存储当前已经用到那个点了
int e[N],l[N],r[N],idx;
//初始化
void Init()
{
    r[0]=1;
    l[1]=0;
    idx=2;
}
//在下标为k的右边插入一个元素
void Insert(int k,int x)
{
    e[idx]=x;
    r[idx]=r[k];
    l[idx]=k;
    l[r[k]]=idx;
    r[k]=idx;
    idx++;
}
//删除下标为k的元素
void remove(int k)
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}
int main()
{
    int m;
    cin>>m;
    Init();
    while(m--)
    {
        string op;
        int x,k;
        cin>>op;
        if(op=="L")
        {
            cin>>x;
            Insert(0,x);
        }
        else if(op=="R")
        {
            cin>>x;
            Insert(l[1],x);
        }
        else if(op=="D")
        {
            cin>>k;
            remove(k+1);
        }
        else if(op=="IL")
        {
            cin>>k>>x;
            Insert(l[k+1],x);
        }
        else
        {
            cin>>k>>x;
            Insert(k+1,x);
        }
    }
    for (int i = r[0]; i != 1; i = r[i]) 
        cout << e[i] << ' ';
    return 0;
}

三、数组模拟实现栈

3.1 数组模拟实现栈解析

我们用数组模拟实现栈是相对简单的。我们只要满足栈的先进后出的性质即可。我们直接看代码，如下：

//********************* 模拟栈
int stack[N],top=0;
//往栈中插入元素
stack[top++];
//拿出栈顶元素
top--;
//栈顶元素
stack[top-1];
//判断栈是否为空
if(top>0)
{
    printf("notempty\n");
}
else
{
    printf("empty\n");
}

我们这里给出一个用到单调栈的例题。

3.2 数组模拟实现栈例题

给定一个长度为NN的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出−1−1。

输入格式：

第一行包含整数NN，表示数列长度。

第二行包含NN个整数，表示整数数列。

输出格式：

共一行，包含NN个整数，其中第ii个数表示第ii个数的左边第一个比它小的数，如果不存在则输出−1−1。

数据范围：

1≤N≤1051≤N≤105

1≤数列中元素≤1091≤数列中元素≤109

输入样例：

5
3 4 2 7 5

输出样例：

-1 3 -1 2 2

我们看一下答案，代码如下：

#include<iostream>
using namespace std;
const int N=100010;
int stack[N],top=0;
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int x=0;
        scanf("%d",&x);
        while(top&&stack[top-1]>=x)
        {
            top--;
        }
        if(!top)
            printf("-1 ");
        else
        {
            printf("%d ",stack[top-1]);
        }
        stack[top++]=x;
    }
    return 0;
}

四、数组模拟实现队列

4.1 数组模拟实现队列解析

同样，我们用数组模拟实现队列也是很简单的。我们只要满足队列的先进先出的性质即可。我们直接看代码，如下：

//********************* 模拟对列
int queue[N],head,tail=0;
//插入
queue[tail++]=x;
//弹出
head++;
//判断队列是否为空
if(head<tail) not empty;
else empty;
//取出对头，队尾元素
queue[head];
queue[tail-1];

我们这里给出一道用到队列的例题，相对来说难一点，我们看一下。

4.2 数组模拟实现队列例题

给定一个大小为n≤106n≤106的数组。

有一个大小为kk的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到kk个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为[1 3 -1 -3 5 3 6 7]，kk为33。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式：

输入包含两行。

第一行包含两个整数nn和kk，分别代表数组长度和滑动窗口的长度。

第二行有nn个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式：

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

我们看一下答案，代码如下：

#include<iostream>
using namespace std;
 
const int N=1000010;
int a[N],q[N];
int head,tail;
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    head=0;
    tail=0;
    for(int i=0;i<n;i++)
    {
        //判断对头是否已经划出窗口
        if(head<tail&&i-k+1>q[head])
            head++;
        //对头确定最小数
        while(head<tail&&a[q[tail-1]]>=a[i])
            tail--;
        q[tail++]=i;
        if(i>=k-1)
        printf("%d ",a[q[head]]);
    }
    printf("\n");
    head=0;
    tail=0;
    for(int i=0;i<n;i++)
    {
        //判断对头是否已经划出窗口
        if(head<tail&&i-k+1>q[head])
            head++;
        //对头确定最大数
        while(head<tail&&a[q[tail-1]]<=a[i])
            tail--;
        q[tail++]=i;
        if(i>=k-1)
        printf("%d ",a[q[head]]);
    }
    return 0;
}

加载全部内容