C语言中关于树和二叉树的相关概念
[Pokemon]大猫猫 人气:0树是一种 非线性的 数据结构,由 n(n >= 0) 个 有限节点 组成一种 具有层次关系 的集合
一、树
树的结构可以递归定义为:
根节点除根节点之外,其余节点被分成 M(M >= 0) 个互不相交的集合,每个集合分别是一棵子数
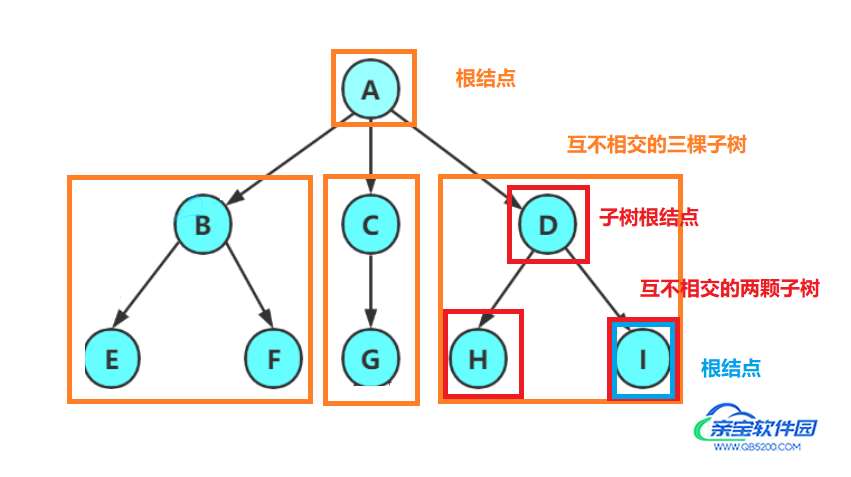
0 个结点的树就称为空树
- 树中除 根节点没有前驱节点 之外,其余每个节点都 有且仅有一个前驱节点,因此 n 个节点的树有 n - 1 条边
- 树中 每个节点 都可以 有 0 个或多个后继节点
树的相关概念
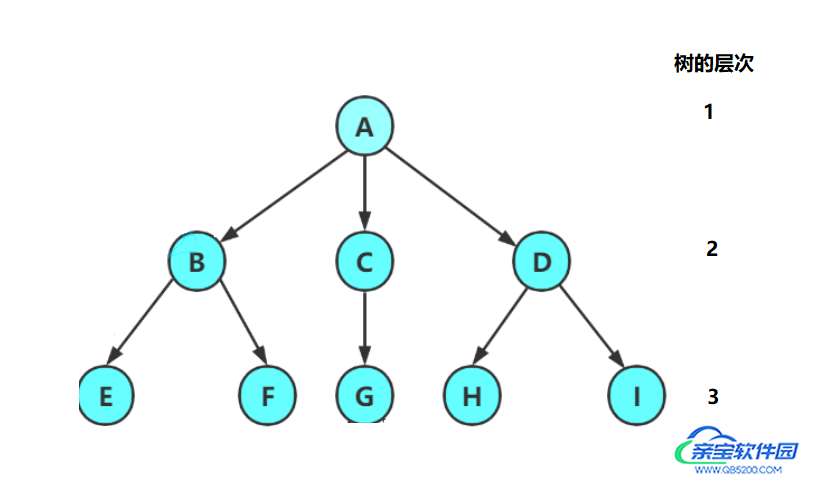
- 节点的度:节点含有的 子树个数,如图中 A 节点的度为 3
- 叶节点或终端节点:节点的 度为 0,如图中 E、F、G、H、I
- 分支节点或非终端节点:节点的 度不为 0,如图中 A、B、C、D
- 父节点或双亲节点:若一个节点含有子节点,则这个节点称为其子节点的父节点,如图中 B 是 E 和 F 的父节点
- 子节点或孩子节点:若一个节点含有子树,子树的根节点 称为该节点的子节点,如图中 E 和 F 都是 B 的子节点
- 兄弟节点:父节点相同 的节点互为兄弟节点,如图中 E 和 F 互为兄弟节点
- 树的度:树中所有节点的度中的最大值,如图中 A 节点的度为 3,是树中所有节点的度中的最大值,即树的度为 3
- 节点的层次:如上图,从根节点开始定义为第一层,根节点的子节点为第二层 …,(将根节点层次定义为 0 也是可以的)
- 树的高度或深度:树中节点的最大层次,图中为树的高度为 3
- 堂兄弟节点:父节点在同一层次的结点,如图中 E、F、G、H、I 结点互为堂兄弟节点
- 节点的祖先:根节点到该节点路径上的所有节点, A、B 结点是 E 的祖先
- 子孙:以某节点为根的子树中任一节点 都称为该节点的子孙,如上图:所有节点都是 A 的子孙
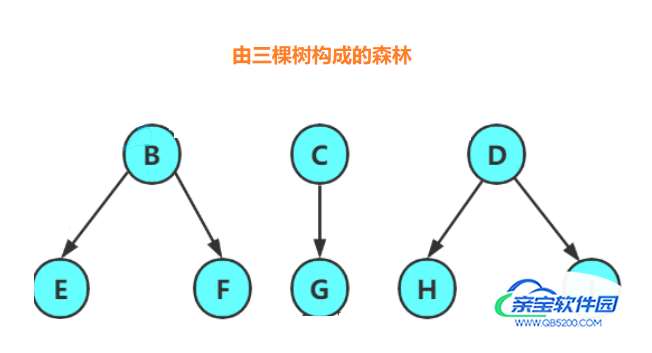
森林:由 M(M > 0) 棵 互不相交的树 构成的集合,将上图中 A 节点去掉后,便构成由以 B、C、D 为根节点的三颗树构成的森林
树的存储结构
在树的结构中可以发现,树是不易于用数组来存储的,因此 采用链式的方式来存储树
结构1:
由于树的结构中 每个节点的孩子个数是不确定的,因此每个节点需要使用一个顺序表存储孩子的指针
typedef int TreeDataType;
typedef struct TreeNode
{
TreeDataType data;
SeqList childs; //顺序表,并且每个元素的类型是 struct TreeNode*
}TreeNode;
结构2:
孩子兄弟表示法:节点的第一个孩子用该节点中的孩子指针指向,第二个孩子用该结点的第一个孩子结点的兄弟指针指向,第三个孩子用该节点的第二个孩子结点的兄弟指针指向…
typedef int TreeDataType;
typedef struct TreeNode
{
TreeDataType data;
struct TreeNode* child;
struct TreeNode* brother;
}TreeNode;
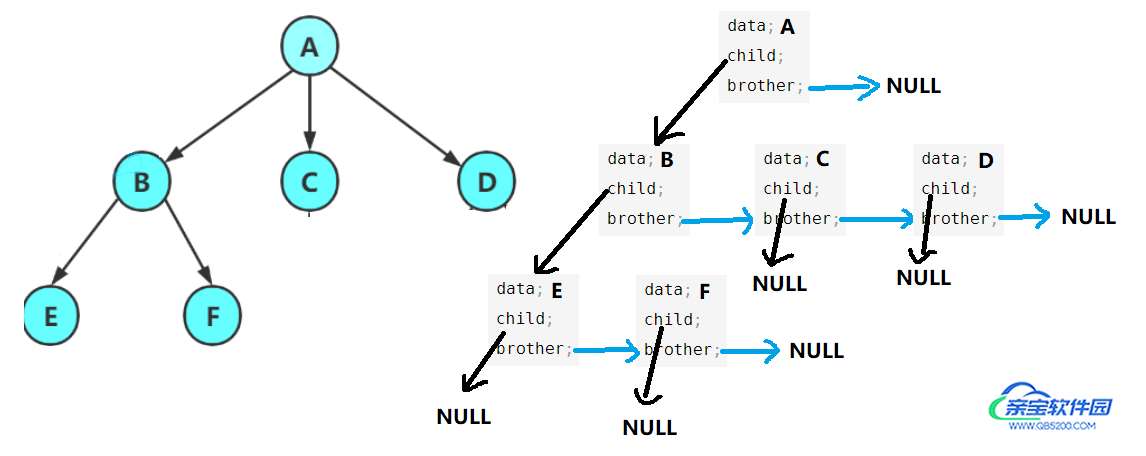
存储树的方法还有双亲表示法,孩子表示法、孩子双亲表示法等,感兴趣的读者可以自行查阅
二、二叉树
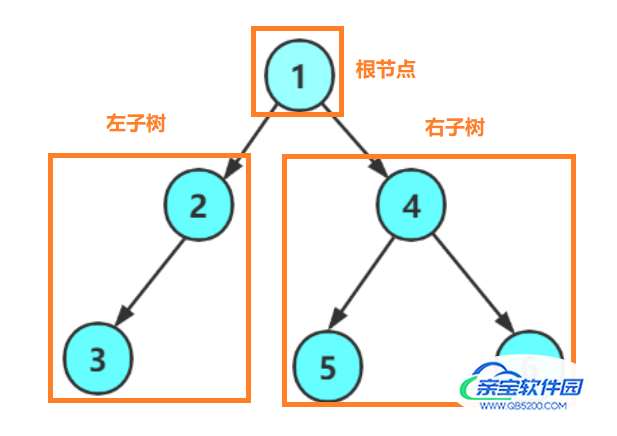
树中 所有结点的度都小于等于 2 的树,即树的度小于等于 2 的树,称为二叉树
在二叉数中子树有左右区分,次序不能颠倒,左边的称为左子树,右边的称为右子树
二叉树的递归定义为:
- 根节点
- 左子树和右子树
左子树和右子树可以为空树,这里的子树也是一颗二叉树
二叉树的性质
假定根节点的层数为 1
- 一棵非空二叉树的第 i 层上最多有 2^(i - 1)个节点
- 深度为 h 的二叉树的最大节点数是 2^h - 1
- 任何一棵二叉树,如果度为 0 的叶节点个数为 n0,度为 2 的分支节点个数为 n2,则有 n0 = n2 +1,即度为 0 的节点,比度为 2 的节点多 1
假设一颗二叉树有 n 个节点,度为 0 的节点数为 n0,度为 1 的节点数为 n1,度为 2 的节点数为 n2,根据 n 个节点的二叉树有 n - 1 条边,可得到如下关系:
- n0 * 0 + n1 * 1 + n2 * 2 = n - 1
- n0 + n1 + n2 = n
解得:n0 = n2 + 1
满二叉树:如果二叉树中每一个层的节点数都达到最大值,则这棵二叉树称为满二叉树
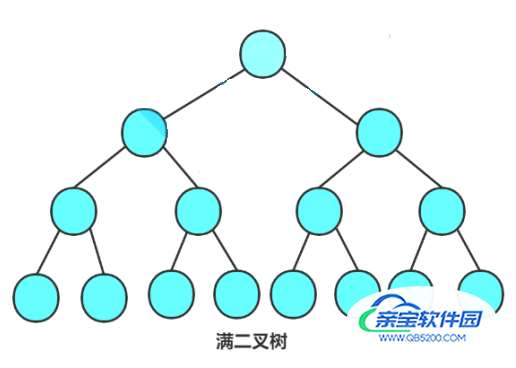
假设一棵二叉树的层数为 K,且节点总数是 2^K - 1,则它就是满二叉树
完全二叉树:假设一颗二叉树有 K 层,如果这颗二叉数的前 K - 1 层是满二叉树,并且第 K 层是从左往右还是连续的节点,则这棵二叉树称为完全二叉树
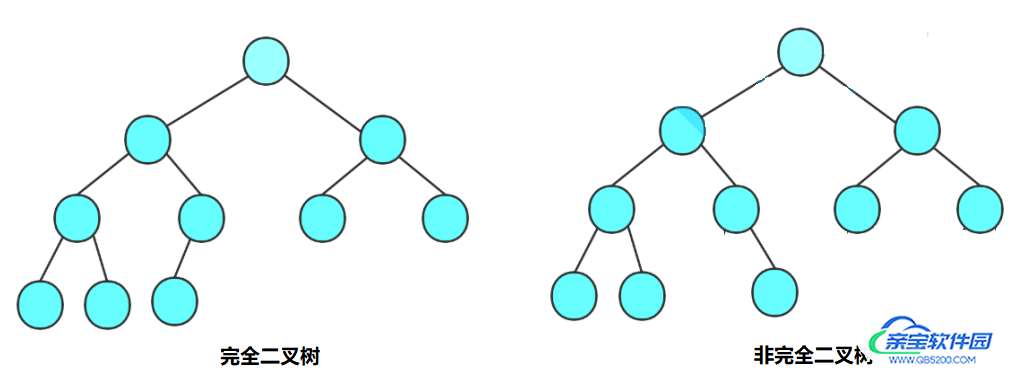
假设一棵完全二叉树的层数为 K ,则完全二叉树节点数的范围:2^(K - 1) ~ 2^K - 1
完全二叉树中度为 1 的节点有 0 个或 1 个
满二叉树可以认为是一种特殊的完全二叉树
- 具有 n 个节点的 满二叉树 的深度 h = log2(n + 1),n 个节点的 完全二叉树 的深度 h = log2(n + 1),h 向上取整(2.1 取 3)
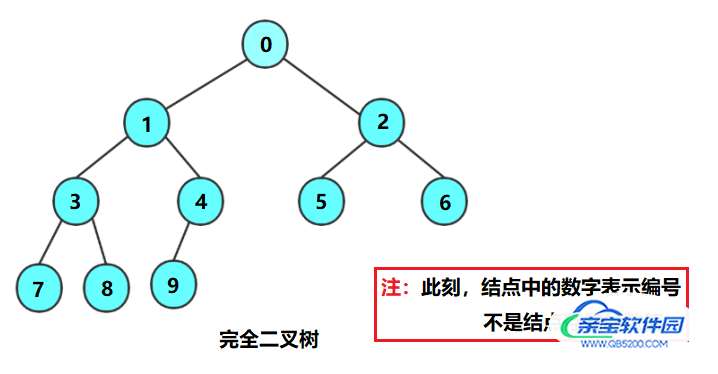
- 对于具有 n 个节点的 完全二叉树,按照 从上至下、从左至右 的顺序,对所有节点从 0 开始依次编号
由于完全二叉树中从第二层开始,每一层的结点都是偶数个,因此 左孩子的编号都均为奇数,右孩子的编号都均为偶数
在 n 个节点的 完全二叉树 中,对于合法的编号为 i 的节点有:
- i 节点的 左孩子 的编号为 2 * i + 1,如果 2 * i + 1 < n,表示没有左孩子
- i 节点的 右孩子 的编号为 2 * i + 2,如果 2 * i + 2 < n,表示没有右孩子
- 根据 1 和 2 可知 i 节点的 父节点 的编号为 (i - 1) / 2,如果 i = 0,表示为根节点,没有父节点
加载全部内容