numpy之sum()的使用及说明

numpy之sum()

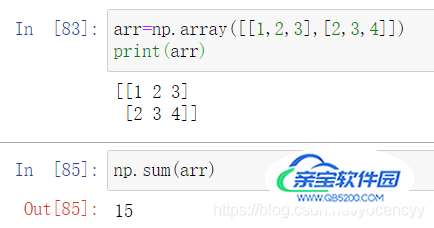
sum(a)默认为对输入参数中的所有元素进行求和

>>> a
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
>>> np.sum(a)
66


>>> b=np.arange(12)
>>> b=b.reshape(2,6)
>>> b
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11]])
>>> np.sum(b)
66

sum()输入参数带有axis时，将按照指定axis进行对应求和

>>> b=np.arange(12)
>>> b=b.reshape(2,6)
>>> b
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11]])
>>> np.sum(b)    #默认对所有元素进行求和
66
>>> np.sum(b,axis=0)        #在第一个轴展开方向上求和
array([ 6,  8, 10, 12, 14, 16])
>>> np.sum(b,axis=1)
array([15, 51])
>>> 

sum()输入参数axis为多个轴时，则依次按要求在axis上进行多次求和

>>> a=np.arange(12).reshape(2,2,3)
>>> a
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])

>>> b=np.sum(a,axis=(0,1))    #分别在axis=0 和 1两个方向上进行求和
>>> b
array([18, 22, 26])
>>> b=np.sum(a,axis=(1,2))
>>> b
array([15, 51])

>>> b=np.sum(a,axis=(0,1,2))    #由于a为3为矩阵，所有在三个axis上分别求和相当于对所有元素进行求和 
>>> b
66

生动理解numpy.sum()以及其axis参数

1、numpy.sum()方法

使用NumPy模块时，经常会用到numpy.sum()方法，比如计算一个多维数组(ndarray)的所有元素之和：

sum()方法的计算原理是Sum of array elements over a given axis. 对指定维度axis上的元素进行求和，返回An array with the same shape as a（注：a是求和函数的输入数组）,  with the specified axis removed. 返回结果的shape和输入差不多，只是少了axis那一维度。

所以，如果输入数组a的维度是3，shape是 (2,3,5) ，numpy.sum(a, axis=0)返回的数组shape是 (3,5) ,numpy.sum(a, axis=1)返回的数组shape是(2,5)，numpy.sum(a, axis=2)返回的数组shape是 (2,3) 。

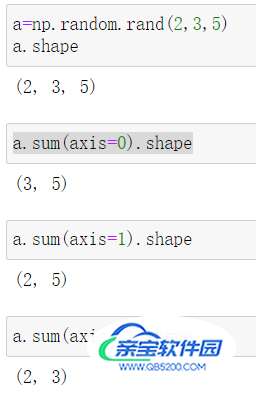
回到我刚才的问题，计算一个二维数组每一列的元素和，那么“列”到底对应哪一维度？axis=0还是axis=1？

arr是一个2行3列的数组，我要计算每一列的元素和，显然返回结果的shape应该是 (3,)，所以axis=0！

sum()中还有一个参数是keepdims，默认值是False。如果我们想让返回结果的维度数(ndim)和输入相同，把keepdimes设置为True就可以了，sum()返回结果就变成了：返回结果的shape和输入差不多，只是axis那一维度值为1。

2、numpy中axis的意义

NumPy用ndarray表示多维数组，多维数组，顾名思义，就是有多个维度的数组。比如向量(vector)只有一个维度，它是一维数组，矩阵(matrix)有两个维度，它是二维数组，三维以上的数组数学上称为张量(tensor)。

每个维度就对应一条坐标轴。比如平面直角坐标系，它是二维的，有两条坐标轴。

axis取值范围则对应ndarray对象的维度：一维数组时axis=0，二维数组时axis=0，1，维数越高，则axis可取的值越大，数组n维时，axis=0，1，…，n-1，维度序号0表示ndarray对象最外层[]的维度，序号越大对应ndarray对象越内层[]的维度。

• axis = 0表示按照最外层[]的维度的元素数目（shape）作分割，做块与块之间的运算，同时，若keepdims参数为False（默认），还要移除最外层[]；
• axis = 1表示对第二外层[]的维度的元素数目（shape）作分割，做块与块之间的运算，同时，若keepdims参数为False（默认），移除第二外层[]；
• axis = 2，3，4，5...也如此分析。

3、举个更具象的栗子

为了使抽象思考具象化，我根据生活中熟悉的小区房屋分布，模拟出一个开发商楼盘面积分布图，辅助思考：

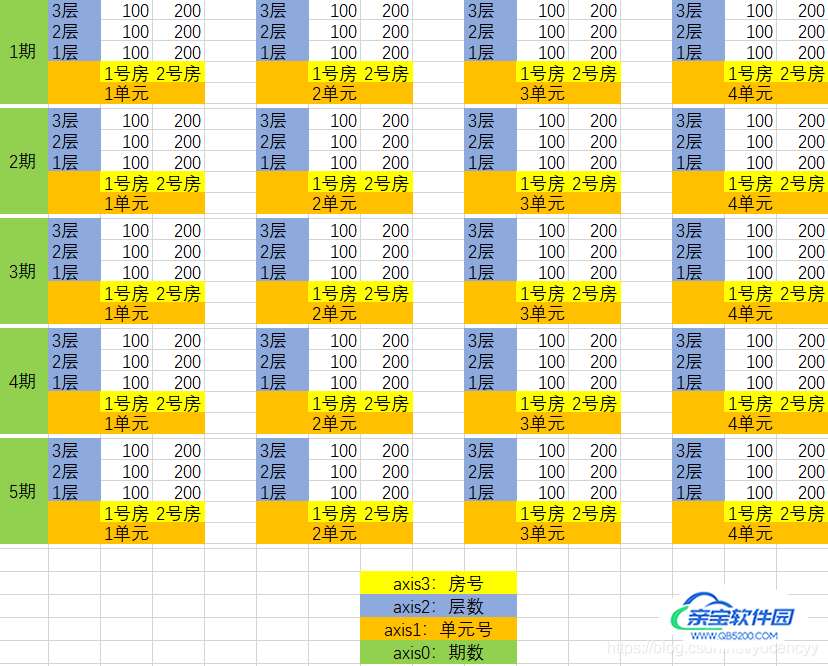
3.1、图中每个房子各有自己面积（单位：平方米），各个房子面积数据以标量形式存储在一个4维的，shape=(5,4,3,2)的numpy.array对象里；

3.2、axis3,2,1,0四个维度分别代表房号、层数、单元号、小区期数；

3.3、显而易见，依照小区的结构来看，这四个维度的地位并不相等，它们之间存在层级关系，其实这也正好和numpy.array对象的数据结构一致。所以，如果你喜欢，还可以假设一座城市有若干个这样的小区，然后一个省有若干个这样的城市，一个国家有若干个这样的省，一个星球有若干个这样的国家......什么，禁止套娃？哦对，numpy.array的维度就是在套娃嘛，它里面各自的维度可不像长宽高一样地位相同；

3.4、再来解读一下不同的axis参数下运算的意义（请注意白格子里的数字是怎样变化的）：

3.4.1 若以sum(axis=0)计算，则意味着按照单元数、层数、房号都一样（即axis3,axis2,axis1这3个维度的index都一样）的原则，把不同期数房子的面积汇总成为新的标量：

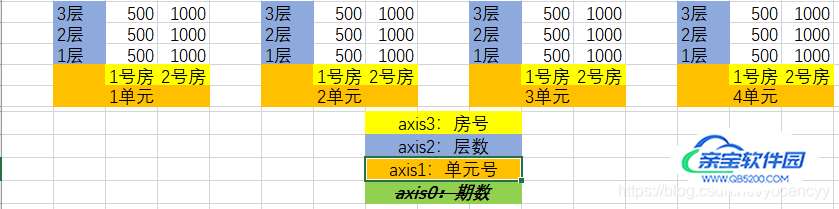
如上图，标量的意义也随之变化了。这些新的标量以shape=(4,3,2)的3个维度共同构成新的数组。因为汇总的是最顶层的维度axis0，所以生成的新数组只有1个。它替代了原先最顶层的数组，自己当了大佬，跳出了坑；

3.4.2 若以sum(axis=1)计算，则意味着按照层数、房号都一样（即axis3,axis2这2个维度的index都一样）的原则，在各自期数的小区里不同单元房子的面积汇总成为新的标量：

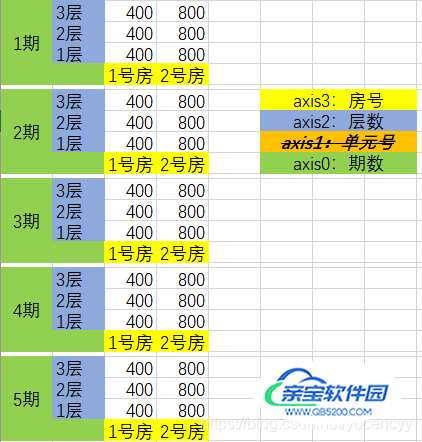
如上图，标量的意义也随之变化了。这些新的标量以shape=(3,2)的2个维度共同构成新的数组。因为汇总的维度是axis1，它上层还有size=5的维度axis0，所以生成的新数组有5个。它们分别砍掉了各自的shape=(4,3,2)的直系上司,自己做起了shape=(3,2)的中层领导。但可惜他们上层还有一个size=5的名叫axis0的大佬级维度没砍到，所以老实蹲在axis0的5个坑中；

3.4.3 若以sum(axis=2)计算，则意味着按照房号都一样（即axis3这1个维度的index都一样）的原则，在各单元里不同层数房子的面积汇总成为新的标量：

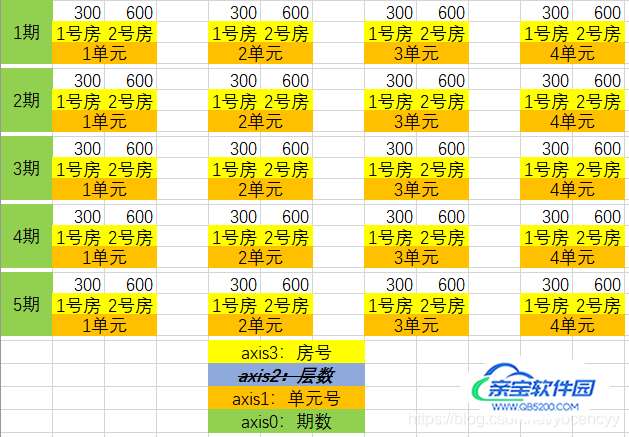
如上图，标量的意义也随之变化了。这些新的标量以shape=(2)的1个维度共同构成新的数组。

因为汇总的维度是axis2，它上层还有size=4的维度axis1和size=5的维度axis0，所以生成的新数组有5x4个，它们分别砍掉了各自的shape=(3,2)的直系上司,自己做起了shape=(2)小领导。但可惜他们上层有size=4的axis1维度，上上层有size=5的axis0维度没砍到，所以蹲在axis0和axis1构成的5x4个坑中；

3.4.4 若以sum(axis=3)计算，则意味着在各层数里不同房号房子的面积汇总成为新的标量：

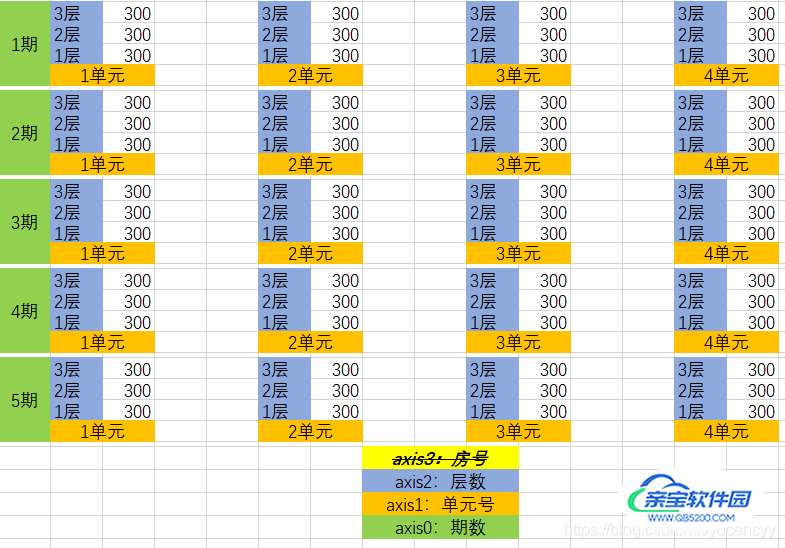
如上图，标量的意义也随之变化了。最底层的维度为1的数组axis3再降维汇总只能变成标量。

因为汇总的维度是axis3，它上层还有size=3的维度axis2、size=4的维度axis1和size=5的维度axis0，所以生成的新标量有5x4x3个，它们分别砍掉了各自的shape=(2)的直系上司，然鹅自己依旧没有下属，依然是个标量弟弟。且他们上层还有size=3的维度axis2，上上层还有size=4的维度axis1，上上上层还有size=5的维度axis0没砍到，所以蹲在axis0和axis1和axis2构成的5x4x3个坑中不能翻身。

4、总结

以上看出来什么规律了吗？首先，是层次化的结构，numpy.array对象里各个维度的地位并不相等，如果按地位相等的思考方式来考虑不同axis参数的运算，那我估计你脑袋就要炸了。numpy.array对象里各个维度之间存在层级关系，这是重要的思想方式，因为总-分的层级关系，才使得众多维度的变换符合人脑的思维方式，这与树形数据结构、分治算法等思想不谋而合。

其次，当参数axis选定一个值（假设为d）后，那么numpy.array.sum()方法只会对指定d维度上的k(假设k为维度d的元素个数)个元素（可以是标量、矩阵、或是张量）进行合并求和，更高的维度（即维度0,1,...,d-1）的结构不会发生变动。

至于元素与元素之间的运算，如果元素是标量，它们的求和你会吧？这是小学一年级的技能。如果矩阵求和呢？不会请翻本科线性代数教材。张量求和不会？别开玩笑了，如果你会矩阵求和，那也自然而然懂得张量求和。不会的话再回头看看上面的例子，或者自己找多几个例子。

除了sum函数，numpy中诸如argmin等包含axis参数的函数工作原理都相同。

最后

以上为个人经验，希望能给大家一个参考，也希望大家多多支持。