PyTorch 迁移学习实战

时间:2023-02-03 _23_ 人气:0

1. 实验环境

Jupyter Notebook
Python 3.7
PyTorch 1.4.0

2. 实验目的

迁移学习，让机器拥有能够“举一反三”的能力。
本次实验就以“是蚂蚁还是蜜蜂”为例，探索如何将已训练好的大网络迁移到小数据集上，并经过少量数据集的训练就让它获得非常出众的效果。

3. 相关原理

使用 PyTorch 的数据集套件从本地加载数据的方法
迁移训练好的大型神经网络模型到自己模型中的方法
迁移学习与普通深度学习方法的效果区别
两种迁移学习方法的区别

4. 实验步骤

# 下载实验所需数据并解压
!wget http://labfile.oss.aliyuncs.com/courses/1073/transfer-data.zip
!unzip transfer-data.zip

4.1 数据收集

实验中的数据是已经准备好的，训练数据集在 ./data/train 中，校验数据集在 ./data/val 中。（推荐直接到蓝桥云课上进行实验）。如果使用自己的环境只需要自己准备相关图片数据，并将代码中的路径改成你自己的数据集路径。

#引入实验所需要的包
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np
import torchvision
from torchvision import datasets, models, transforms
import matplotlib.pyplot as plt
import time
import copy
import os

4.1.1加载数据

使用 datasets 的 ImageFolder 方法就可以实现自动加载数据，因为数据集中的数据可能分别在不同的文件夹中，要让所有的数据一起加载。

# 数据存储总路径
data_dir = 'transfer-data'
# 图像的大小为224*224
image_size = 224
# 从data_dir/train加载文件
# 加载的过程将会对图像自动作如下的图像增强操作：
# 1. 随机从原始图像中切下来一块224*224大小的区域
# 2. 随机水平翻转图像
# 3. 将图像的色彩数值标准化
train_dataset = datasets.ImageFolder(os.path.join(data_dir, 'train'),
                                    transforms.Compose([
                                        transforms.RandomResizedCrop(image_size),
                                        transforms.RandomHorizontalFlip(),
                                        transforms.ToTensor(),
                                        transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
                                    ])
                                    )

# 加载校验数据集，对每个加载的数据进行如下处理：
# 1. 放大到256*256像素
# 2. 从中心区域切割下224*224大小的图像区域
# 3. 将图像的色彩数值标准化
val_dataset = datasets.ImageFolder(os.path.join(data_dir, 'val'),
                                    transforms.Compose([
                                        transforms.Resize(256),
                                        transforms.CenterCrop(image_size),
                                        transforms.ToTensor(),
                                        transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
                                    ])
                                    )

下面要为每个数据集创建数据加载器。

# 创建相应的数据加载器
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size = 4, shuffle = True, num_workers=4)
val_loader = torch.utils.data.DataLoader(val_dataset, batch_size = 4, shuffle = True, num_workers=4)

# 读取得出数据中的分类类别数
# 如果只有蜜蜂和蚂蚁，那么是2
num_classes = len(train_dataset.classes)
num_classes

输出：2

4.1.2 GPU运算

第一次了解GPU运算是在第一篇博客PyTorch，简单的了解了一下。

深度学习可以通过 GPU 并行运算加速模型的训练。
PyTorch 是支持使用 GPU 并行运算的。但是能不能使用 GPU 加速运算还取决于硬件，支持 GPU 的硬件（显卡）一般是比较昂贵的。
如果你想让自己的程序能够自动识别 GPU 计算环境，并且在 GPU 不具备的情况下也能自动使用 CPU 正常运行，可以这么做：
这三个变量，之后会用来灵活判断是否需要采用 GPU 运算。

# 检测本机器是否安装GPU，将检测结果记录在布尔变量use_cuda中
use_cuda = torch.cuda.is_available()

# 当可用GPU的时候，将新建立的张量自动加载到GPU中
dtype = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
itype = torch.cuda.LongTensor if use_cuda else torch.LongTensor

4.2 数据预处理

该函数作用：将数据集中的某张图片打印出来。

def imshow(inp, title=None):
    # 将一张图打印显示出来，inp为一个张量，title为显示在图像上的文字

    # 一般的张量格式为：channels * image_width * image_height
    # 而一般的图像为 image_width * image_height * channels 
    # 所以，需要将张量中的 channels 转换到最后一个维度
    inp = inp.numpy().transpose((1, 2, 0)) 

    #由于在读入图像的时候所有图像的色彩都标准化了，因此我们需要先调回去
    mean = np.array([0.485, 0.456, 0.406])
    std = np.array([0.229, 0.224, 0.225])
    inp = std * inp + mean
    inp = np.clip(inp, 0, 1) 

    #将图像绘制出来
    plt.imshow(inp)
    if title is not None:
        plt.title(title)
    plt.pause(0.001)  # 暂停一会是为了能够将图像显示出来。

将训练数据集的第一个 batch 绘制出来：

#获取第一个图像batch和标签
images, labels = next(iter(train_loader))

# 将这个batch中的图像制成表格绘制出来
out = torchvision.utils.make_grid(images)

imshow(out, title=[train_dataset.classes[x] for x in labels])

4.3 创建模型

该实验先训练一个普通的卷积神经网络，但正确率勉强达到50%上下。模型预测的效果很差。因为该实验选用的是蚂蚁和蜜蜂的图像数据，本身就很难识别，简单的卷积神经网络应付不了这种复杂的情况。其次，该实验的图片训练样本只有244个，数量级太小。

代码略

简单卷积神经网络取得的效果：（黄色曲线是测试数据集错误率，蓝色曲线是训练数据集错误率。）

因此，这里提到使用“加载已训练好的 ResNet 进行迁移学习”。
ResNet 是微软亚洲研究院何凯明团队开发的一种极深的特殊的卷积神经网络。该网络的原始版本曾号称是“史上最深的网络”，有 152 层，在物体分类等任务上具有较高的准确度。

考虑到原始的 ResNet 具有较大的复杂性，在本次实验中，实际迁移的是一个具有 18 层的精简版的 ResNet。该网络由 18 个串联在一起的卷积模块构成，其中每一个卷积模块都包括一层卷积一层池化。下面将加载 ResNet 模型，并观察模型的组成部分。如果是第一次运行，那么模型会被下载到 ~/.torch/models/ 文件夹中。

torch.utils.model_zoo.load_url('http://labfile.oss.aliyuncs.com/courses/1073/resnet18-5c106cde.pth')
# 加载模型库中的residual network，并设置pretrained为true，这样便可加载相应的权重
net = models.resnet18(pretrained=True)
#如果存在GPU，就将网络加载到GPU上
net = net.cuda() if use_cuda else net
# 将网络的架构打印出来
net

从模型的组成部分中，可以看到最后有一层全连接层，也就是 (fc): Linear(in_features=512, out_features=1000)。

4.3.1 构建迁移模型

下面把 ResNet18 中的卷积模块作为特征提取层迁移过来，用于提取局部特征。同时，将 ResNet18 中最后的全连接层（fc）替换，构建一个包含 512 个隐含节点的全连接层，后接两个结点的输出层，用于最后的分类输出。
整个模型的前面大部分的结构都是 ResNet，最后两层被替换成了自定义的全连接层。

# 读取最后线性层的输入单元数，这是前面各层卷积提取到的特征数量
num_ftrs = net.fc.in_features

# 重新定义一个全新的线性层，它的输出为2，原本是1000
net.fc = nn.Linear(num_ftrs, 2)

#如果存在GPU则将网络加载到GPU中
net.fc = net.fc.cuda() if use_cuda else net.fc

criterion = nn.CrossEntropyLoss() #Loss函数的定义
# 将网络的所有参数放入优化器中
optimizer = optim.SGD(net.parameters(), lr = 0.0001, momentum=0.9)

4.3.2 训练模型+测试+绘制图表

在训练阶段，迁移过来的 ResNet 模块的结构和所有超参数都可以保持不变，但是权重参数则有可能被新的数据重新训练。是否要更新这些旧模块的权重参数完全取决于我们采取的迁移学习方式。
迁移学习主要有两种模式：预训练模式和固定值模式。
接下来会分别介绍

4.3.2.1 预训练模式

record = [] #记录准确率等数值的容器

#开始训练循环
num_epochs = 20
net.train(True) # 给网络模型做标记，标志说模型在训练集上训练
best_model = net
best_r = 0.0
for epoch in range(num_epochs):
    #optimizer = exp_lr_scheduler(optimizer, epoch)
    train_rights = [] #记录训练数据集准确率的容器
    train_losses = []
    for batch_idx, (data, target) in enumerate(train_loader):  #针对容器中的每一个批进行循环
        data, target = Variable(data), Variable(target) #将Tensor转化为Variable，data为图像，target为标签
        #如果存在GPU则将变量加载到GPU中
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        output = net(data) #完成一次预测
        loss = criterion(output, target) #计算误差
        optimizer.zero_grad() #清空梯度
        loss.backward() #反向传播
        optimizer.step() #一步随机梯度下降
        right = rightness(output, target) #计算准确率所需数值，返回正确的数值为（正确样例数，总样本数）
        train_rights.append(right) #将计算结果装到列表容器中
        loss = loss.cpu() if use_cuda else loss
        train_losses.append(loss.data.numpy())


        #if batch_idx % 20 == 0: #每间隔100个batch执行一次
     #train_r为一个二元组，分别记录训练集中分类正确的数量和该集合中总的样本数
    train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))

    #在测试集上分批运行，并计算总的正确率
    net.eval() #标志模型当前为运行阶段
    test_loss = 0
    correct = 0
    vals = []
    #对测试数据集进行循环
    for data, target in val_loader:
        #如果存在GPU则将变量加载到GPU中
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        data, target = Variable(data, requires_grad=True), Variable(target)
        output = net(data) #将特征数据喂入网络，得到分类的输出
        val = rightness(output, target) #获得正确样本数以及总样本数
        vals.append(val) #记录结果

    #计算准确率
    val_r = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
    val_ratio = 1.0*val_r[0].numpy()/val_r[1]

    if val_ratio > best_r:
        best_r = val_ratio
        best_model = copy.deepcopy(net)
    #打印准确率等数值，其中正确率为本训练周期Epoch开始后到目前撮的正确率的平均值
    print('训练周期: {} \tLoss: {:.6f}\t训练正确率: {:.2f}%, 校验正确率: {:.2f}%'.format(
        epoch, np.mean(train_losses), 100. * train_r[0].numpy() / train_r[1], 100. * val_r[0].numpy()/val_r[1]))       
    record.append([np.mean(train_losses), 1. * train_r[0].data.numpy() / train_r[1], 1. * val_r[0].data.numpy() / val_r[1]])

#绘制训练误差曲线
x = [x[0] for x in record]
y = [1 - x[1] for x in record]
z = [1 - x[2] for x in record]
#plt.plot(x)
plt.figure(figsize = (10, 7))
plt.plot(y)
plt.plot(z)
plt.xlabel('Epoch')
plt.ylabel('Error Rate')

测试模型，绘制分类效果

def visualize_model(model, num_images=6):
    images_so_far = 0
    fig = plt.figure(figsize=(15,10))

    for i, data in enumerate(val_loader):
        inputs, labels = data
        inputs, labels = Variable(inputs), Variable(labels)
        if use_cuda:
            inputs, labels = inputs.cuda(), labels.cuda()
        outputs = model(inputs)
        _, preds = torch.max(outputs.data, 1)
        preds = preds.cpu().numpy() if use_cuda else preds.numpy()
        for j in range(inputs.size()[0]):
            images_so_far += 1
            ax = plt.subplot( 2,num_images//2, images_so_far)
            ax.axis('off')

            ax.set_title('predicted: {}'.format(val_dataset.classes[preds[j]]))
            imshow(data[0][j])

            if images_so_far == num_images:
                return
visualize_model(net)

plt.ioff()
plt.show()

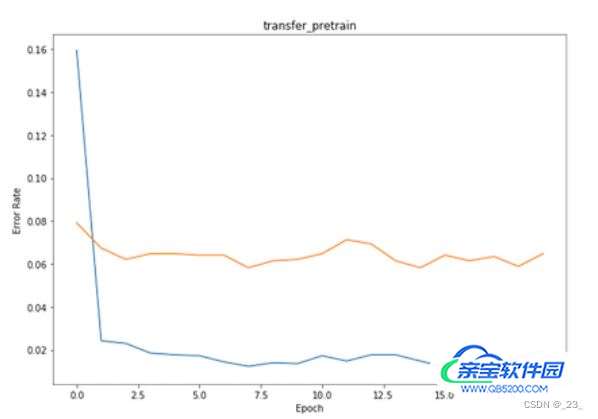
4.3.2.2 固定值模式

迁移过来的部分网络在结构和权重上都保持固定的数值不会改变。
要想让模型在固定值模式下训练，需要先锁定网络模型相关位置的参数。锁定的方法非常简单，只要把网络的梯度反传标志 requires_grad 设置为 False 就可以了。

# 加载residual网络模型
net = torchvision.models.resnet18(pretrained=True)
# 将模型放入GPU中
net = net.cuda() if use_cuda else net

# 循环网络，将所有参数设为不更新梯度信息
for param in net.parameters():
    param.requires_grad = False

# 将网络最后一层线性层换掉
num_ftrs = net.fc.in_features
net.fc = nn.Linear(num_ftrs, 2)
net.fc = net.fc.cuda() if use_cuda else net.fc

criterion = nn.CrossEntropyLoss() #Loss函数的定义
# 仅将线性层的参数放入优化器中
optimizer = optim.SGD(net.fc.parameters(), lr = 0.001, momentum=0.9)


#训练模型
record = [] #记录准确率等数值的容器

#开始训练循环
num_epochs = 4
net.train(True) # 给网络模型做标记，标志说模型在训练集上训练
best_model = net
best_r = 0.0
for epoch in range(num_epochs):
    #optimizer = exp_lr_scheduler(optimizer, epoch)
    train_rights = [] #记录训练数据集准确率的容器
    train_losses = []
    for batch_idx, (data, target) in enumerate(train_loader):  #针对容器中的每一个批进行循环
        data, target = Variable(data), Variable(target) #将Tensor转化为Variable，data为图像，target为标签
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        output = net(data) #完成一次预测
        loss = criterion(output, target) #计算误差
        optimizer.zero_grad() #清空梯度
        loss.backward() #反向传播
        optimizer.step() #一步随机梯度下降
        right = rightness(output, target) #计算准确率所需数值，返回正确的数值为（正确样例数，总样本数）
        train_rights.append(right) #将计算结果装到列表容器中
        loss = loss.cpu() if use_cuda else loss
        train_losses.append(loss.data.numpy())


     #train_r为一个二元组，分别记录训练集中分类正确的数量和该集合中总的样本数
    train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))

    #在测试集上分批运行，并计算总的正确率
    net.eval() #标志模型当前为运行阶段
    test_loss = 0
    correct = 0
    vals = []
    #对测试数据集进行循环
    for data, target in val_loader:
        data, target = Variable(data, requires_grad=True), Variable(target)
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        output = net(data) #将特征数据喂入网络，得到分类的输出
        val = rightness(output, target) #获得正确样本数以及总样本数
        vals.append(val) #记录结果

    #计算准确率
    val_r = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
    val_ratio = 1.0*val_r[0].numpy()/val_r[1]

    if val_ratio > best_r:
        best_r = val_ratio
        best_model = copy.deepcopy(net)
    #打印准确率等数值，其中正确率为本训练周期Epoch开始后到目前撮的正确率的平均值
    print('训练周期: {} \tLoss: {:.6f}\t训练正确率: {:.2f}%, 校验正确率: {:.2f}%'.format(
        epoch, np.mean(train_losses), 100. * train_r[0].numpy() / train_r[1], 100. * val_r[0].numpy()/val_r[1]))       
    record.append([np.mean(train_losses), 1. * train_r[0].data.numpy() / train_r[1], 1. * val_r[0].data.numpy() / val_r[1]])


# 绘制误差曲线
x = [x[0] for x in record]
y = [1 - x[1] for x in record]
z = [1 - x[2] for x in record]
#plt.plot(x)
plt.figure(figsize = (10, 7))
plt.plot(y)
plt.plot(z)
plt.xlabel('Epoch')
plt.ylabel('Error Rate')


#展示分类结果
visualize_model(best_model)

plt.ioff()
plt.show()

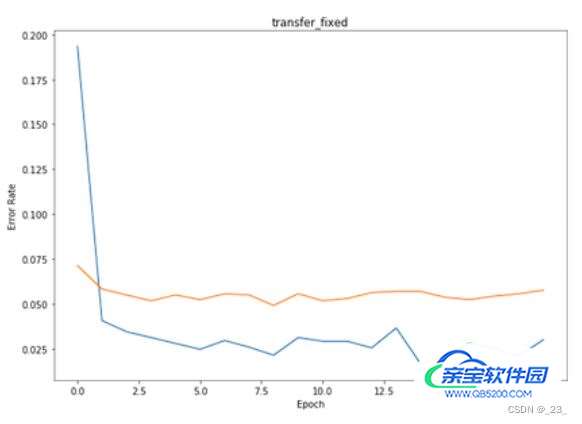
4.4 结论

该实验中，预训练迁移模型取得的效果整体的错误率比简单卷积神经网络低了很多。训练错误率可以稳定在 0.02 之下，测试错误率大约在 0.07 左右。因为在预训练模式下，模型对训练数据的拟合性比较强，所以训练错误率与测试错误率差别较大。
在固定值迁移模式下，训练错误率可以在 0.02 ~ 0.04 之间，比预训练模式稍高。测试错误率大约在 0.07 左右，与预训练模式差不多。
因为固定值模式锁定了大部分权重，模型对训练数据的拟合性没那么强，所以训练错误率与测试错误率的差别也没那么大。

加载全部内容