Python常用队列全面详细梳理
杨jun坚 人气:0一,队列
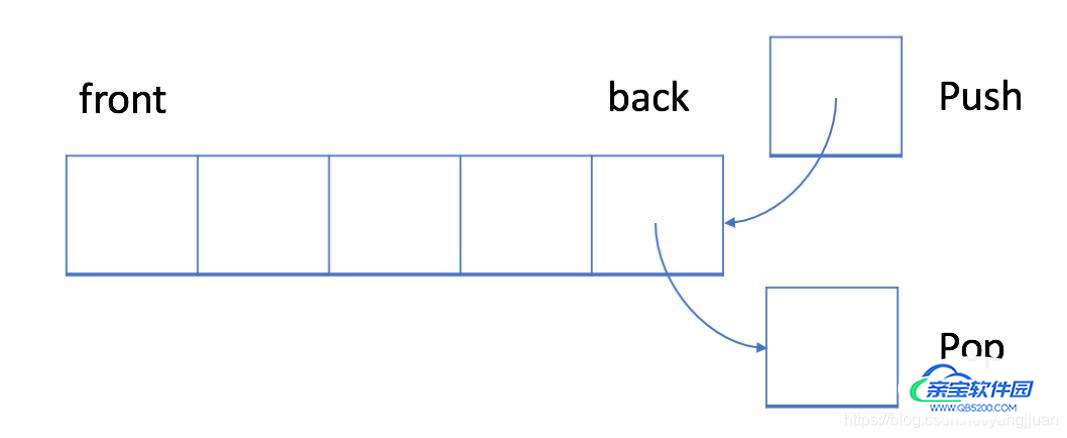
和栈一样,队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作。队列是一种操作受限制的线性表,进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
二,常见队列
1,FIFO队列
基本FIFO队列 先进先出 FIFO即First in First Out,先进先出。

调用queue.Queue
from queue import Queue fifo_queue = Queue() fifo_queue.put(1) # 队尾插入新元素 fifo_queue.put(2) fifo_queue.put(3) print(fifo_queue.queue) print(fifo_queue.get()) # 队头取出元素 print(fifo_queue.queue)
链表实现
class LNode(object):
def __init__(self, item, next_=None):
self.item = item
self.next = next_
class FIFOQueue(object):
def __init__(self):
"""初始化"""
self.head = None
self.rear = None
def is_empty(self):
"""判断是否为空"""
return self.head is None
def size(self):
"""获取队列长度"""
cur = self.head
count = 0
while True:
count += 1
if cur == self.rear:
break
cur = cur.next
return count
def travel(self):
"""遍历队列"""
if self.is_empty():
print('queue is empty')
return
else:
cur = self.head
while True:
print(cur.item, end='')
if cur.next:
print(',', end='')
if cur == self.rear:
break
cur = cur.next
print('')
def push(self, val):
"""队尾插入新元素"""
p = LNode(val)
if self.is_empty():
self.head = p
self.rear = p
else:
self.rear.next = p
self.rear = self.rear.next
def get(self):
"""获取队头元素"""
if self.is_empty():
print('queue is empty')
return
else:
e = self.head.item
self.head = self.head.next
return e
if __name__ == '__main__':
FIFOQueue = FIFOQueue()
FIFOQueue.push(1)
FIFOQueue.push(2)
FIFOQueue.push(3)
FIFOQueue.push(4)
FIFOQueue.travel() # 1,2,3,4
print(FIFOQueue.get()) # 1
print(FIFOQueue.get()) # 2
FIFOQueue.travel() # 3,4
list实现
# list 实现
class FIFOQueue(object):
def __init__(self):
self.queue = list()
def size(self):
return len(self.queue)
def travel(self):
print(self.queue)
def push(self, val):
self.queue.append(val)
def get(self):
return self.queue.pop(0)
if __name__ == '__main__':
FIFOQueue = FIFOQueue()
FIFOQueue.push(1)
FIFOQueue.push(2)
FIFOQueue.push(3)
FIFOQueue.push(4)
FIFOQueue.travel() # 1,2,3,4
print(FIFOQueue.get()) # 1
print(FIFOQueue.get()) # 2
FIFOQueue.travel() # 3,4
2,LIFO队列
LIFO即Last in First Out,后进先出。与栈的类似,在队尾进行插入和删除操作。
调用queue.LifoQueue
from queue import LifoQueue lifo_queue = LifoQueue() lifo_queue.put(1) # 队尾插入新元素 lifo_queue.put(2) lifo_queue.put(3) print(lifo_queue.queue) print(lifo_queue.get()) # 队尾取出元素 print(lifo_queue.queue)
链表实现
将链表头部作为队列尾部,在链表头部进行插入和删除操作。
class LNode(object):
def __init__(self, item, next_=None):
self.item = item
self.next = next_
class LIFOQueue(object):
def __init__(self):
"""初始化"""
self.head = None
def is_empty(self):
"""判断是否为空"""
return self.head is None
def size(self):
"""获取队列长度"""
cur = self.head
count = 0
while cur:
count += 1
cur = cur.next
return count
def travel(self):
"""遍历队列"""
travel_list = []
cur = self.head
while cur:
travel_list.append(cur.item)
cur = cur.next
travel_list.reverse()
print(travel_list)
def push(self, val):
"""头部插入"""
self.head = LNode(val, self.head)
def get(self):
"""获取队头元素"""
if self.is_empty():
print('queue is empty')
return
else:
e = self.head.item
self.head = self.head.next
return e
if __name__ == '__main__':
LIFOQueue = LIFOQueue()
LIFOQueue.push(1)
LIFOQueue.push(2)
LIFOQueue.push(3)
LIFOQueue.push(4)
LIFOQueue.travel() # 1,2,3,4
print(LIFOQueue.get()) # 4
print(LIFOQueue.get()) # 3
LIFOQueue.travel() # 1,2
List实现
# list 实现
class LIFOQueue(object):
def __init__(self):
self.queue = list()
def size(self):
return len(self.queue)
def travel(self):
print(self.queue)
def push(self, val):
self.queue.append(val)
def get(self):
return self.queue.pop()
if __name__ == '__main__':
LIFOQueue = LIFOQueue()
LIFOQueue.push(1)
LIFOQueue.push(2)
LIFOQueue.push(3)
LIFOQueue.push(4)
LIFOQueue.travel() # 1,2,3,4
print(LIFOQueue.get()) # 4
print(LIFOQueue.get()) # 3
LIFOQueue.travel() # 1,2
3,双向队列
双端队列(deque,全名 double-ended queue),是一种具有队列和栈的性质的数据结构。双端队列中的元素可以从两端弹出,其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。

调用collections .deque
collections 是 python 内建的一个集合模块,里面封装了许多集合类,其中队列相关的集合只有一个:deque。
deque 是双边队列(double-ended queue),具有队列和栈的性质,在 list 的基础上增加了移动、旋转和增删等。
deque(maxlen=3),通过maxlen参数,可以创建固定长度的队列,当新元素加入队列且队列已满,会自动从另一端移除首个元素。不指定maxlen,得到无界限的队列。
from collections import deque
d = deque([])
d.append('a') # 在最右边添加一个元素,此时 d=deque('a')
print(d)
d.appendleft('b') # 在最左边添加一个元素,此时 d=deque(['b', 'a'])
print(d)
d.extend(['c', 'd']) # 在最右边添加所有元素,此时 d=deque(['b', 'a', 'c', 'd'])
print(d)
d.extendleft(['e', 'f']) # 在最左边添加所有元素,此时 d=deque(['f', 'e', 'b', 'a', 'c', 'd'])
print(d)
d.pop() # 将最右边的元素取出,返回 'd',此时 d=deque(['f', 'e', 'b', 'a', 'c'])
print(d)
d.popleft() # 将最左边的元素取出,返回 'f',此时 d=deque(['e', 'b', 'a', 'c'])
print(d)
d.rotate(-2) # 向左旋转两个位置(正数则向右旋转),此时 d=deque(['a', 'c', 'e', 'b'])
print(d)
双向链表实现

class DLNode(object):
def __init__(self, item, prior_=None, next_=None):
self.item = item
self.prior = prior_
self.next = next_
class DQueue(object):
def __init__(self):
self.head = None # 头指针
self.rear = None # 尾制造
def is_empty(self):
return self.head is None
def length(self):
if self.is_empty():
print('queue is empty')
return
else:
cur = self.head
count = 0
while True:
count += 1
if cur == self.rear:
break
cur = cur.next
return count
def travel(self):
"""遍历队列"""
if self.is_empty():
print('queue is empty')
return
else:
cur = self.head
while True:
print(cur.item, end='')
if cur.next:
print(',', end='')
if cur == self.rear:
break
cur = cur.next
print('')
def push_rear(self, val):
"""队尾插入元素"""
p = DLNode(val)
if self.is_empty():
self.head = p
self.rear = p
else:
self.rear.next = p
p.prior = self.rear
self.rear = self.rear.next
def push_head(self, val):
"""队头插入元素"""
p = DLNode(val)
if self.is_empty():
self.head = p
self.rear = p
else:
p.next = self.head
self.head.prior = p
self.head = p
def pop_rear(self):
"""获取队尾元素"""
if self.is_empty():
print('queue is empty')
return
else:
p = self.rear
self.rear = self.rear.prior
self.rear.next = None
return p.item
def pop_head(self):
"""获取队头元素"""
if self.is_empty():
print('queue is empty')
return
else:
e = self.head.item
self.head = self.head.next
return e
if __name__ == '__main__':
DQueue = DQueue()
DQueue.push_head(1)
DQueue.push_head(2)
DQueue.push_head(3)
DQueue.travel() # 3,2,1
DQueue.push_rear('a')
DQueue.push_rear('b')
DQueue.travel() # 3,2,1,a,b
print(DQueue.pop_head()) # 3
print(DQueue.pop_rear()) # b
print(DQueue.pop_rear()) # a
DQueue.travel() # 2,1list实现
class DQueue:
"""双端队列"""
def __init__(self):
self.queue = []
def push_head(self, val):
"""从队头加入一个元素"""
self.queue.insert(0, val)
def push_rear(self, val):
"""从队尾加入一个元素"""
self.queue.append(val)
def pop_head(self):
"""从队头删除一个元素"""
return self.queue.pop(0)
def pop_rear(self):
"""从队尾删除一个元素"""
return self.queue.pop()
def is_empty(self):
"""是否为空"""
return self.queue == []
def size(self):
"""队列长度"""
return len(self.queue)
def travel(self):
print(self.queue)
if __name__ == "__main__":
DQueue = DQueue()
DQueue.push_head(1)
DQueue.push_head(2)
DQueue.push_head(3)
DQueue.travel() # [3, 2, 1]
DQueue.push_rear('a')
DQueue.push_rear('b')
DQueue.travel() # [3, 2, 1, 'a', 'b']
print(DQueue.pop_head()) # 3
print(DQueue.pop_rear()) # b
print(DQueue.pop_rear()) # a
DQueue.travel() # [2, 1]4,优先级队列

优先级队列是一种容器型数据结构,它能管理一队记录,并按照排序字段(例如一个数字类型的权重值)为其排序。由于是排序的,所以在优先级队列中你可以快速获取到最大的和最小的值。
可以认为优先级队列是一种修改过的普通队列:普通队列依据记录插入的时间来获取下一个记录,而优先级队列依据优先级来获取下一个记录,优先级取决于排序字段的值。
优先级队列常用来解决调度问题,比如给紧急的任务更高的优先级。以操作系统的任务调度为例:高优先级的任务(比如实时游戏)应该先于低优先级的任务(比如后台下载软件更新)执行。
调用queue.PriorityQueue
在 Python 中,内置的标准库提供了两种实现优先队列的数据结构,分别是 heapq 模块和 PriorityQueue 模块,
最小优先级队列
更小的值具有更高的优先级,也就是会被最先输出
# 优先级队列
from queue import PriorityQueue as PQ
Pqueue = PQ()
Pqueue.put((1, 'a'))
Pqueue.put((3, 'c'))
Pqueue.put((2, 'b'))
Pqueue.put((2, 'd'))
Pqueue.put((5, 'e'))
print(Pqueue.queue) # [(1, 'a'), (2, 'd'), (2, 'b'), (3, 'c'), (5, 'e')]
while not Pqueue.empty():
print(Pqueue.get())
# (1, 'a')
# (2, 'b')
# (2, 'd')
# (3, 'c')
# (5, 'e')
最大优先级队列
更大的值具有更高的优先级,也就是会被最先输出。
from queue import PriorityQueue as PQ
Pqueue = PQ()
Pqueue.put((-1, 'a'))
Pqueue.put((-3, 'c'))
Pqueue.put((-2, 'b'))
Pqueue.put((-2, 'd'))
Pqueue.put((-5, 'e'))
print(Pqueue.queue) # [(-5, 'e'), (-3, 'c'), (-2, 'b'), (-1, 'a'), (-2, 'd')]
while not Pqueue.empty():
print(Pqueue.get())
# (-5, 'e')
# (-3, 'c')
# (-2, 'b')
# (-2, 'd') 当两个对象的优先级一致时,按照插入顺序排列
# (-1, 'a')
基于 heapq 实现
heapq 涉及到另一种数据结构“堆”,用heapq 实现优先级队列,也是基于最小堆,最大堆实现,这些在后面“堆”再一起研究下。
import heapq
class PriorityQueue(object):
def __init__(self):
self._queue = []
# self._index = 0
def push(self, item, priority):
"""
队列由 (priority, index, item) 形式组成
priority 默认是最小优先级,增加 "-" 实现最大优先级,
index 是为了当两个对象的优先级一致时,按照插入顺序排列
"""
heapq.heappush(self._queue, (-priority, item))
# self._index += 1
def pop(self):
"""
弹出优先级最高的对象
"""
return heapq.heappop(self._queue)[-1]
def qsize(self):
return len(self._queue)
def empty(self):
return True if not self._queue else False
if __name__ == '__main__':
PQueue = PriorityQueue()
PQueue.push('a', 1)
PQueue.push('c', 3)
PQueue.push('b', 2)
PQueue.push('d', 2)
PQueue.push('e', 5)
PQueue.push('f', 1)
while not PQueue.empty():
print(PQueue.pop()) # e c b d a f
5,循环队列
在之前实现的队列时,都为固定队列长度,都创建无限队列,当队列空间有限时,插入和删除元素会有问题呢?
假定用长度为6的数组,表示长度为6的队列。队列中已经有三个元素a1、a2、a3。
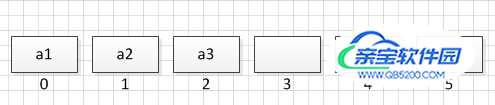
如果新插入元素,只需要在队尾插入便可,在下标3的位置插入新元素a4,入队列的时间复杂度O(1)。

如果删除元素,当a1出队列后,其后面的a2、a3、a4则需要向前移动一个位置,就好日常排队时,当前面人离开,后面的队伍都往前移动一步,所以出队列的时间复杂度为O(n)。

这种效率显然是不可以接受的,那么能不能不让所有成员都往前挪一位呢?
所以在原来的基础上,加入两个变量front、rear分别存储队头和队尾的下标。
此时front =0 ,rear = 3。
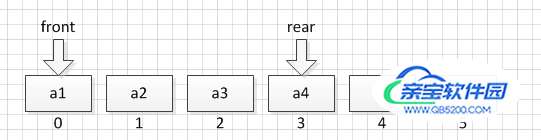
当有新元素插入队尾时,rear = rear+1。
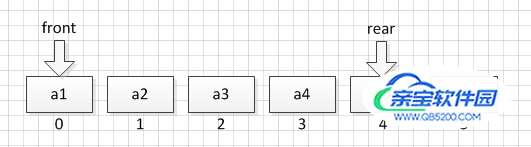
当有元素出队列时,front = front + 1
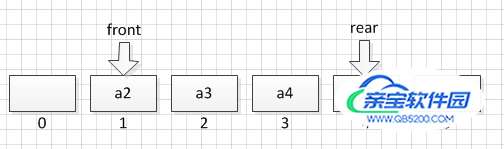
这样一来,似乎不将后面所有成员往前挪,只需维护一下front的指向(front += 1)就可以保证队首,但是,当遇到下面这情况时,就存在“假溢出”的情况。
将a2、a3都出队列,此时front = 3,在将a6插入队列,此时rear = 6。
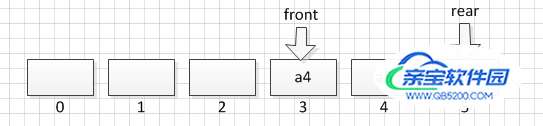
此时,队列长度为3,队列未满,再将a7插入队列时,就会报错数组越界,但是此时数组空间未满,前面0、1、2都空着,这种现象称为“假溢出”。
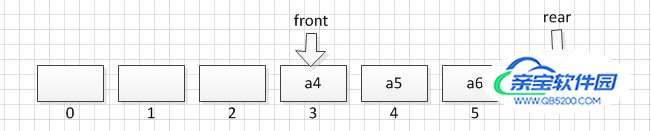
虽然这种方法不用移动元素,但是却造成空间上的浪费。可以看出此时数组是还有空间去容纳新元素a7的,因此我们需要将前面浪费的空间重新利用起来,减少空间的浪费,这就是循环队列的意义所在了。
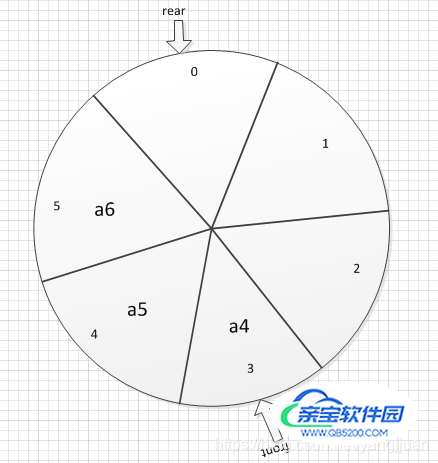
1.循环队列包括两个指针(其实就是两个整数型变量,因为在这里有指示作用,所以这里理解为指针), front 指针指向队头元素, rear 指针指向队尾元素的下一个位置。
2.rear和front互相追赶着,这个追赶过程就是队列添加和删除的过程,如果rear追到head说明队列满了,如果front追到rear说明队列为空。
3,rear和front位置的移动,关键在于% (取模运算),这样就防止rear和front 超过maxsize。
网上最常看到的实现代码
class SqQueue(object):
def __init__(self, maxsize):
self.queue = [None] * maxsize
self.maxsize = maxsize
self.front = 0
self.rear = 0
# 返回当前队列的长度
def QueueLength(self):
return (self.rear - self.front + self.maxsize) % self.maxsize
# 如果队列未满,则在队尾插入元素,时间复杂度O(1)
def EnQueue(self, data):
if (self.rear + 1) % self.maxsize == self.front:
print("The queue is full!")
else:
self.queue[self.rear] = data
# self.queue.insert(self.rear,data)
self.rear = (self.rear + 1) % self.maxsize
# 如果队列不为空,则删除队头的元素,时间复杂度O(1)
def DeQueue(self):
if self.rear == self.front:
print("The queue is empty!")
else:
data = self.queue[self.front]
self.queue[self.front] = None
self.front = (self.front + 1) % self.maxsize
return data
# 输出队列中的元素
def ShowQueue(self):
for i in range(self.maxsize):
print(self.queue[i],end=',')
print(' ')
这有个bug,由于 self.rear = (self.rear + 1) % self.maxsize 这会造成一个空间的浪费!! 可以运行下代码看看。
所以自己写了一段代码,直接使用现有元素个数cnt 与 maxsize 比较来判断是否为空?是否已满?
class CycleQueue(object):
def __init__(self, maxsize):
self.queue = [None] * maxsize
self.maxsize = maxsize
self.front = 0
self.rear = 0
self.cnt = 0
def is_empty(self):
return self.cnt == 0
def is_full(self):
return self.cnt == self.maxsize
def push(self, val):
if self.is_full():
print("The queue is full!")
return
if self.is_empty():
self.queue[self.rear] = val
self.cnt += 1
else:
self.rear = (self.rear + 1) % self.maxsize
self.queue[self.rear] = val
self.cnt += 1
def pop(self):
if self.is_empty():
print("The queue is empty!")
return
val = self.queue[self.front]
self.queue[self.front] = None
self.front = (self.front + 1) % self.maxsize
self.cnt -= 1
return val
def travel(self):
travel_list = [self.queue[(self.front + i) % self.maxsize] for i in range(self.cnt)]
print(travel_list)
def size(self):
return self.cnt
if __name__ == '__main__':
CycleQueue = CycleQueue(6)
CycleQueue.push('a1')
CycleQueue.push('a2')
CycleQueue.push('a3')
CycleQueue.push('a4')
CycleQueue.push('a5')
CycleQueue.travel() # ['a1', 'a2', 'a3', 'a4', 'a5']
CycleQueue.push('a6')
CycleQueue.travel() # ['a1', 'a2', 'a3', 'a4', 'a5', 'a6']
CycleQueue.pop()
CycleQueue.push('a7')
CycleQueue.travel() # ['a2', 'a3', 'a4', 'a5', 'a6', 'a7']
CycleQueue.pop()
CycleQueue.pop()
CycleQueue.push('a8')
CycleQueue.travel() # ['a4', 'a5', 'a6', 'a7', 'a8']
加载全部内容