C语言实现求解素数的N种方法总结
博客小梦 人气:0前言
哈喽各位友友们,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!我仅已此文,手把手带领大家探讨利用试除法、筛选法求解素数的n层境界!都是精华内容,可不要错过哟!!!
必备小知识
质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)。这里以求解100~200之间的素数举例讲解
C语言详解《试除法》求解素数
试除法境界1
境界1实现思路分析:
- 首先,利用第一层for循环产生100~200的整数;
- 其次,利用第二层for循环产生2~ i - 1之间的整数,并让100到200之间的每一个数和2到 i - 1之间的整数试除。
- 定义flag变量,若flag为0,则不是素数;若flag为1,则是素数。
- 定义count变量,记录试除次数。
- 境界1算法的理性分析:境界1,简单来说就是让每一个数i和2~ i-1的数试除,这是最简单的想法,但是算法的效率是最低的~
看了文字的描述,大家可能理解的还是不够深刻。这里俺亲自敲出代码辅助大家理解~
境界1源码:
#include<stdio.h>
int main()
{
int count = 0;//记录试除次数
int i = 0;
int j = 0;
for (i = 100; i <= 200; i++)
{
int flag = 1;//flag最终结果为1,表示i是素数,为0表示不是素数。
for (j = 2; j < i; j++)
{
count++;
if (i % j == 0)
{
flag = 0;
break;
}
}
if(flag == 1)
printf("%d ", i);
}
printf("\n境界1试除总次数:%d", count);
return 0;
}
代码结果运行图:

由境界1求解100~200之间的素数,需要试除3292次!!!可见其算法效率如何啦。
试除法境界2
境界2实现思路分析:
- 首先利用第一层for循环产生101~199的整数,这是和境界1最本质的区别!为什么这样设计呢?原因很简单,因为100到200之间的偶数一定不是素数,可以不用参与试除过程。
- 其次,利用第二层for循环产生2~ i - 1之间的整数,并让101到199之间的每一个数和2到 i -1之间的整数试除。
- 定义flag变量,若flag为0,则不是素数;若flag为1,则是素数。
- 定义count变量,记录试除次数。
- 境界2算法的理性分析:境界2和境界1类似,就是让每一个数i和2~ i-1的数试除,但是境界2能够提前让一些本不可能是素数的整数(100—200间的偶数)提前排除掉~
境界2源码:
#include<stdio.h>
int main()
{
int count = 0;//记录试除次数
int i = 0;
int j = 0;
for (i = 101; i < 200; i+=2)//提前排除100到200之间的偶数,符合这个条件一定不是素数。
{
int flag = 1;//flag最终结果为1,表示i是素数,为0表示不是素数。
for (j = 2; j < i; j++)
{
count++;
if (i % j == 0)
{
flag = 0;
break;
}
}
if(flag == 1)
printf("%d ", i);
}
printf("\n境界2试除总次数:%d", count);
return 0;
}
代码结果运行图:
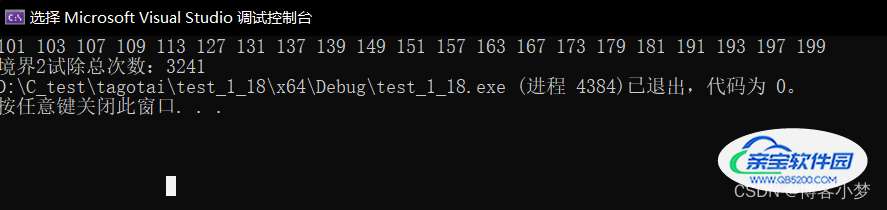
由境界2求解100~200之间的素数,需要试除3241次,稍微比境界1好那么一丢丢啦!但是其算法效率还是不尽人意。
试除法境界3
境界3实现思路分析:
- 首先,利用第一层for循环产生100~200的整数;
- 其次,利用第二层for循环产生2~ sqrt(i)之间的整数,并让101到199之间的每一个数和2到 sqrt(i)之间的整数试除。为什么这样设计呢?设计思路分析:因为任何一个不是素数的数即合数,都一定可以进行因式分解。这里已16举例说明,16 = 2 * 8 = 4 * 4 。因此如果16被2整除就可以判定16不是素数了,就不用那2到 i - 1的每一个数都试除一遍啦。 因此,只需要拿2 ~sqrt(i)的数试除即可,这样大大提高了算法的效率!
- 定义flag变量,若flag为0,则不是素数;若flag为1,则是素数。
- 定义count变量,记录试除次数。
- 境界3算法的理性分析:境界3相比于前面两种境界,做了很大的改进!让每一个数试除的测试减少了至少一半,大大减少了试除的次数,从而大大提高了算法的效率!!!
境界3源码:
#include<stdio.h>
#include<math.h>
int main()
{
int count = 0;//记录试除次数
int i = 0;
int j = 0;
for (i = 100; i <= 200; i++)
{
int flag = 1;//flag最终结果为1,表示i是素数,为0表示不是素数。
for (j = 2; j <= sqrt(i); j++)//只需要试除2到sqrt(i)之间的整数即可
{
count++;
if (i % j == 0)
{
flag = 0;
break;
}
}
if (flag == 1)
printf("%d ", i);
}
printf("\n境界3试除总次数:%d", count);
return 0;
}
代码结果运行图:
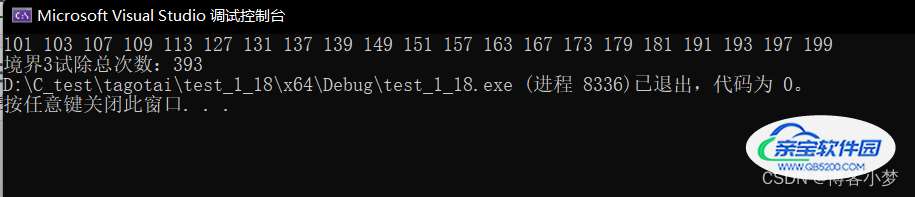
由境界4求解100~200之间的素数,只需要试除393次,相比于境界1和境界2的算法效率来说,已经有长足的改进啦!
试除法境界4
境界4实现思路分析:
- 首先,采用境界2的算法思想。利用第一层for循环产生101~199的整数。
- == 其次,利用境界三的试除想法,拿2 ~sqrt(i)的数试除。==
- 定义flag变量,若flag为0,则不是素数;若flag为1,则是素数。
- 定义count变量,记录试除次数。
- 境界4算法的理性分析:境界4相比于境界3,再做优化!先排除掉偶数。
境界4源码:
#include<stdio.h>
#include<math.h>
int main()
{
int count = 0;//记录试除次数
int i = 0;
int j = 0;
for (i = 101; i < 200; i += 2)//排除100到200之间的2的倍数,符合这个条件一定不是素数。
{
int flag = 1;//flag最终结果为1,表示i是素数,为0表示不是素数。
for (j = 2; j <= sqrt(i); j++)//只需要试除2到sqrt(i)之间的整数即可
{
count++;
if (i % j == 0)
{
flag = 0;
break;
}
}
if (flag == 1)
printf("%d ", i);
}
printf("\n境界4试除总次数:%d", count);
return 0;
}
代码结果运行图:
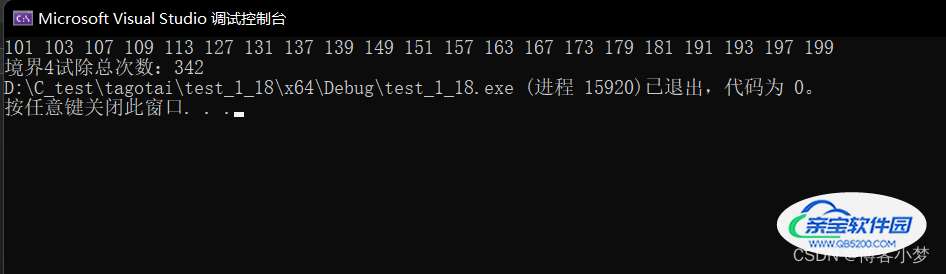
由境界4求解100~200之间的素数,试除总次数为342,是,综合考虑了境界2和境界3的改良思想,已经达到了试除法的最高境界啦!
C语言详解《筛选法》求解素数
预备小知识
埃拉托色尼是一名古希腊的地理学家,他是世界上第一个计算出地球周长的人。埃拉托色尼素数筛选法可以很快速的计算出1到N之间的所有素数。埃拉托色尼素数筛选法大概的计算思路是:将n开根号,即N^0.5 ,去掉2到N^0.5中所有素数的倍数,剩下的数便都是素数了。例如求1到25中的素数有哪些,第一步是将25开根号,得到5;第二步将2到5的素数取出来,分别是2、3、5:再将2到25中且是2、3、5的倍数的数去掉,即去掉4、6、8、9、10、12、14、15、16、18、 20、21、22、24、25;剩下2、3、5、7、11、13、17、19便是1到25中的所有素数了。从上面我们可以看出筛选法和试除法其实有着本质上的区别,试除法是判断每一个数是不是素数来达到目的;而筛选法不是如此,筛选法是将不是素数的数全部去除,然后得到余下的数来达到目的~
境界5(基础筛选法)实现思路分析:
- 首先,找到最小的质数2,再把范围内的所有2的倍数去掉;然后接下来找次小的质数3,再把所有3的倍数去掉;接着往复筛选去除,剩下的那些就全是素数啦!
- 这里需要设计一个数组,只要满足上述这些步骤,即将大于1的且是2、3、4…的倍数全部置为0。最终不是0的数就是所谓的素数啦!
筛选法境界5
境界5源码:
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int arr[100];
int count = 0;
for (i = 0; i < 100; i++)
{
arr[i] = 100 + i;//将数组先初始化存储100到199。
//没有存储200也没关系,200一定不是素数
}
for (i = 0; i < 100; i++)
{
j = i + 1;
while (j > 1)
{
count++;
if (arr[i] % j == 0)
arr[i] = 0;
j = j - 1;
}
}
for (j = 1; j < 100; j++)
{
if (arr[j] != 0)
{
printf("%d ", arr[j]);
}
}
return 0;
}代码结果运行图:

加载全部内容