一文读懂TS 中联合类型和交叉类型各自的含义

联合类型在 TypeScript 中相当流行，你可能已经用过很多次了。交叉类型稍微不那么常见。它们似乎引起更多的困惑。

你有没有想过这些名字是怎么来的？虽然你可能对两种类型的并集有一些直观感受，但交集通常不太容易理解。

阅读本文之后，你将对这些类型有更好的了解，这将使你在代码中使用它们时更有信心。

一、简单的联合类型

联合类型通常与 null 或 undefined 一起使用：

const sayHello = (name: string | undefined) => { /* ... */ };

例如，这里 name 的类型是 string | undefined 意味着可以将 string 或 undefined 的值传递给sayHello 函数。

sayHello("semlinker");
sayHello(undefined);

查看这个示例，你可以凭直觉知道类型 A 和类型 B 联合后的类型是同时接受 A 和 B 值的类型。

二、对象类型的并集和交集

这种直觉也适用于复杂类型。

interface Foo {
  foo: string;
  name: string;
}
 
interface Bar {
  bar: string;
  name: string;
}
 
const sayHello = (obj: Foo | Bar) => { /* ... */ };
 
sayHello({ foo: "foo", name: "lolo" });
sayHello({ bar: "bar", name: "growth" });

Foo | Bar 是含有 Foo 或 Bar 所有必须属性的类型。在 sayHello 内部只能访问 obj.name，因为它是两种类型都包含的唯一属性。

那么 Foo 和 Bar 类型的交集又怎么样？

const sayHello = (obj: Foo & Bar) => { /* ... */ };
 
sayHello({ foo: "foo", bar: "bar", name: "kakuqo" });

现在 sayHello 要求 obj 参数同时包含 foo 和 bar 的属性。所以在 sayHello 内部，有可能同时访问obj.foo，obj.bar 和 obj.name。

嗯，但是它有什么交集呢？有人可能会说，因为 obj 同时具有 Foo 和 Bar 的属性，所以它听起来更像是属性的并集，而不是交集。类似地，两个对象类型联合将得到一个类型，该类型只含有组成类型的属性的交集。

三、文氏图

文氏图（英语：Venn diagram），或译 Venn 图、温氏图、维恩图等，是在集合论（或者类的理论）数学分支中，在不太严格的意义下用以表示集合（或类）的一种草图。它们用于展示在不同的事物群组（集合）之间的数学或逻辑联系，尤其适合用来表示集合（或）类之间的 “大致关系”，它也常常被用来帮助推导（或理解推导过程）关于集合运算（或类运算）的一些规律。

在文氏图法中，如果有论域，则以一个矩形框（的内部区域）表示论域；各个集合（或类）就以圆／椭圆（的内部区域）来表示。两个圆／椭圆相交，其相交部分表示两个集合（或类）的公共元素，两个圆／椭圆不相交（相离或相切，而实际上在文氏图中相切是没有什么意义的，因为文氏图是以图形的内部区域来表示的）则说明这两个集合（或类）没有公共元素。

比如黄色的圆圈（集合 A）可以表示两足的所有动物。蓝色的圆圈（集合 B）可以表示会飞的所有动物。黄色和蓝色的圆圈交叠的区域（叫做交集）包含会飞且两足的所有动物 —— 比如鹦鹉。（把每个单独的动物类型想像为在这个图中的某个点）。

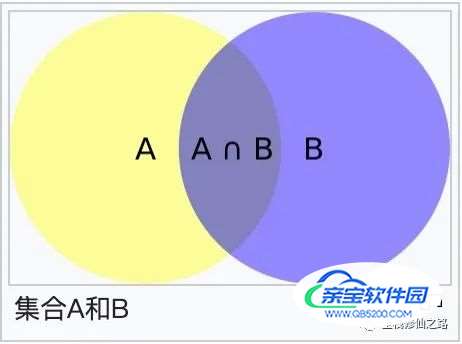
集合 A 和 B 的组合区域叫做集合 A 和 B 的并集。在这个示例中并集包含要么两足、要么会飞、要么两足并且会飞的所有东西。圆圈交叠暗示着两个集合的交集非空 —— 就是说在事实上有动物同时在黄色和蓝色圆圈中。

需要注意的是，文氏图与其它的图示法一样，它不能准确表示一个集合（或类）中到底有哪些元素。

四、集合理论

你还记得数学课中称为集合的概念吗？在数学中，集合是对象（例如数字）的集合。例如 {1, 2, 7} 是一组。所有正数也可以形成一组（无限个）。

可以将集合合并在一起（并集）。{1, 2} 和 {4, 5} 的并集是 {1, 2, 4, 5}。

集合也可以交叉。两个集合的交集是一个集合，它只包含两个集合中出现的那些数字。因此，{1, 2, 3} 和 {3, 4, 5} 的交集是 {3}。

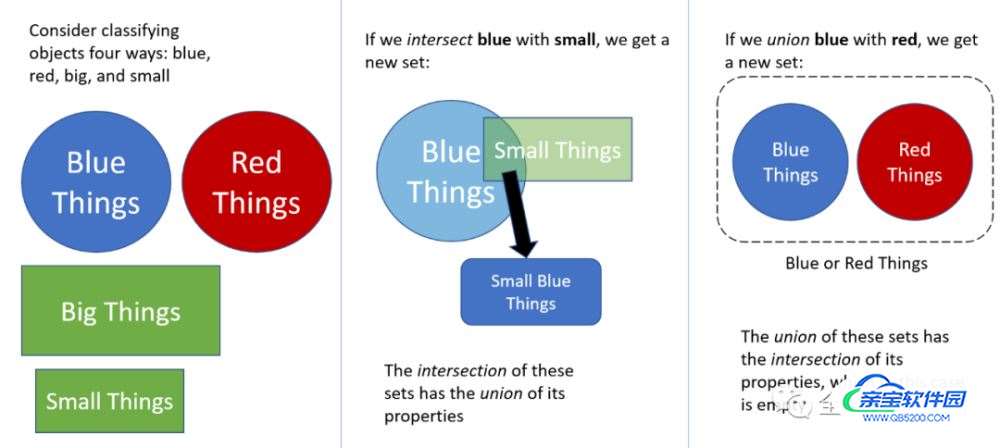
下面我们来换一种思考方式。假设有四个集合：红色的东西，蓝色的东西，大的东西，和小的东西。

如果你把所有红色的东西和所有小的东西的集合相交，你就得到了属性的并集 —— 集合里的所有东西都有红色的属性和小的属性。

但如果取红色小物体与蓝色小物体的并集，则结果集中只有小（small）属性是普遍存在的。“red small” 与  “blue small” 相交产生 “small”。

换句话说，取值域的并集会产生一组交叉的属性，反之亦然。具体过程如下图所示：

五、类型和集合之间的关系

计算机科学和数学在许多地方都有重叠。这样的地方之一就是类型系统。

从数学角度看，一种类型是该类型所有可能值的集合。例如，string 类型是所有可能的字符串的集合：{'a', 'b', 'ab', ...}。当然，这是一个无限的集合。同样，number 类型是一组所有可能的数字的集合：{1, 2, 3, 4, ...}。

类型 undefined 是一个仅包含单个值的集合：{ undefined }，该类型在 TypeScript 中被称为单元类型。

那么对象类型（比如接口）呢？类型 Foo 是包含 foo 和 name 属性的所有对象的集合。

六、了解联合类型和交叉类型

有了这些知识，你现在就可以了解联合和交叉类型的含义了。

联合类型 A | B 表示一个集合，该集合是与类型A关联的一组值和与类型 B 关联的一组值的并集。交叉类型 A & B 表示一个集合，该集合是与类型 A 关联的一组值和与类型 B 关联的一组值的交集。

因此，Foo | Bar 表示有 foo 和 name 属性的对象集和有 bar 和 name 属性的对象集的并集。属于这类集合的对象都含有 name 属性。有些有 foo 属性，有些有 bar 属性。

而 Foo & Bar 表示具有 foo 和 name 属性的对象集和具有 bar 和 name 属性的对象集的交集。换句话说，集合包含了属于由 Foo 和 Bar 表示的集合的对象。只有具有这三个属性（foo、bar 和 name）的对象才属于交集。

继续阅读：TypeScript 交叉类型

七、交叉类型的真实示例

联合类型非常普遍，所以让我们关注一个交叉类型的例子。

在 React 中，当你声明一个类组件时，可以使用它的属性类型对其进行参数化：

class Counter extends Component<CounterProps> { /* ... */ }

在类中，你可以通过 this.props 访问属性。然而， this.props 的类型不只是 CounterProps，而是：

Readonly<CounterProps> & Readonly<{ children?: ReactNode; }>

这样做的原因是 React 组件可以接收子元素：

<Counter><span>Hello Semlinker</span></Counter>

通过 children 属性可以访问到子元素。this.props 的类型反映了这一点。它是（readonly）CounterProps 和含有可选的 children 属性的（readonly）对象类型交集。

在集合方面，它是含有 CounterProps 中定义的属性的对象集和与含有可选 children 属性的对象集的交集。结果是一组含有 CounterProps 所有属性和可选 children 属性的对象集。

八、总结

本文为了帮助读者更好地理解 TypeScript 中的联合类型和交叉类型，我们引入了文氏图、集合理论及类型和集合之间的关系这些内容。计算机科学和数学在许多地方都有重叠，理解数学相关的基本原理后可以使你更好地掌握编程概念。

九、参考资源

• wiki - 文氏图
• The-meaning-of-union-and-interp-types
• naming-of-typescripts-union-and-interp-types