C语言数据结构中树与森林专项详解
莫浅子 人气:0树的存储结构
树的逻辑结构
树是n(n≥0)个结点的有限集合,n=0时,称为空树,这是一种特殊情况。在任意--棵非空树中应满足:
1)有且仅有一个特定的称为根的结点。
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集合T1,2....Tm,其中每个集合本身又是一-棵树,并且称为根结点的子树。
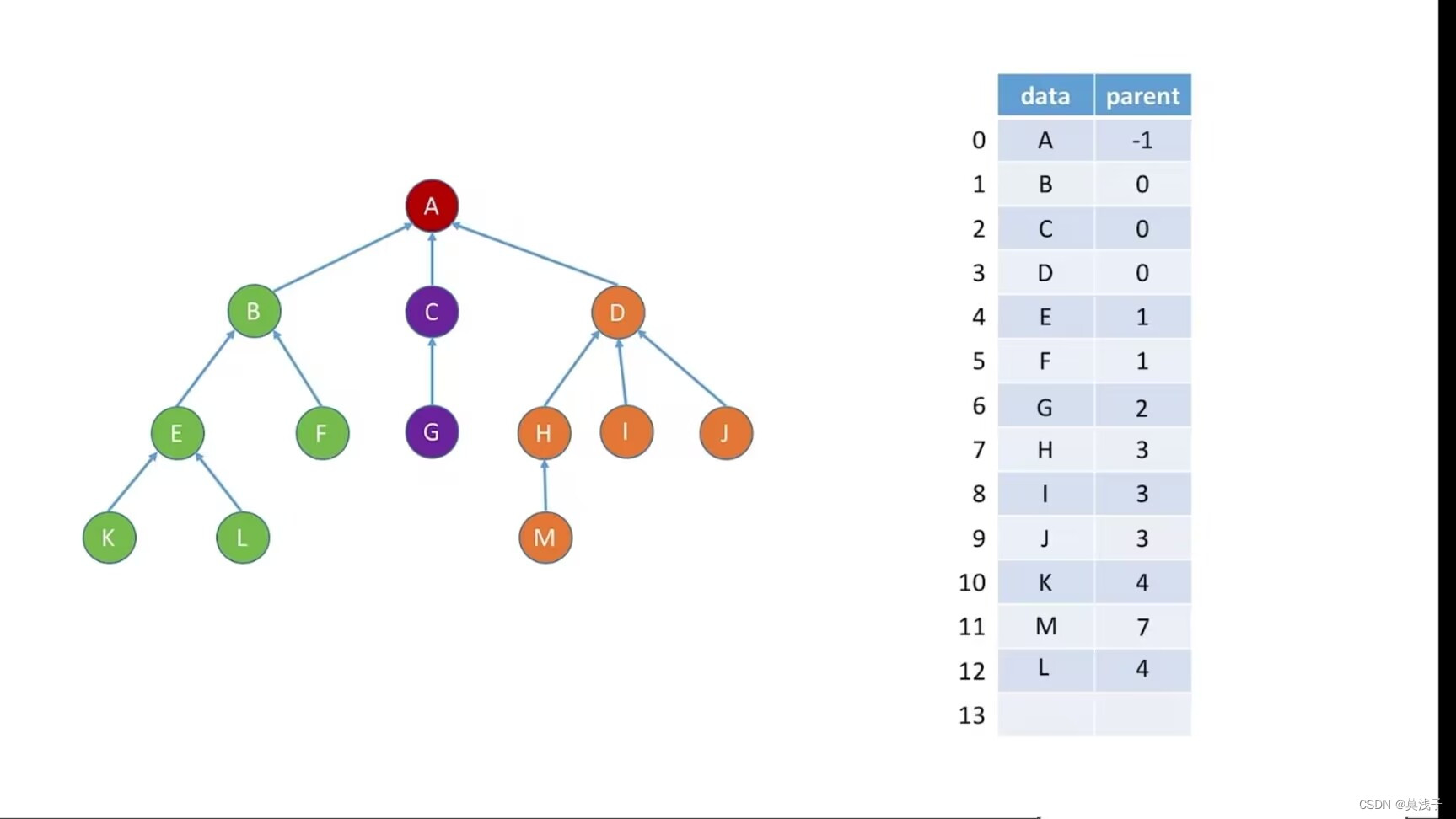
双亲表示法(顺序存储)
每个结点保存双亲的“指针”, 结点中保存父节点在数组的下标
优点:找父节点方便
缺点:找孩子不方便
删除元素方案一 ,数据删除后,parent 变为-1
删除元素方案二,数据删除后,将尾部数据填充到那
#define MAX_TREE_SIZE 100 //树中最多结点树
typedef struct{ //树的结点定义
Elemtype date; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MAX_TREE_SIZE]; //双亲表示
int n; //结点树
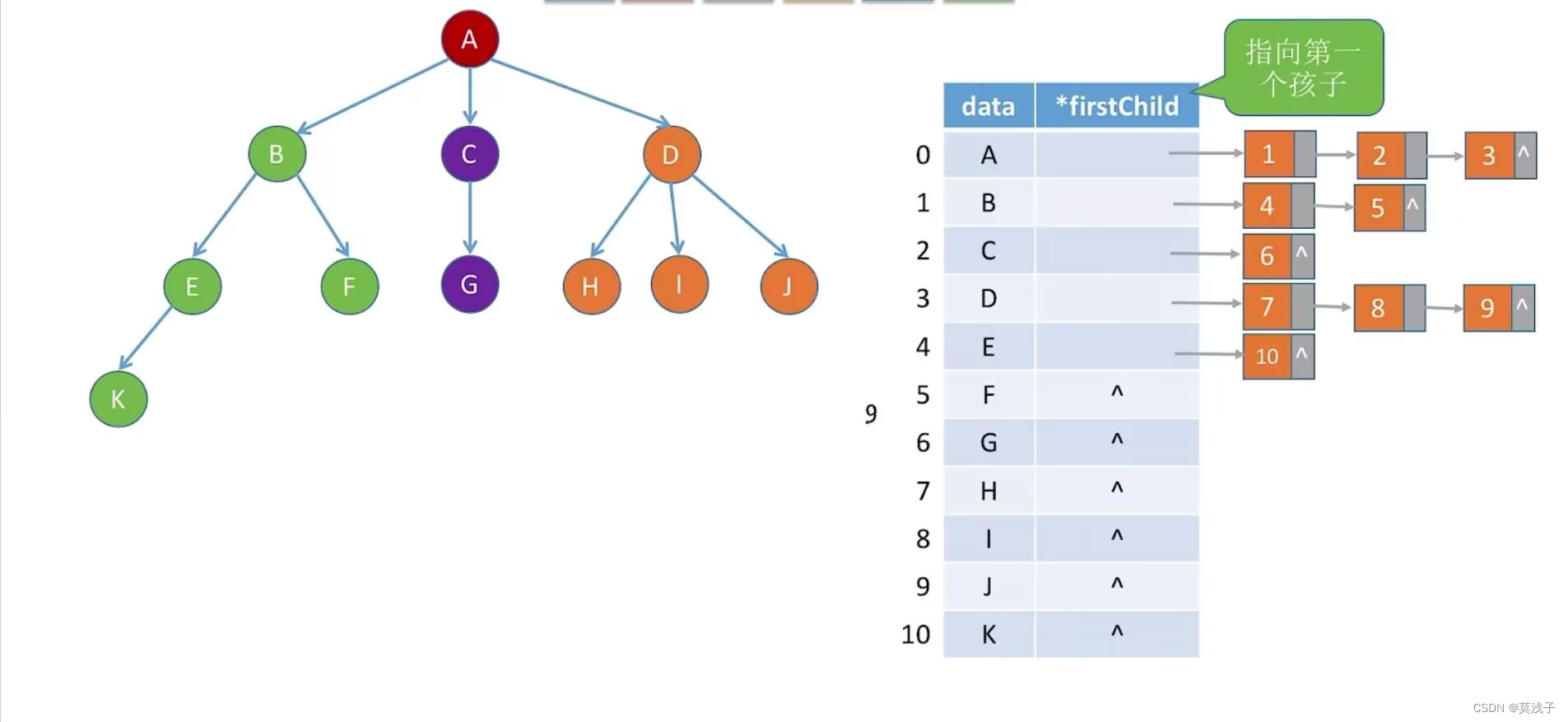
}PTree; 孩字表示法(顺序+链式存储)
顺序存储各个结点,每个结点保存孩子链表头指针
优点:找孩子方便
缺点:找双亲不方便
代码
#define MAX_TREE_SIZE 100 //树中最多结点树
typedef struct{ //树的结点定义
Elemtype date; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MAX_TREE_SIZE]; //双亲表示
int n; //结点树
}PTree;
struct CTNOde{
int child; //孩子结点在数组的位置
struct CTNode *next; //下一个孩子
}CTBox;
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n,r; //结点树和根的位置
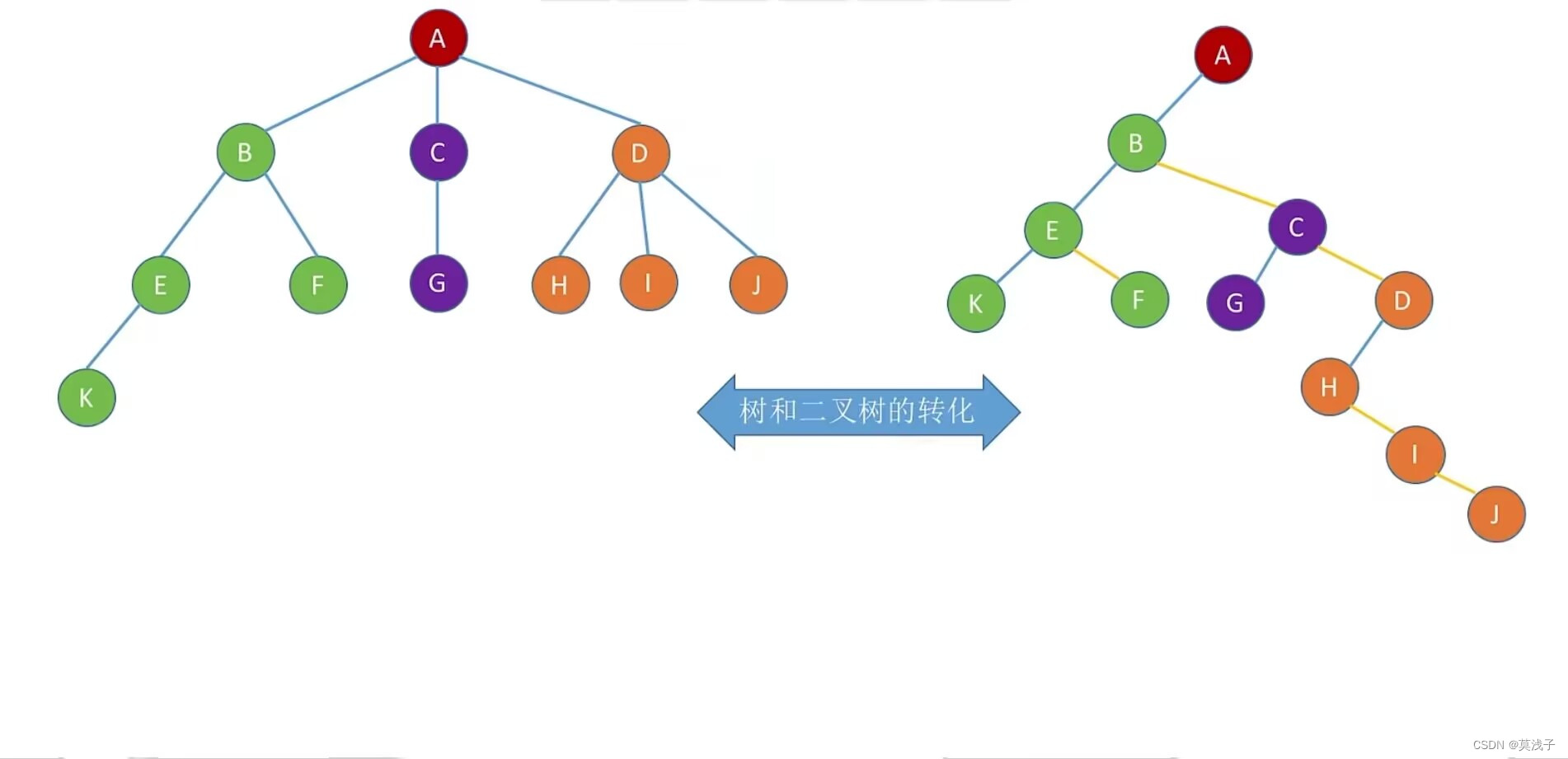
}; 孩子兄弟表示法(链式存储)
优点:可以用二叉树的操作来处理树
代码
//树的存储-孩子兄弟表示法
typedef struct CSDode{
Elemtype date; //数据域
struct CSDode *firstchild ,*nextsibling; //第一个孩子和右兄弟指针
}CSDode ,*CSTree; 森林
森林是m(m>=0)棵互不相交的树集合
森林中各个树的根结点之间是为兄弟关系
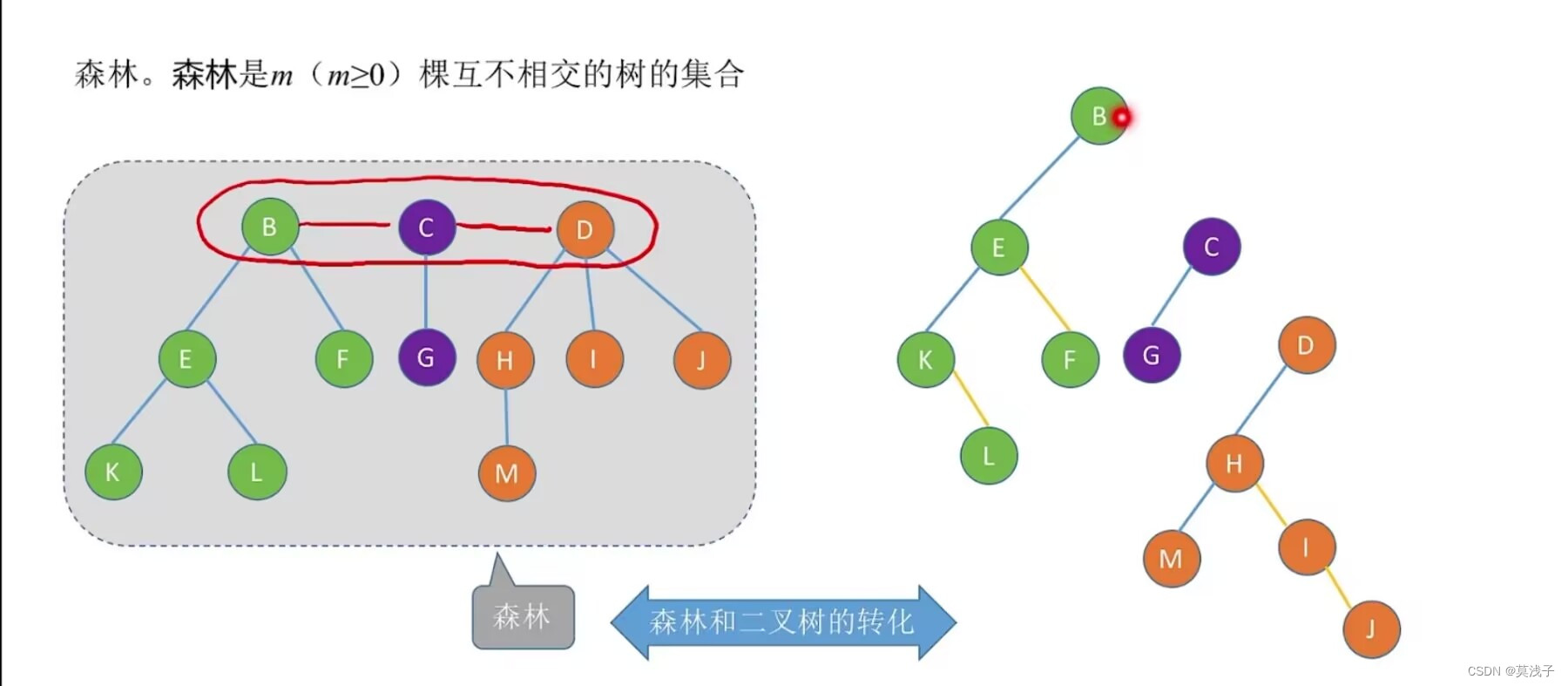
在二叉树中,如果是兄弟关系就在右边,如果是孩子就在左边,本质上,用二叉链表存储森林
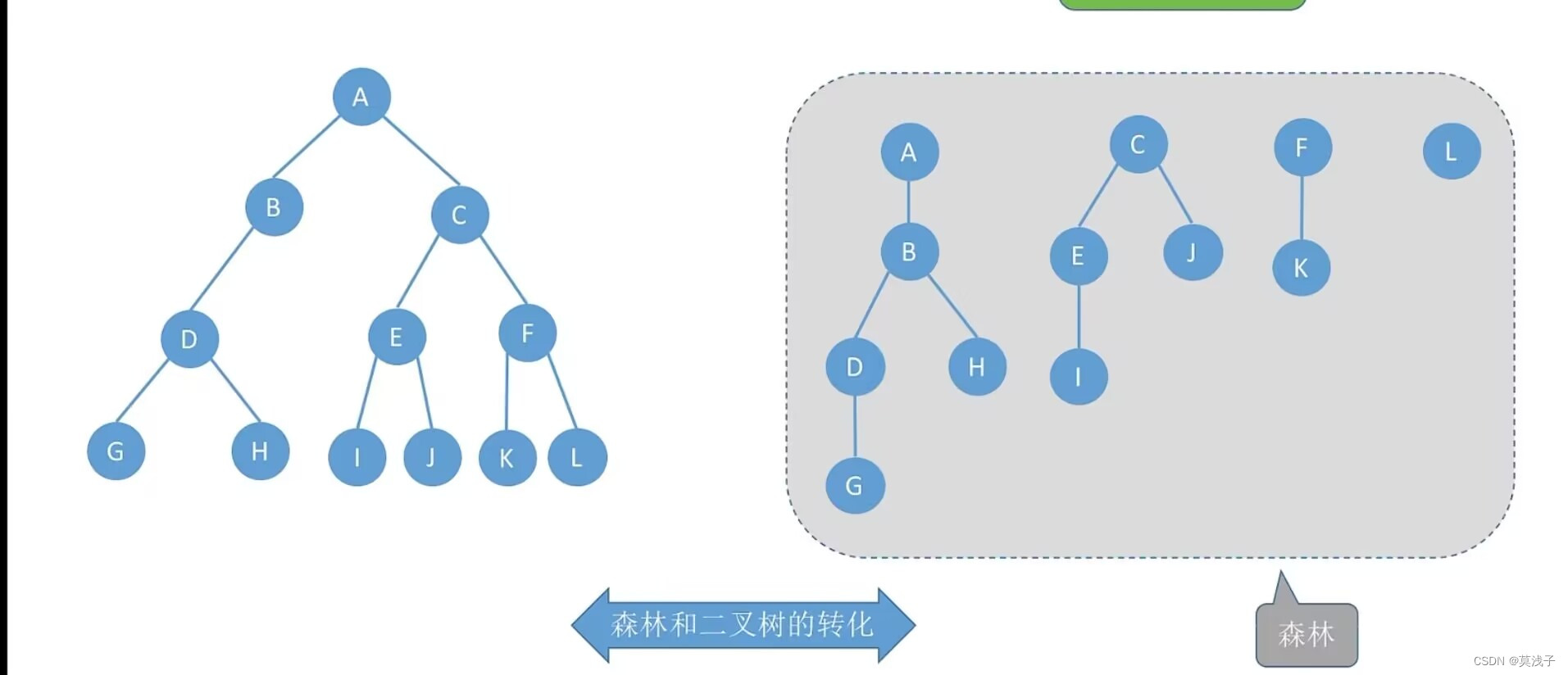
树的遍历

树的先根遍历(深度优先遍历)
先根遍历。若树非空,先访问根结点,在依次对没棵子树进行先根遍历。
上图这样一棵树的先根遍历顺序和二叉树的很像,按照二叉树的方法

//树的先根遍历
void PreOrder(TreeNode *R){
if(R!=NULL){
visit(R); //访问根结点
while(R还有下一个子树T)
PreOrder(T); //先根遍历下一棵子树
}
} 树的后根遍历(树的深度优先遍历)
若树非空,先依次对没棵子树进行后根遍历,最后在访问根结点
上图这样一棵树的后根遍历顺序和二叉树的很像,按照二叉树的方法
代码
//树的后根遍历
void PostOrder(TReeNode *R)
{
if(R != NULL){
while(R还有下一个子树T)
PodtOrder(T); //后根遍历下一棵子树
visit(R) //访问根结点
}
} 树的层序遍历(广度优先遍历)
层次遍历(用队列实现)
①若树非空,则根节点入队
②若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
③重复②直到队列为空
如图

森林的遍历
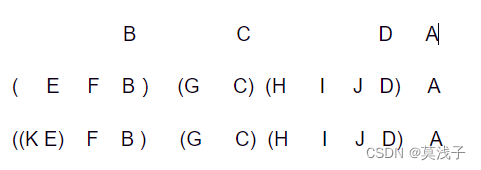
森林。森林是m (m>0)棵互不相交的树的集合。每棵树去掉根节点后,其各个子树又组成森林。
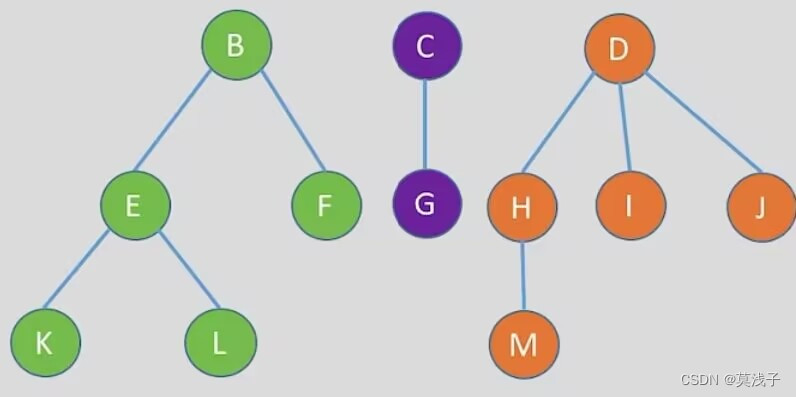
先序遍历森林
效果等同于依次对各二叉树进行先序遍历

若森林为非空,则按如下规则进行遍历:
1.访问森林中第一棵树的根结点
2.先序遍历第一棵树中根结点的子树森林。
3.先序遍历除去第一棵树之后剩余的树构成的森林。
效果如下

中序遍历森林
效果等同于依次对二叉树进行中序遍历

若森林为非空,则按如下规则进行遍历:
中序遍历森林中第一棵树的根结点的子树森林。
访问第一棵树的根结点。
中序遍历除去第一棵树之后剩余的树构成的森林。
效果如下

加载全部内容