React前端解链表数据结构示例详解

时间:2022-11-02 龙骑士尹道长人气:0

什么是链表

在面试中只要被问到React Hooks就常被问到为什么Hooks不能在循环和条件判断嵌套函数当中使用；相信很多人都知道标准答案，【因为声明的Hooks保存在链表当中】，但是你真的知道链表吗？

我们先看来看一个简单的单向链表结构

如上图所示我们可以分析出，链表是由多个 node(节点) 组成的，而node(节点) 指向(保存)不同的内存空间，每个node(节点) 由item(数据域) 和next(指针域) (双向链表还包括prev指针域)构成，其中item(数据域) 用于存储数据，next(指针域) 指向下一个节点从而形成一个存储数据的线性链路

总结：链表是一个用于存储数据的无序线性数据结构

而通过指针域指向链路的差异我们大致可以分为：

单向链表
双向链表
环形链表

链表与数组的比较

不知道链表这种数据结构能否让你想起数组，这两种都是用于存储数据的线性数据结构，而不同的是链表是一种无序线性数据结构，而数组是一种有序线性数据结构，我们都知道数组是一种引用类型数据结构，当我们创建一个数组的时候会在内存种开辟一串连续的内存空间用于存储，数组就是依靠这串连续的内存空间来维持线性链路，而链表则是有一连串无序的内存保存node(节点) 通过node(节点) 的指针域指向下一个节点来维持线性链路

链表有什么作用？

假设现在有一百条客户的数据你需要对这一百条数据进行增、删、插入你会怎么做？

创建一个数组将100条数据存入数组当中，通过数组的push，splice，findIndex，indexOf等方法对数组进行操作，对于少量数据答案是显而易见的，我们直接通过数组就能解决；但是如果现在有一百万条数据让你操作呢？我们已经提到数组是通过连续内存地址来维持线性链路的一种有序线性结构，如果你在头部插入一条数据的话则后面的一系列元素都要向后移动一位，一百万条数据则要移动一百万次，如果你要删除第一万个元素则后面的九十九万个元素要向前移动一个位置，如果要将第一条数据替换为最后一条数据则要先删除再插入先将第一条数据与最后一条数据取出其余所有数据要向前移动一个位(除头部数据与尾部数据)，然后再替换插入，所有数据再向后移动一位；在数据量庞大的情况下这绝对不是一个明智的方案，因为时间维度的不允许；但是如果换成链表你只需要操作node(节点) 指针域的指向便可以完成以上工作；

链表的优缺点

优点：相较于数组，链表操作更加的灵活，不受存储空间的限制；

缺点：

链表不能通过下标获取值，每次要获取链表当中的node(节点) 都需要经过遍历
对于存储基本类型的数据结构因为需要通过指针域的指向则需要多分配一块内存进行存储(双向链表则乘以2)

通过JS简单实现一个单向链表

而对于链表操作我们大致可以分为

新增
插入
删除
查看
修改

我们以单项链表为例依次实现他们

创建Node辅助类

我们已经知道链表的大致概念也就是链表是一种以多个node(节点) 通过指针域连接的无序线性数据结构，因此首先我们需要创建辅助类Node用于创建node(节点)

//辅助类Node用于创建保存在链表中的node
class Node {
    constructor (item) {
        //数据域，用于保存数据
        this.item = item
        //指针域，用于指向下一个节点
        this.next = null
    }
}

而在链表中始终有一个head属性，这个属性是链表的开端，用于存放整个链表的线性链路；我们还需要一个size用于保存链表的长度，用于遍历链表；

//用于创建一个链表
class Linked{
    constructor () {
        //size属性用于保存链表的长度用于遍历
        this.size = 0
        //用于存放线性链路
        this.head = null
    }
}

至此我们已经完成了创建一个链表的准备工作；那么让我们看看链表的基本操作方法是如何实现的

单向链表新增操作

对于单向链表新增如果当前链表为空我们需要将链表的head属性直接指向创建的node(节点)，如果链表不为空则我们需要将最末端的node(节点)的next(指针域) 指向新创建的 node(节点)

class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    //新增node方法
    add (item) {
        //创建node
        let node = new Node (item)
        //this.head === null则代表链表为空需要将新head指向新创建的node
        if (this.head === null) {
            this.head = node
        } else {
            //查找需要创建的节点的上一个节点(最末端节点)
            let prevNode = this.getNode (this.size - 1)
            //将末端节点的next指向新创建的node
            prevNode.next = node
        }
        //新增成功则size+1
        this.size++
    }
    //节点查找方法传入index类似于数组下标用于标记查找
    getNode (index) {
        //如果index < 0 || index >= this.size则说明下标越界需要在此限制
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        //获取第一个节点，从第一个节点进行遍历
        let current = this.head;
        for (let i = 0; i < index; i++) {
            //依次将当前节点指向下一个节点，直到获取最后一个节点
            current = current.next
        }
        return current
    }
}

单向链表插入操作

对于单向链表插入操作如果需要插入的位置为下标为0的位置(头部)，我们需要将需要插入的node(节点) 的next(指向域),指向未改变之前的第一个node(节点)，也就是head，如果是中间追加则我们需要将插入node（节点） 的指向域指向插入下标的上一个节点的指向域(插入节点的下一个节点)，并将插入node(节点) 的上一个节点的指向域，指向当前节点

class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    //追加插入
    //position为插入位置下标，item为需要保存到节点的元素
    insert (position, item) {
        //下标值越位判断
        if (position < 0 || position > this.size) {
            throw new Error ('Position out range');
        }
        //创建新节点
        let node = new Node (item)
        //头部追加
        //如果插入下标为0则直接将head指向新创建的节点
        if (position === 0) {
            node.next = this.head;
            this.head = node
        } else {//中间追加
            //获取追加节点的上一个节点
            let prevNode = this.getNode (position - 1)
            //将插入下标的指向域指向插入下标的上一个节点的指向指向域(下一个节点)
            node.next = prevNode.next
            //将插入下标的上一个节点的指向域，指向当前节点
            prevNode.next = node
        }
        //插入成功，长度加一
        this.size++
    }
    getNode (index) {
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next
        }
        return current
    }
}

单向链表删除操作

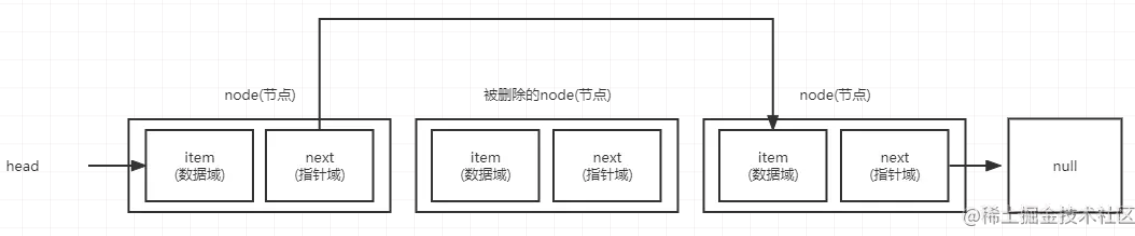
对于单向链表的删除操作，如果删除元素为链表的顶端元素则需要将head指向被删除元素的指针域（下一个元素），如果不是第一个元素则我们需要将上一个元素的指针域指向被删除元素的next（指针域）（下一个元素）

class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    delete (position) {
        //删除下标合法判断
        if (position < 0 || position >= this.size) {
            throw new Error ('position out range')
        }
        //获取当前链表（head）
        let linkList = this.head
        //如果删除的是链表的第一个元素则将head指向第一个元素的指针域（下一个元素）
        if (position === 0) {
            this.head = linkList.next;
        } else {//中间删除
            //获取删除元素的上一个节点
            let prevNode = this.getNode (position - 1)
            //将链表指向被删除元素上一个节点
            linkList = prevNode.next
            //将链表的的上一个节点指向被删除元素的下一个节点
            prevNode.next = linkList.next
        }
        //长度减一
        this.size--
    }
    getNode (index) {
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next
        }
        return current
    }
 }

单向链表查找操作

对于查找操作我们需要对链表进行遍历比对获取下标

class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    //查找指定元素下标
    findIndex (item) {
        //获取当前链表
        let current  = this.head
        //进行遍历操作依次比对获取查找元素下标
        for(let i=0;i<this.size;i++){
            if (current.item === item) {//如果current.item === item则说明该元素为需要查找的元素，返回下标
                return i
            }
            //使聊表指向他的下一个元素，使循环可以继续
           current = current.next
        }
        return null
    }
    getNode (index) {
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next
        }
        return current
    }
}

单向链表修改操作

对于单向链表的修改操作我们只需用下标获取需要修改的元素，并对其item重新进行赋值即可；

class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    getNode (index) {
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next
        }
        return current
    }
    //修改操作
    //position为需要修改元素的下标,item为修改的值
    update(position,item){
        let current = this.getNode(position)
        current.item = item
    }
}

单向链表类方法整合

class Node {
    constructor (item) {
        this.item = item
        this.next = null
    }
}
class Linked {
    constructor () {
        this.size = 0
        this.head = null
    }
    add (item) {
        let node = new Node (item)
        if (this.head === null) {
            this.head = node
        } else {
            let current = this.getNode (this.size - 1)
            current.next = node
        }
        this.size++
    }
    //追加插入
    insert (position, item) {
        //下标值越位判断
        if (position < 0 || position > this.size) {
            throw new Error ('Position out range');
        }
        //创建新节点
        let node = new Node (item)
        //头部追加
        //如果插入下标为0则直接将head指向新创建的节点
        if (position === 0) {
            node.next = this.head;
            this.head = node
        } else {//中间追加
            let prevNode = this.getNode (position - 1)
            //将插入下标的指向域指向插入下标的上一个节点的指向指向域(下一个节点)
            node.next = prevNode.next
            //将插入下标的上一个节点的指向域，指向当前节点
            prevNode.next = node
        }
        //插入成功，长度加一
        this.size++
    }
    delete (position) {
        //删除下标合法判断
        if (position < 0 || position >= this.size) {
            throw new Error ('position out range')
        }
        //获取当前链表（head）
        let linkList = this.head
        //如果删除的是链表的第一个元素则将head指向第一个元素的指针域（下一个元素）
        if (position === 0) {
            this.head = linkList.next;
        } else {//中间删除
            //获取删除元素的上一个节点
            let prevNode = this.getNode (position - 1)
            //将链表指向被删除元素上一个节点
            linkList = prevNode.next
            //将链表的的上一个节点指向被删除元素的下一个节点
            prevNode.next = linkList.next
        }
        //长度减一
        this.size--
    }
    //查找指定元素下标
    findIndex (item) {
        //获取当前链表
        let current  = this.head
        //进行遍历操作依次比对获取查找元素下标
        for(let i=0;i<this.size;i++){
            if (current.item === item) {//如果current.item === item则说明该元素为需要查找的元素，返回下标
                return i
            }
            //使聊表指向他的下一个元素，使循环可以继续
           current = current.next
        }
        return null
    }
    getNode (index) {
        if (index < 0 || index >= this.size) {
            throw new Error ('out range')
        }
        let current = this.head;
        for (let i = 0; i < index; i++) {
            current = current.next
        }
        return current
    }
    //修改操作
    //position为需要修改元素的下标,item为修改的值
    update(position,item){
        let current = this.getNode(position)
        current.item = item
    }
}

写在最后

对于链表的使用感受，我觉得我们不能将链表看成一个整体的数据结构，而是要将它单元化，通过指针域来灵活的使用它。其实我更加倾向于将链表理解成一种设计思路，我们也没必要将每个指针域命名为next，我们可以通过指针域的不同来构建千变万化的数据结构，它也可以拥有不止一个指针域，如果我们添加一个prev指针指向上一个节点那么这个链表就是一个双向链表，如果链表的最底层next指向的不是null而是当前链表中任意一个节点，那么它就是一个环形链表；当然我们也可以使一个节点拥有left和right两个指针域，指向不同的节点，那么它就是一个二叉树，甚至我们可以用链表的指针域概念来实现一个优先队列，虽然在前端开发中链表的操作非常少，但是在阅读源码当中我不止一次的看到链表这种数据结构。说白了，这是一个无用的知识，因为你在开发当中基本上用不到，但是链表的指针域概念却能提升你的思维，让你对数据结构有更广的思考；本来我是想再讲讲双向链表与环形链表的，但是我实在不知道如何用文字表达用快慢指针来判断环形链表中是否存在一个环，因此便没有继续；

加载全部内容