Python计算AUC

AUC（Area under curve）是机器学习常用的二分类评测手段，直接含义是ROC曲线下的面积，如下图：

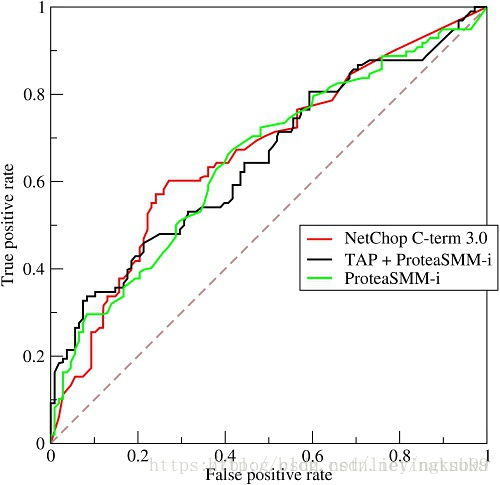
要理解这张图的含义，得先理解下面这个表：

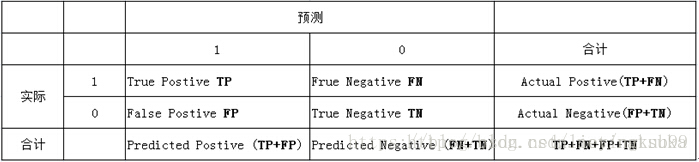
表中列代表预测分类，行代表实际分类：

• 实际1，预测1：真正类（tp）
• 实际1，预测0：假负类（fn）
• 实际0，预测1：假正类（fp）
• 实际0，预测0：真负类（tn）
• 真实负样本总数=n=fp+tn
• 真实正样本总数=p=tp+fn

在第一张图中，

横坐标false positive rate 代表假正类率，由fp/n计算得到，

意为 在实际负样本中出现预测正样本的概率。

纵坐标true positive rate 代表真正类率，由tp/p计算得到，

意为 在实际正样本中出现预测正样本的概率。

为什么这样一个指标可以衡量分类效果

先来看看如何得到这条曲线：

1. 通过分类器得到每个样本的预测概率，对其从高到低进行排序

2. 从高到低，分别以每一个预测概率作为阈值，大于该阈值的认定其为1，小于的为0，计算fp rate和tp rate。

对于一个有分类效果（效果比随机要好）的分类器，刚开始将高概率作为阈值时，阈值以上的真正样本占全部正样本的比例（tp rate）>阈值以上的假正样本占全部负样本的比例（fp rate）。

auc理解

auc就是：随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。

AUC计算

方法一

在有M个正样本,N个负样本的数据集里。一共有M*N对样本（一对样本即，一个正样本与一个负样本）。统计这M*N对样本里，正样本的预测概率大于负样本的预测概率的个数。

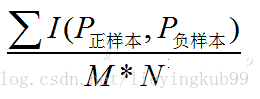
举个例子：

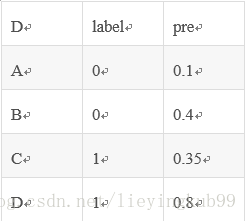
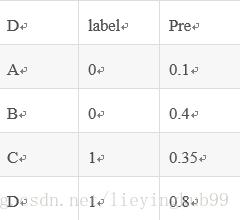
假设有4条样本。2个正样本，2个负样本，那么M*N=4。

即总共有4个样本对。分别是：

（D,B）,（D,A）,(C,B),（C,A）。

在（D,B）样本对中，正样本D预测的概率大于负样本B预测的概率（也就是D的得分比B高），记为1

同理，对于（C,B）。正样本C预测的概率小于负样本C预测的概率，记为0.

那么auc如下：

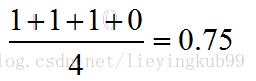
假如出现得分一致的时候：

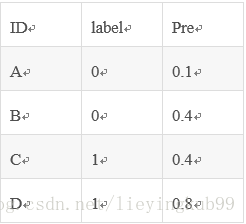
同样本是4个样本对，对于样本对（C,B）其I值为0.5。

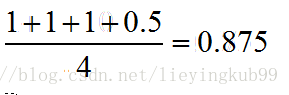
方法二

利公式：

● 对预测概率从高到低排序

● 对每一个概率值设一个rank值（最高的概率的rank为n,第二高的为n-1）

● rank实际上代表了该score（预测概率）超过的样本的数目

为了求的组合中正样本的score值大于负样本，如果所有的正样本score值都是大于负样本的，那么第一位与任意的进行组合score值都要大，我们取它的rank值为n，但是n-1中有M-1是正样例和正样例的组合这种是不在统计范围内的（为计算方便我们取n组，相应的不符合的有M个），所以要减掉，那么同理排在第二位的n-1，会有M-1个是不满足的，依次类推，故得到后面的公式M*(M+1)/2，我们可以验证在正样本score都大于负样本的假设下，AUC的值为1

● 除以M*N

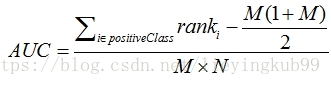
举例说明：

排序。按概率排序后得到：

按照上面的公式，只把正样本的序号加起来也就是只把样本C,D的rank值加起来后减去一个常数项：

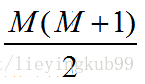
得到：

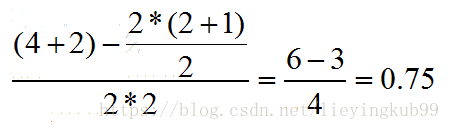
如果出现得分一样的情况：

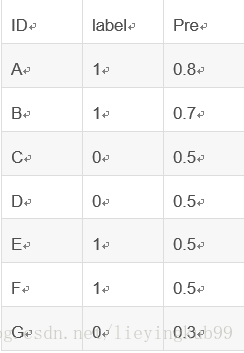
假如有4个取值概率为0.5，而且既有正样本也有负样本的情况。计算的时候，其实原则就是相等得分的rank取平均值。具体来说如下：

先排序：

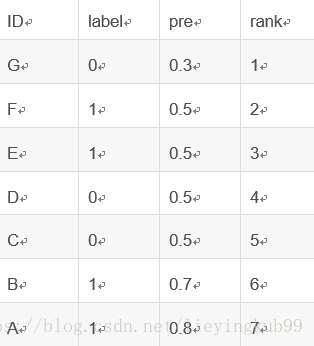
这里需要注意的是：相等概率得分的样本，无论正负，谁在前，谁在后无所谓。

由于只考虑正样本的rank值：

对于正样本A，其rank值为7

对于正样本B，其rank值为6

对于正样本E，其rank值为（5+4+3+2）/4

对于正样本F，其rank值为（5+4+3+2）/4

实现及验证

采用sklearn中的库函数验证：

import numpy as np
from sklearn.metrics import roc_curve
from sklearn.metrics import auc

#---自己按照公式实现
def auc_calculate(labels,preds,n_bins=100):
    postive_len = sum(labels)
    negative_len = len(labels) - postive_len
    total_case = postive_len * negative_len
    pos_histogram = [0 for _ in range(n_bins)]
    neg_histogram = [0 for _ in range(n_bins)]
    bin_width = 1.0 / n_bins
    for i in range(len(labels)):
        nth_bin = int(preds[i]/bin_width)
        if labels[i]==1:
            pos_histogram[nth_bin] += 1
        else:
            neg_histogram[nth_bin] += 1
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(n_bins):
        satisfied_pair += (pos_histogram[i]*accumulated_neg + pos_histogram[i]*neg_histogram[i]*0.5)
        accumulated_neg += neg_histogram[i]

    return satisfied_pair / float(total_case)

if __name__ == '__main__':

    y = np.array([1,0,0,0,1,0,1,0,])
    pred = np.array([0.9, 0.8, 0.3, 0.1,0.4,0.9,0.66,0.7])


    fpr, tpr, thresholds = roc_curve(y, pred, pos_label=1)
    print("-----sklearn:",auc(fpr, tpr))
    print("-----py脚本:",auc_calculate(y,pred))

AUC的优点：

它不受类别不平衡问题的影响，不同的样本比例不会影响AUC的评测结果。在训练时，可以直接使用AUC作为损失函数。