Python计算AUC
strive_1106 人气:0介绍
AUC(Area Under Curve)被定义为ROC曲线下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
auc计算方式:参考Python实现计算AUC的示例代码
实现代码
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = [1,1,0,0,1,1,0]
y_pred = [0.8,0.7,0.5,0.5,0.5,0.5,0.3]
print(roc_auc_score(y_true, y_pred))
# 下面实现的是方法1
# https://blog.csdn.net/lieyingkub99/article/details/81266664?utm_medium=distribute.pc_relevant.none-task-blog-title-1&spm=1001.2101.3001.4242
def cal_auc1(y_true, y_pred):
n_bins = 10
postive_len = sum(y_true) # M正样本个数
negative_len = len(y_true) - postive_len # N负样本个数
total_case = postive_len * negative_len # M * N样本对数
pos_histogram = [0 for _ in range(n_bins)] # 保存每一个概率值下的正样本个数
neg_histogram = [0 for _ in range(n_bins)] # 保存每一个概率值下的负样本个数
bin_width = 1.0 / n_bins
for i in range(len(y_true)):
nth_bin = int(y_pred[i] / bin_width) # 概率值转化为整数下标
if y_true[i] == 1:
pos_histogram[nth_bin] += 1
else:
neg_histogram[nth_bin] += 1
print(pos_histogram)
print(neg_histogram)
accumulated_neg = 0
satisfied_pair = 0
for i in range(n_bins):
satisfied_pair += (pos_histogram[i] * accumulated_neg + pos_histogram[i] * neg_histogram[i] * 0.5)
print(pos_histogram[i], neg_histogram[i], accumulated_neg, satisfied_pair)
accumulated_neg += neg_histogram[i]
return satisfied_pair / float(total_case)
print(cal_auc1(y_true, y_pred))
# 下面实现的是方法2
# https://blog.csdn.net/lieyingkub99/article/details/81266664?utm_medium=distribute.pc_relevant.none-task-blog-title-1&spm=1001.2101.3001.4242
def cal_auc2(y_true, y_pred):
n_bins = 10
postive_len = sum(y_true) # M正样本个数
negative_len = len(y_true) - postive_len # N负样本个数
total_case = postive_len * negative_len # M * N样本对数
prob_rank = [0 for _ in range(n_bins)] # 保存每一个概率值的rank
prob_num = [0 for _ in range(n_bins)] # 保存每一个概率值出现的次数
bin_width = 1.0 / n_bins
raw_arr = []
for i in range(len(y_true)):
raw_arr.append([y_pred[i], y_true[i]])
arr = sorted(raw_arr, key=lambda d: d[0]) # 按概率由低到高排序
for i in range(len(arr)):
nth_bin = int(arr[i][0] / bin_width) # 概率值转化为整数下标
prob_rank[nth_bin] = prob_rank[nth_bin] + i + 1
prob_num[nth_bin] = prob_num[nth_bin] + 1
satisfied_pair = 0
for i in range(len(arr)):
if arr[i][1] == 1:
nth_bin = int(arr[i][0] / bin_width) # 概率值转化为整数下标
satisfied_pair = satisfied_pair + prob_rank[nth_bin] / prob_num[nth_bin]
return (satisfied_pair - postive_len * (postive_len + 1) / 2 ) / total_case
print(cal_auc2(y_true, y_pred))
# 根据roc曲线,找不同点算下面积, 需要点足够多
def cal_auc3(y_true, y_pred):
"""Summary
Args:
raw_arr (TYPE): Description
Returns:
TYPE: Description
"""
raw_arr = []
for i in range(len(y_true)):
raw_arr.append([y_pred[i], y_true[i]])
print(raw_arr)
arr = sorted(raw_arr, key=lambda d:d[0], reverse=True)
pos, neg = 0., 0.
for record in arr:
if record[1] == 1.:
pos += 1
else:
neg += 1
fp, tp = 0., 0.
xy_arr = []
for record in arr:
if record[1] == 1.:
tp += 1
else:
fp += 1
xy_arr.append([fp/neg, tp/pos])
print(xy_arr)
auc = 0.
prev_x = 0.
prev_y = 0.
for x, y in xy_arr:
if x != prev_x:
auc += ((x - prev_x) * (y + prev_y) / 2.)
prev_x = x
prev_y = y
print(auc)
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = [1, 1, 0, 0, 1, 1, 0]
y_pred = [0.8, 0.7, 0.5, 0.5, 0.5, 0.5, 0.3]
print(roc_auc_score(y_true, y_pred))方法补充
下面是小编为大家找到的另外三个计算AUC的代码,会输出三种方法各自的auc,以及通过面积计算AUC时的ROC曲线。
在通过面积计算AUC的方法中,没有遍历数据的预测概率作为分类阈值,而是对[0,1]区间等分得到一系列阈值。
# AUC的计算
import numpy as np
import matplotlib.pyplot as plt
for e in range(3):
print("\nRound: ", e+1)
num = 1000
auc1 = auc2 = auc3 = 0.
# 准备数据
pred_prob = list(np.random.uniform(low=0,high=1, size=[num]))
labels = [int(prob>0.5) for prob in list(np.random.uniform(low=0,high=1, size=[num]))]
# 检查数据
# print("pred_prob:\n", pred_prob)
# print("labels:\n", labels)
# 方法一,面积加和
roc_point = []
for i in range(num):
i = pred_prob[i]
TP = 0 # 真阳样本数
FP = 0 # 假阳样本数
TP_rate = 0. # 真阳率
FP_rate = 0. # 假阳率
pos_num = 0 # 预测真样本数
# 计数过程
for ind, prob in enumerate(pred_prob):
if prob>i:
pos_num += 1
if prob>i and labels[ind]>0.5:
TP+=1
elif prob>i and labels[ind]<0.5:
FP+=1
if pos_num!=0:
TP_rate = TP / sum(labels)
FP_rate = FP / (num-sum(labels))
roc_point.append([FP_rate, TP_rate]) # 记录ROC中的点
# 画出ROC曲线
roc_point.sort(key=lambda x: x[0])
plt.plot(np.array(roc_point)[1:, 0], np.array(roc_point)[1: ,1])
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.show()
# 计算每个小长方形的面积,求和即为auc
lastx = 0.
for x,y in roc_point:
auc1 += (x-lastx)*y # 底乘高
lastx = x
print("方法一 auc:", auc1)
# 方法二,利用AUC关于排列概率的定义计算
auc2 = 0
P_ind = [] # 正样本下标
F_ind = [] # 负样本下标
P_F = 0 # 正样本分数高于负样本的数量
F_P = 0 # 负样本分数高于正样本的数量
# 计数过程
for ind, val in enumerate(labels):
if val > 0.5:
P_ind.append(ind)
else:
F_ind.append(ind)
for Pi in P_ind:
for Fi in F_ind:
if pred_prob[Pi] > pred_prob[Fi]:
P_F += 1
else:
F_P += 1
auc2 = P_F/(len(P_ind)*len(F_ind))
print("方法二 auc:", auc2)
# 方法三,方法二的改进,简化了计算,降低了时间复杂度
new_data = [[p, l] for p, l in zip(pred_prob, labels)]
new_data.sort(key=lambda x:x[0])
# 求正样本rank之和
rank_sum = 0
for ind, [prob,label] in enumerate(new_data):
if label>0.5:
rank_sum+=ind
auc3 = (rank_sum - len(P_ind)*(1+len(P_ind))/2) / (len(P_ind)*len(F_ind))
print("方法三 auc:", auc3)运行结果

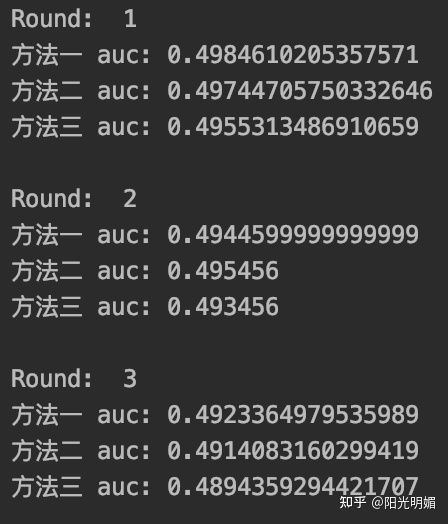
加载全部内容