C++组合数的计算
一起摸摸鱼 人气:0组合数的计算
使用加法递推—O(n^2)

边界条件
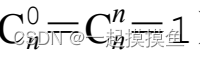
int C[1001][1001]; // 根据实际需要开数组,必要时采用高精度类型
//……
memset(C,0,sizeof(C));
for (int i=0;i<=n;i++)
{
C[i][0]=1;
for (int j=0;j<=i;j++)
C[i][j]=C[i-1][j-1] + C[i-1][j];
}使用乘法递推—O(n)
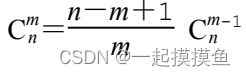
边界条件

必须先乘后除,否则除不开
一个小优化:
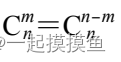
(m>n/2时用)
int C[1001]; // C[m]其实表示C[n][m],必要时采用高精度类型 …… C[0]=1; if (m>n-m) m=n-m; for (int i=1;i<=m;i++) C[i] = (n-i+1) * C[i-1] / i; // 如果怕溢出,可以把中间结果转化成long long。
排列和组合的产生(无重集元素)
int item[N]; // 第i位要放置的数字 bool used[N]; int n,m;
全排列
将 n 个数字 1~n 进行排序,有多少种排序方法?
使用深度优先搜索,对 n 个位置逐个进行试探。时间复杂度为 O(n!)。
void full_ permutation(int depth)
{
if (depth==n)
{
// print(); // 输出结果
return;
}
for (int i=0; i<n; i++)
if (!used[i])
{
used[i]=true;
item[depth]=i+1;
try(depth+1);
used[i]=false; // 别忘记清除”使用”标记
}
}一般组合
从 n 个元素 1~n 中任取 m 个元素,有多少种取法?
一个合法的组合有这样一个特点:排在右面的数字一定严格大于左面的数字。比如说某一位上取了 3,那么从 4 开始搜索下一位就可以了。
void combination(int depth, int p)
{
if (depth==m)
{
// print(); // 输出结果
return;
}
for (int i=p+1 ; i<n-(m-depth) ; i++)
{
// 由于后面的元素一定前面的大,所以不需要标记used了。
item[depth]=i;
try(depth+1);
}
}
combination(0,0);全组合
输入 n 个数,求这 n 个数构成的集合的所有非空子集。
和一般组合不同,这次只要产生一个解,就马上输出。
void full_combination(int l, int p)
{
for (int i=0; i<l; i++) // 每次进入递归函数都输出
cout<<item[i]<<" ";
cout<<endl;
for (int i=p; i<n; i++)
{
item[l] = i; // 在l位置放上该数
full_combination(l+1, i+1); // 填下一个位置
}
}
full_combination(0, 0); 注意:对于一个整数,每一位不是 0 就是 1,所以可以用整数来表示一个集合。具体实例可参见 “2.8Healthy Holsteins”。
由上一排列产生下一排列
① 从右往左寻找第一个小于右边的数,位置为 j。
② 在 j 位置的右边寻找大于 aj的最小数字 ak(位置 k)
③ 将 aj 与 ak的值进行交换
④ 将数列的 j+1 位到 n 位倒转。
int a[N]; // 初始化:a[i]是字典序最小的排列, 0≤i<N
int j,k, p,q, temp;
j=(n-1) - 1;
while ((j>=0)&&(a[j]>a[j+1])) j--; // 从右往左寻找第一个小于右边的数,位置为j。
if (j>=0) // 如果j<0说明已经排完了。
{
k=n-1;
while (a[k]<a[j]) k--; // 在j位置的右边寻找大于aj的最小数字ak(位置k)
swap(a[j], a[k]); // 将aj与ak的值进行交换
for (p=j+1,q=n-1; p<q; p++,q--) // 将数列的j+1位到n位倒转
swap(a[p], a[q]);
}STL 中有与此相同的算法。头文件为<algorithm>。
next_permutation(序列第一项的地址, 序列最后一项的地址+1):产生下一排列。
prev_permutation(序列第一项的地址, 序列最后一项的地址+1):产生上一排列。
这两个函数能够用于可重集的排列。
由上一组合产生下一组合
① 从右向左寻找可以往下取一个元素的数,位置为 j。
(举个例子:从 7 个数中取 4 个数,有一个组合为 1367,那么 6、7 就不能再往下取了)
② 数列的 j 位到 n 位重新取元素。
注意:
① 从 N 个连续元素中取 M 个元素。如果元素序号不连续,就需要修改下面的“+1”。
② 右侧的数字一定严格大于左侧的数字。
int a[M]; // 初始化:a[i]是字典序最小的排序, 0≤i<M,1≤a[i]≤N
//……
int j=m-1;
while ((j>=0)&&(a[j]==n-(m-1 -j))) j--;
if (i>=0)
{
a[j]++;
for (int k=j+1; k<m; k++) a[k]=a[k-1]+1;
}加载全部内容