Python control

时间:2022-09-28 荷碧·TongZJ 人气:0

传递函数

创建传递函数有两种方式：

import control as ctrl
 
# 方式 1
s = ctrl.tf('s')
sys = 100 / (s ** 2 + 10 * s + 100)
 
# 方式 2
sys = ctrl.tf([100], [1, 10, 100])

对 tf 这个类，它内置的方法可求解零点、极点、特征参数、特征根

# 求零点
sys.zero()
 
# 求极点
sys.pole()
 
# 特征参数、特征根
sys.damp()

输入响应

# 阶跃动态指标
step_info(sys)
# 阶跃响应
t, response = step_response(sys, T)
 
# 脉冲响应
t, response = impulse_response(sys, T)
 
t, response = initial_response(sys, T)
t, response = forced_response(sys, T)

T 是响应的时间，可以是 float (即时间上限)，也可以是数组

阶跃动态指标是 dict 类型，包括：'RiseTime', 'SettlingTime', 'SettlingMin', 'SettlingMax', 'Overshoot', 'Undershoot', 'Peak', 'PeakTime', 'SteadyStateValue'

系统绘图

# Nyquist图, 可传入列表
nyquist_plot(sys)
 
# Bode图, 可传入列表
bode_plot(sys)
 
# 根轨迹图
root_locus(sys)

绘图使用的是 matplotlib.pyplot，所以执行完函数后，要加上 plt.show() 才会显示图像

Laplace 逆变换

可能是我太弱找不到这个包的 Laplace 逆变换函数，也可能是这个包真的没有这个函数

于是我利用 sympy 这个包求解：定义时域响应这个类，__call__ 使其可以计算时间数组 (np.array) 的响应

import sympy
class Time_Response:
    ''' 时域响应'''
    s, t = sympy.symbols('s, t')
 
    def __init__(self, fun, doprint=False):
        ''' fun: 返回关于s的传递函数的 function
            doprint: 输出公式'''
        sys = fun(self.s)
        self.f_t = sympy.integrals.inverse_laplace_transform(sys, s=self.s, t=self.t)
        if doprint:
            sympy.pprint(self.f_t)
 
    def __call__(self, time):
        ''' 使自身可作为函数被调用'''
        response = list(map(lambda i: float(self.f_t.subs({self.t: i})), time))
        return np.array(response)

设置 doprint 为 True，则可以输出时域响应的方程 —— 但是问题在于，自动控制原理里面的 Laplace 变换是默认 F(s) 各阶导数的初始值均为 0 的，这个条件我没有办法加入到 sympy 的求解过程里，所以结果看起来就有些奇怪

import control as ctrl
import matplotlib.pyplot as plt
import numpy as np
 
# 自定义类所在的模块
from mod.math_model import Time_Response
orange = 'orange'
blue = 'deepskyblue'
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
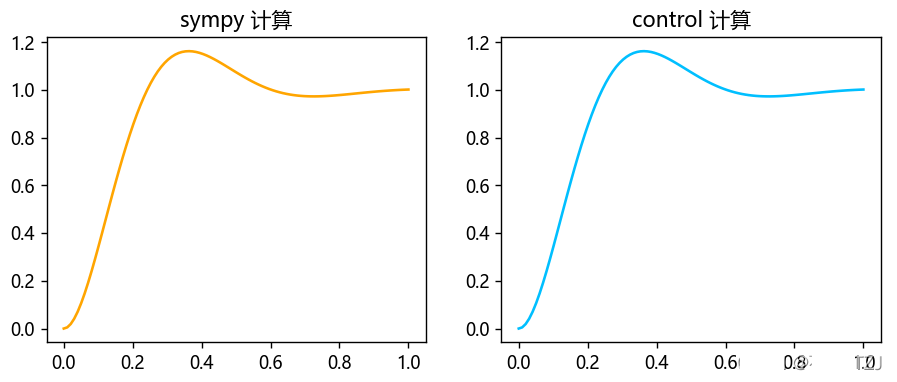
f_t = Time_Response(lambda s: 100 / (s ** 2 + 10 * s + 100) / s, doprint=True)
t = np.linspace(0, 1, 100)
plt.subplot(1, 2, 1)
plt.title('sympy 计算')
plt.plot(t, f_t(t), c=orange)
s = ctrl.tf('s')
sys = 100 / (s ** 2 + 10 * s + 100)
t, response = ctrl.step_response(sys, T=1)
plt.subplot(1, 2, 2)
plt.title('control 计算')
plt.plot(t, response, c=blue)
plt.show()

对比 sympy 和 control 求解的响应曲线：一毛一样

加载全部内容