C++拓扑排序

时间:2022-09-28 菠菠萝宝人气:1

前言

在软件开发、施工过程、教学安排等等的一系列活动中，往往需要一个有向无环图来表示其是否成成功进行下去。

在一个有向图为顶点表示活动的网中，我们称为AOV网（Activity On Vertex Network）。设G={V,E}是一个具有n个顶点的有向图，V中的顶点序列v1,v2,…,vn,满足若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在vj之前。则我们称这样的顶点为一个拓扑序列。

所谓拓扑排序，其实就是对一个有向图构造拓扑序列的过程。如果所有的顶点被输出，则说明有向图中不存在回路，反之则是有回路。

一、拓扑排序算法的思路

拓扑排序往往用在有向邻接表中，这里也就只用有向邻接表来实现。

先找出所有节点的入度。

再在AOV网中选择一个入度为0的顶点输出，然后删除此顶点，将其连接的节点的入度减一直至输出所有顶点或者AOV网中不存在入度为0的顶点为止。

二、实现步骤

1.求个顶点的入度

设置一个indegree数组来存放各个顶点的入度。

int* indegree = (int*)malloc(sizeof(int) * G.vexnum);
//对单个节点p求入度
void CountIndegree(AdjList g, int* indegree, ArcNode* p) {
	while (p != NULL) {
		indegree[p->adjvex]++;
		p = p->nextarc;
	}
	return;
}

2.拓扑排序的实现

这里对栈的使用还是调用stl中的stack，比较方便。

bool TopoSort(AdjList g, int* indegree) {
	//先清空申请的indegree数组，或者也可以在初始化时采用calloc，就不用在这里置为0了
	for (int i = 0; i < g.vexnum; i++) {
		indegree[i] = 0;
	}
	//遍历边表中的每一个顶点，用CountIndegree()遍历单个节点
	for (int i = 0; i < g.vexnum; i++) {
		ArcNode* p = g.vertexlist[i].firstarc;
		CountIndegree(g, indegree, p);
	}
	stack<int>S;
	//如果该顶点的入度为0，则入栈。
	for (int i = 0; i < g.vexnum; i++) {
		if (indegree[i] == 0) {
			S.push(i);
		}
	}
	//count用来表示已经输出的节点个数
	//如果所有的顶点被输出，则count==g.vexnum，无回路，反之count<g.vexnum,则是有回路。
	int count = 0;
	while (!S.empty()) {
		int top = S.top();
		printf("%c ", g.vertexlist[top].data);
		S.pop();
		count++;
		ArcNode* p = g.vertexlist[top].firstarc;
		for (p; p != NULL; p = p->nextarc) {
			int i = p->adjvex;
			if (--indegree[i] == 0) {
				S.push(i);
			}
		}
	}
	if (count == g.vexnum) {
		return true;
	}
	return false;
}

三、测试结果

自己花了一个看起来挺复杂的图，一下也看不出来有没有环

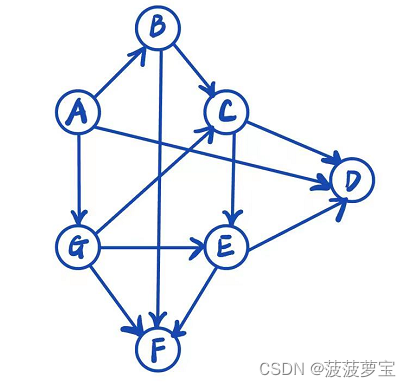
首先算一算入度，顺带打印一下。

接下来是拓扑排序的结果

完美！

总结

每个顶点进栈一次出战一次，度减一的操作执行了e次，所以整个算法的时间复杂度为O(n+e)。

加载全部内容