Java排序
菜菜不恰菜 人气:0稳定性
两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法。
直接插入排序
直接插入排序就是每次选择无序区间的第一个元素,在有序区间内选择合适的位置插入。
从数组下标为1开始,将下标为1上的值取出来放在tmp中,然后它和前面的下标j上的值进行比较,如果前面下标j上的值比它大,则前面下标j上的值往后走一步,直到比到j回退到了-1或者j下标上的值比tmp小为止,然后把tmp插入到下标为[j+1]的位置上。然后i就继续往后走,继续比较,直到i走到数组的最后。
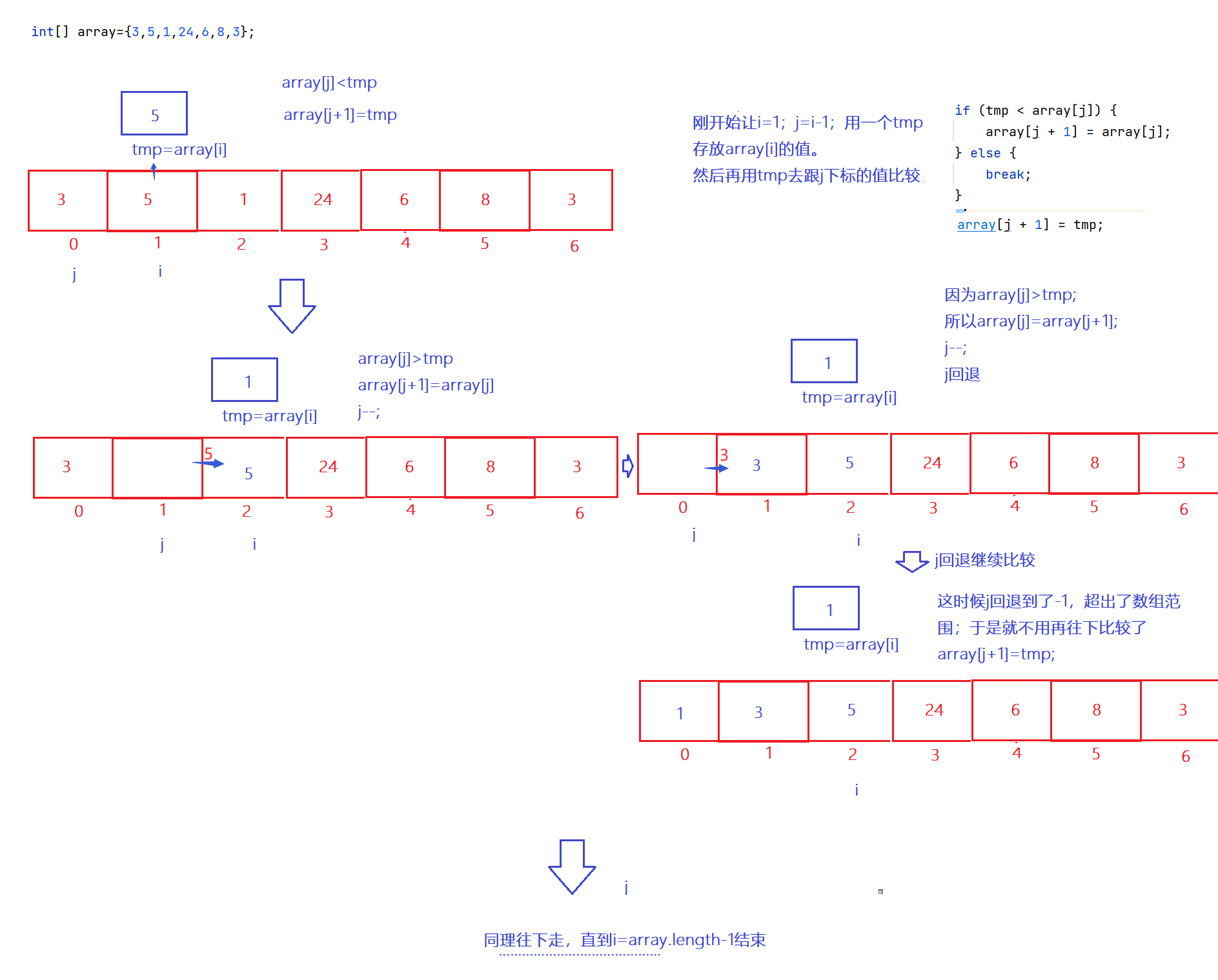
代码示例:
/**
*直接插入排序
*时间复杂度 O(N^2)
*空间复杂度 O(1)
*稳定性 :稳定(看在比较的过程当中是否发生了跳跃式的交换,如果发生了跳跃式的交换那么就是不稳定的排序)
* 一个稳定的排序,可以实现为不稳定的排序
* 但是一个本身就不稳定的排序,是不可以变成稳定的排序的
* 经常使用在数据量不多且整体数据趋于有序了
*/
public static void insertSort(int[] array) {
for(int i=1;i<array.length;i++) {
int tmp = array[i];
int j = 0;
for (j = i - 1; j >= 0; j--) {
if (tmp < array[j]) {
array[j + 1] = array[j];
} else {
break;
}
}
array[j + 1] = tmp;
}
}希尔排序
希尔排序是对直接插入排序的优化。将数据进行相应的分组,分为gap组,然后按照直接插入排序的方法排序。 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
/**
* 时间复杂度(和增量有关系的):O(n^1.3 - n^1.5)
* 空间复杂度:O(1)
* 稳定性:不稳定的
* 看在比较的过程当中是否发生了跳跃式的交换,如果发生了跳跃式的交换那么就是不稳定的排序
*/
public static void shellSort(int[] array) {
int gap=array.length-1;
while(gap>1){
shell(array,gap);
gap/=2;
}
shell(array,1);//保证最后是1组
}
public static void shell(int[] array,int gap) {
for(int i=gap;i< array.length;i++){
int tmp=array[i];
int j=i-gap;
for (j = i-gap; j >=0; j=j-gap) {
if(tmp<array[j]){
array[j+gap]=array[j];
}else{
break;
}
}
array[j+gap]=tmp;
}
}选择排序
每一次从无序区间选出最大(或最小)的一个元素,存放在无序区间的最后(或最前),直到全部待排序的数据元素排完 。
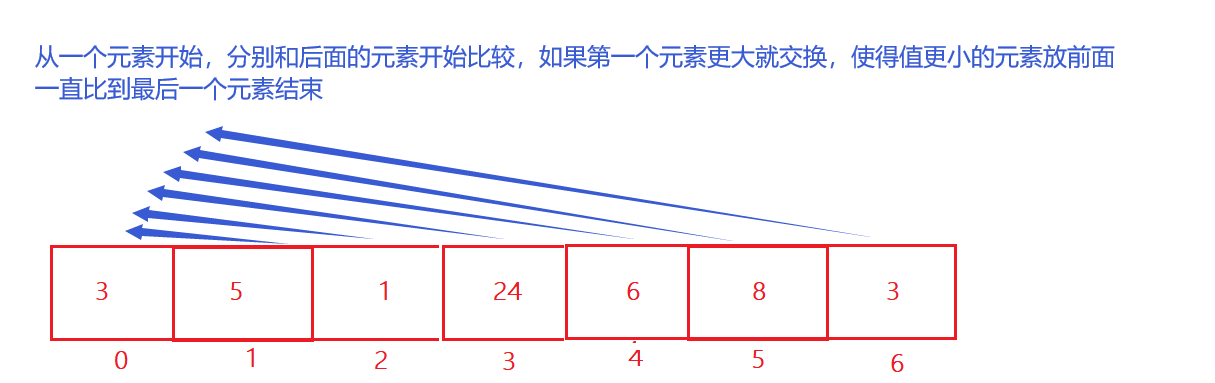
代码示例:
/**
*选择排序
*空间复杂度:O(N^2)
* 时间复杂度:O(1)
* 稳定性:不稳定
* 看在比较的过程当中是否发生了跳跃式的交换,如果发生了跳跃式的交换那么就是不稳定的排序
*/
public static void selectSort(int[] array){
for(int i=0;i<array.length;i++){
for(int j=i+1;j< array.length;j++){
if(array[j]<array[i]){
swap(array,i,j);
}
}
}
}
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
//选择排序还可以找到最小值下标再交换
public static void selectSort1(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i+1; j < array.length; j++) {
//找到最小值下标
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,i,minIndex);
}堆排序
基本原理也是选择排序,只是不在使用遍历的方式查找无序区间的最大的数,而是通过堆来选择无序区间的最大的数。
注意: 排升序要建大堆;排降序要建小堆。 (在堆那里有提过)
代码示例:
/**
* 堆排序
* 时间复杂度:O(N*log2^N)
* 空间复杂度:O(1)
* 稳定性:不稳定
*/
public static void heapSort(int[] array){
creatHeap(array);//先创建堆
int end=array.length-1;
//交换后调整(N*log2^N)
while(end>0){
swap(array,0,end);
shiftDown(array,0,end);
end--;
}
}
//建堆
public static void creatHeap(int[] array){
for(int parent=(array.length-1-1)/2;parent>=0;parent--){
shiftDown(array,parent,array.length);
}
}
//调整
public static void shiftDown(int[] array,int parent,int len){
int child=2*parent+1;//左孩子下标
while(child<len){
//左右孩子比较
if(child+1<len && array[child]<array[child+1]){
child++;
}
if(array[child]>array[parent]){
swap(array,child,parent);
parent=child;
child=parent*2-1;
}else{
break;
}
}
}冒泡排序
在无序区间,通过相邻数的比较,将最大的数冒泡到无序区间的最后,持续这个过程,直到数组整体有序。

代码示例:
/**
* 冒泡排序
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:稳定
* i为需要排的次数
* j为每次需要比较的开始到结束位置
*/
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-1-i; j++) {
if(array[j+1]<array[j]){
swap(array,j,j+1);
}
}
}
}
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}快速排序
1、 从待排序区间选择一个数,作为基准值 (pivot) ;
2、 partition: 遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等的)放到基准值的右边;
3、 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度 == 1 ,代表已经有序,或者小区间的长度 == 0 ,代表没有数据。 代码示例:
/**
* 时间复杂度:
* 最好(每次可以均匀的分割待排序序列):O(N*log2^n)log以2为底的N次方
* 最坏:数据有序或者逆序的情况 O(N^2)
* 空间复杂度:
* 最好:O(log2^n)
* 最坏:O(n) 单分支的一棵树
* 稳定性:不稳定的排序
*/
//递归方式实现
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
public static void quick(int[] array,int left,int right){
if(left>=right){
return;
}
//找基准值,然后基准值左边右边分别按同样的方式处理
int pivot=partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
//找基准点(两边开始找)
public static int partition(int[] array,int start,int end){
int tmp=array[start];
while(start<end){
while(start<end && array[end]>=tmp){
end--;
}
array[start]=array[end];
while(start<end && array[start]<=tmp){
start++;
}
array[end]=array[start];
}
array[start]=tmp;//start==end时,找到了基准点
return end;
}上面代码还有待优化,如果我们是一个有序数组,我们在找基准值进行相应处理的时候可能会出现单分支情况,这时候我们可以让start下标的值为中间值,这样可以避免出现单分支情况。
代码示例:
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
public static void quick(int[] array,int left,int right){
if(left>=right){
return;
}
//优化--找基准前,先找到中间值,三数取中法(防止有序情况下出现单分支)
int minValIndex=findValINdex(array,left,right);
swap(array,minValIndex,left);
int pivot=partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
//三数取中
private static int findValINdex(int[] array,int start,int end){
int mid=start+((end-start)>>>1);
//(start+end)/2
if(array[start]<array[end]){
if(array[mid]>array[end]){
return end;
} else if (array[mid]<array[start]) {
return start;
}else{
return mid;
}
}else{
if(array[mid]>array[start]) {
return start;
}else if(array[mid]<array[end]){
return end;
}else{
return mid;
}
}
}当排序数据过多时还能继续优化,如果区间内的数据,在排序的过程当中,小于某个范围了,可以使用直接插入排序。
代码示例:
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
//递归,找到了基准点,分别再对基准点左边和基准点右边找
public static void quick(int[] array,int left,int right){
if(left>=right){
return;
}
//优化--如果区间内的数据,在排序的过程当中,小于某个范围了,可以使用直接插入排序
if(right-left+1<150){
insertSort1(array,left,right);
return;
}
//优化--找基准前,先找到中间值,三数取中法(防止有序情况下出现单分支)
int minValIndex=findValINdex(array,left,right);
swap(array,minValIndex,left);
int pivot=partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
private static void insertSort1(int[] array,int start,int end){
for (int i = 1; i <= end; i++) {
int tmp=array[i];
int j=i-1;
for(j=i-1;j>=start;j--){
if(array[j]>tmp){
array[j+1]=array[j];
}else{
//array[j+1]=tmp;
break;
}
}
array[j+1]=tmp;
}
}非递归实现:
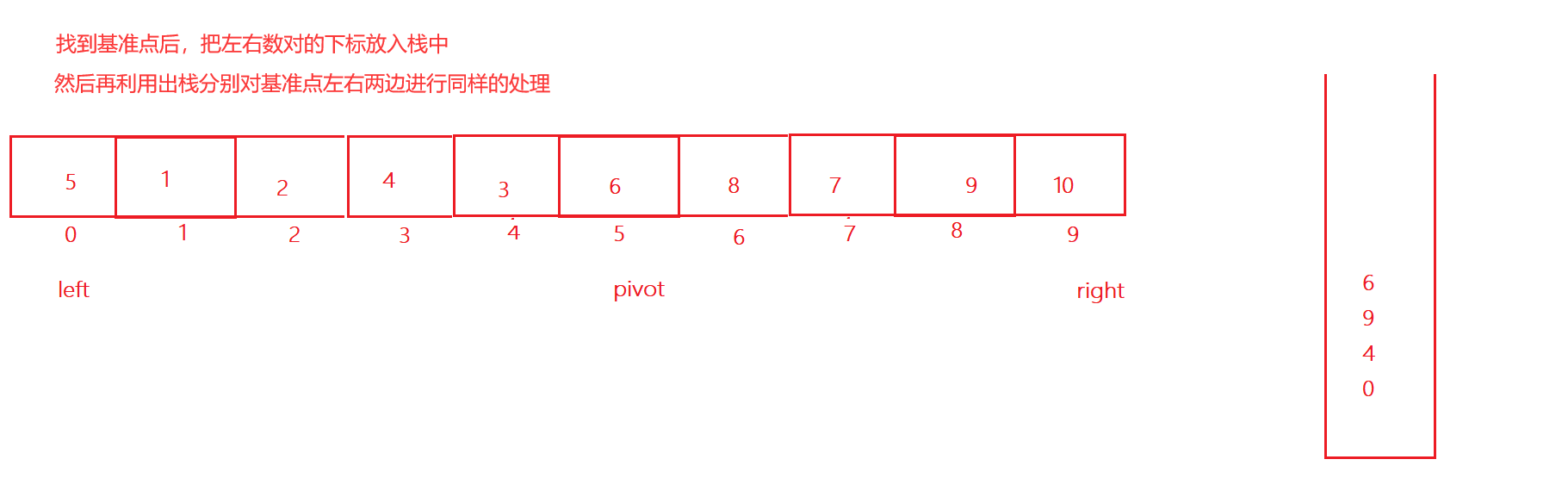
public static void quickSort1(int[] array){
int left=0;
int right=array.length-1;
Stack<Integer> stack=new Stack<>();
int pivot=partition(array,left,right);
//如果左边或者右边只剩下一个数据了,那就已经有序了,不需要在排序
if(left+1<pivot){
//左边至少有两个元素
stack.push(left);
stack.push(pivot-1);
}
if(right-1>pivot){
//右边至少有两个元素
stack.push(right);
stack.push(pivot+1);
}
while(!stack.isEmpty()){
left=stack.pop();
right=stack.pop();
pivot=partition(array,left,right);
if(left+1<pivot){
//左边至少有两个元素
stack.push(left);
stack.push(pivot-1);
}
if(right-1>pivot){
//右边至少有两个元素
stack.push(right);
stack.push(pivot+1);
}
}
}归并排序
归并排序 是建立在归并操作上的一种有效的排序算法 , 将已有序的子序列合并,得到完全有序的序列。即先使每个子序列有序,再使子 序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。

代码示例:
/**
* 归并排序--递归
* 时间复杂度:O(N*log2^N)
* 空间复杂度:O(N)
* 稳定性:稳定
* 学过的排序:稳定的只有三个
* 冒泡 插入 归并
*/
//递归方式实现
public static void mergeSort(int[] array){
mergeSortInternal(array,0,array.length-1);
}
public static void mergeSortInternal(int[] array,int left,int right){
if(left>=right){
return;
}
int mid=left+((right-left)>>>1);
//mid=(left+right)/2;
//左边
mergeSortInternal(array,left,mid);
//右边
mergeSortInternal(array,mid+1,right);
//合并
merge(array,left,mid,right);
}
public static void merge(int[] array,int start,int mid,int end) {
int s1 = start;
int e1 = mid;
int s2 = mid+1;
int e2 = end;
int i = 0;
int[] tmp = new int[array.length];
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <=array[s2]) {
tmp[i] = array[s1];
//tmp[i++]=array1[s1++];
i++;
s1++;
} else {
tmp[i] = array[s2];
i++;
s2++;
}
}
while(s1<=e1){
tmp[i++]=array[s1++];
}
while(s2<=e2){
tmp[i++]=array[s2++];
}
for (int j = 0; j < i; j++) {
array[j+start]=tmp[j];
}
}非递归方式--分组归并(先tmp个元素有序然后在合并)
//tmp:代表组内元素个数
public static void mergeSort1(int[] array){
int tmp=1;
while(tmp<array.length-1){
//数组每次都要进行遍历,确定要归并的区间
for (int i = 0; i < array.length; i+=tmp*2) {
int left=i;
int mid=left+tmp-1;
//防止越界
if(mid>=array.length){
mid=array.length-1;
}
int right=mid+tmp;
//防止越界
if(right>=array.length){
right=array.length-1;
}
//下标确定之后进行合并
merge(array,left,mid,right);
}
tmp=tmp*2;
}
}计数排序
以上排序都是通过比较的排序,接下来介绍一种不需要比较的排序--计数排序。
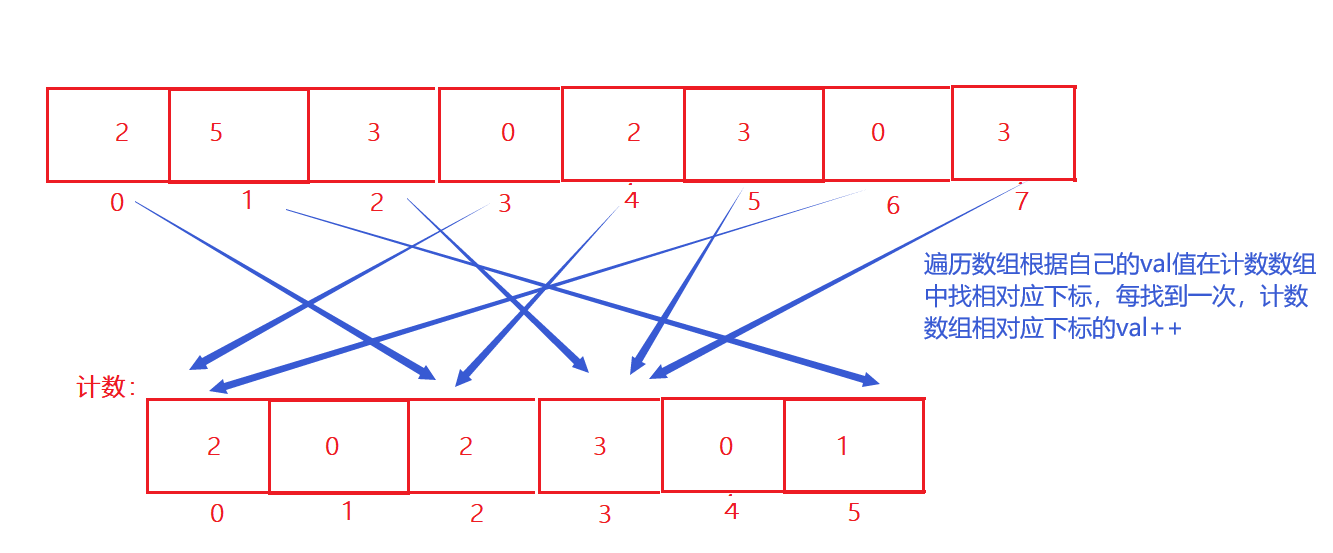
代码示例:
/**
* 计数排序:
* 时间复杂度:O(N)
* 空间复杂度:O(M) M:代表当前数据的范围
* 稳定性:当前代码是不稳定的,但是本质是稳定的
* 一般适用于有n个数,数据范围是0-n之间的
*/
public static void countingSort(int[] array) {
int minVal=array[0];
int maxVal=array[0];
for(int i=0;i<array.length;i++){
if(array[i]<minVal){
minVal=array[i];
}
if(array[i]>maxVal){
maxVal=array[i];
}
}
int[] count=new int[maxVal-minVal+1];//下标默认从0开始
for (int i=0;i<array.length;i++){
//统计array数组当中,每个数据出现的次数
int index=array[i];
//为了空间的合理使用 这里需要index-minVal 防止623-600
count[index-minVal]++;
}
//说明,在计数数组当中,已经把array数组当中,每个数据出现的次数已经统计好了
//接下来,只需要,遍历计数数组,把数据写回array
int indexArray=0;
for(int i=0;i<count.length;i++){
while (count[i]>0){
array[indexArray]=i+minVal;
count[i]--;
indexArray++;
}
}
}加载全部内容