Python numpy.transpose
November丶Chopin 人气:0前言
看Python代码时,碰见 numpy.transpose 用于高维数组时挺让人费解,通过一番画图分析和代码验证,发现 transpose 用法还是很简单的。
注:评论中说的三维坐标图中的 0 1 2 3 标反了,已经修正,感谢大家提醒(2019.02)。
正文
Numpy 文档 numpy.transpose 中做了些解释,transpose 作用是改变序列,下面是一些文档Examples:
代码1:
x = np.arange(4).reshape((2,2))
输出1:
#x 为:
array([[0, 1],
[2, 3]])
代码2:
import numpy as np x.transpose()
输出2:
array([[0, 2],
[1, 3]])
对于二维 ndarray,transpose在不指定参数是默认是矩阵转置。如果指定参数,有如下相应结果:
代码3:
x.transpose((0,1))
输出3:
# x 没有变化
array([[0, 1],
[2, 3]])
代码4:
x.transpose((1,0))
输出4:
# x 转置了
array([[0, 2],
[1, 3]])
这个很好理解:
对于x,因为:
代码5:
x[0][0] == 0 x[0][1] == 1 x[1][0] == 2 x[1][1] == 3
我们不妨设第一个方括号“[]”为 0轴 ,第二个方括号为 1轴 ,则x可在 0-1坐标系 下表示如下:
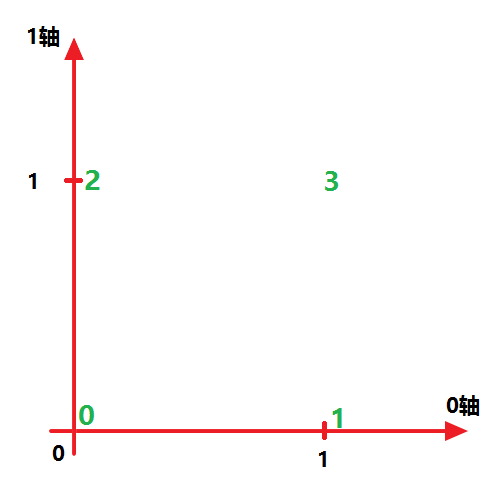
代码6:
因为 x.transpose((0,1)) 表示按照原坐标轴改变序列,也就是保持不变
而 x.transpose((1,0)) 表示交换 ‘0轴’ 和 ‘1轴’,所以就得到如下图所示结果:
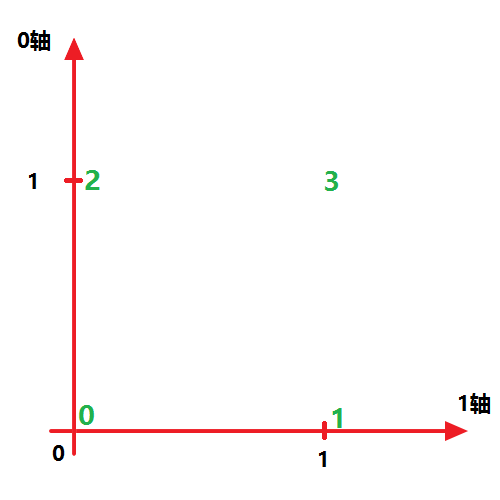
注意,任何时候你都要保持清醒,告诉自己第一个方括号“[]”为 0轴 ,第二个方括号为 1轴
此时,transpose转换关系就清晰了。
我们来看一个三维的:
代码7:
import numpy as np # A是array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]) A = np.arange(16) # 将A变换为三维矩阵 A = A.reshape(2,2,4) print(A)
输出7:
A = array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
我们对上述的A表示成如下三维坐标的形式:
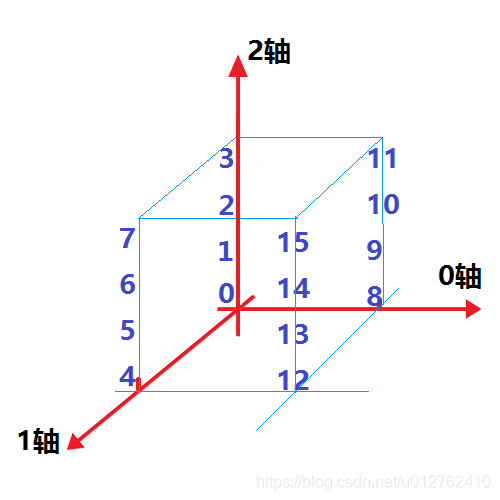
所以对于如下的变换都很好理解啦:
代码8:
A.transpose((0,1,2)) #保持A不变 A.transpose((1,0,2)) #将 0轴 和 1轴 交换
将 0轴 和 1轴 交换:
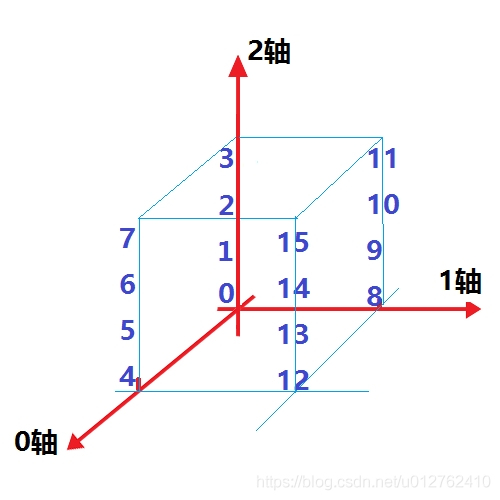
此时,输出
代码9:
A.transpose((1,0,2)) [0][1][2] #根据上图这个结果应该是10
后面不同的参数以此类推。
加载全部内容