Python梯度下降法
侯小啾 人气:01. 读取数据
首先要做的就是读取数据,请自行准备一组适合做多元回归的数据即可。这里以data.csv为例,这里做的是二元回归。导入相关库,及相关代码如下。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data = np.loadtxt("data.csv", delimiter=",")
# 提取特征数据与标签
x_data = data[:,0:-1]
y_data = data[:,-1]
2.定义代价函数
回归模型形如:
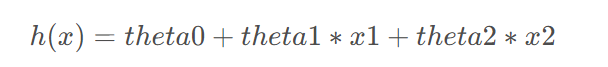
接下来我们需要初始化相关参数,并定义出代价函数。因为存在多个系数参数,这里代价函数的写法与一元回归时的情况略有不同,稍微有所调整。具体如下:
# 初始化一系列参数
# 截距
theta0 = 0
# 系数
theta1 = 0
theta2 = 0
# 学习率
learning_rate = 0.0001
# 初始化迭代次数
n_iterables = 1000
# 定义代价函数(损失函数)
def compute_mse(theta0, theta1, theta2, x_data, y_data):
total_error = 0
for i in range(len(x_data)):
# 计算损失 真实值:y_data 预测值h(x)=theta0 + theta1*x1 + theta2*x2
total_error += (y_data[i] - (theta0 + theta1 * x_data[i, 0] + theta2 * x_data[i, 1])) ** 2
mse_ = total_error / len(x_data) / 2
return mse_
3. 梯度下降
多元回归的梯度下降与一元回归的差不多,在一元回归中只需要求一个导数,而现在求多个偏导数。代码过程如下:
def gradient_descent(x_data, y_data, theta0, theta1, theta2, learning_rate, n_iterables):
m = len(x_data)
# 循环 --> 迭代次数
for i in range(n_iterables):
# 初始化 theta0 theta1 theta2 的偏导值
theta0_grad = 0
theta1_grad = 0
theta2_grad = 0
# 计算偏导的总和再平均
# 遍历m次
for j in range(m):
theta0_grad += (1 / m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
theta1_grad += (1 / m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j]) * x_data[
j, 0]
theta2_grad += (1 / m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j]) * x_data[
j, 1]
# 更新theta
theta0 = theta0 - (learning_rate * theta0_grad)
theta1 = theta1 - (learning_rate * theta1_grad)
theta2 = theta2 - (learning_rate * theta2_grad)
return theta0, theta1, theta2
print(f"开始:截距theta0={theta0},theta1={theta1},theta2={theta2},损失={compute_mse(theta0,theta1,theta2,x_data,y_data)}")
print("开始运行")
theta0,theta1,theta2 = gradient_descent(x_data,y_data,theta0,theta1,theta2,learning_rate,n_iterables)
print(f"迭代{n_iterables}次后:截距theta0={theta0},theta1={theta1},theta2={theta2},损失={compute_mse(theta0,theta1,theta2,x_data,y_data)}")
执行结果输出如下:

1000次迭代之后,损失值由23.64变为0.3865。
4.可视化展示
可视化展示常常作为机器学习过程的补充,可以使得机器学习的效果更为生动,直观。
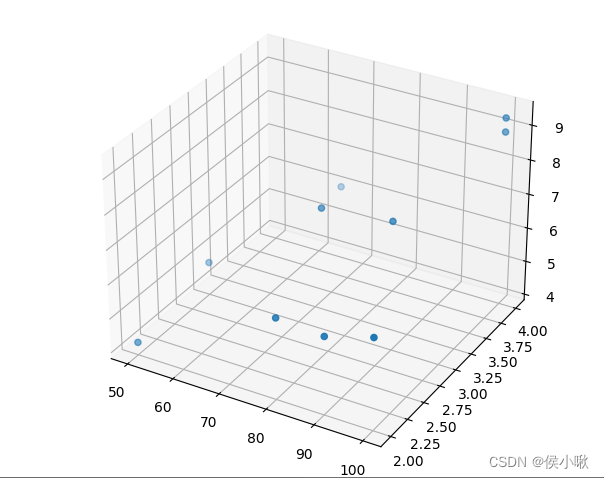
# 可视化散点分布
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x_data[:,0],x_data[:,1],y_data)
plt.show()
# 可视化散点分布
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x_data[:,0],x_data[:,1],y_data)
# 绘制预期平面
# 构建x
x_0 = x_data[:,0]
x_1 = x_data[:,1]
# 生成网格矩阵
x_0,x_1 = np.meshgrid(x_0,x_1)
y_hat = theta0 + theta1*x_0 + theta2*x_1
# 绘制3D图
ax.plot_surface(x_0,x_1,y_hat)
# 设置标签
ax.set_xlabel("Miles")
ax.set_ylabel("nums")
ax.set_zlabel("Time")
plt.show()
散点图输出如下:
加上拟合回归面后如图所示:

加载全部内容