React Diff算法对比vue
Cobyte 人气:0前言
都说“双端对比算法”,那么双端对比算法,到底是怎么样的呢?跟 React 中的 Diff 算法又有什么不同呢?
要了解这些,我们先了解 React 中的 Diff 算法,然后再了解 Vue3 中的 Diff 算法,最后讲一下 Vue2 中的 Diff 算法,才能去比较一下他们的区别。
最后讲一下为什么 Vue 中不需要使用 Fiber 架构。
React 官方的解析
其实为什么 React 不采用 Vue 的双端对比算法,React 官方已经在源码的注释里已经说明了,我们来看一下 React 官方是怎么说的。
function reconcileChildrenArray(
returnFiber: Fiber,
currentFirstChild: Fiber | null,
newChildren: Array<*>,
expirationTime: ExpirationTime,
): Fiber | null {
// This algorithm can't optimize by searching from boths ends since we
// don't have backpointers on fibers. I'm trying to see how far we can get
// with that model. If it ends up not being worth the tradeoffs, we can
// add it later.
// Even with a two ended optimization, we'd want to optimize for the case
// where there are few changes and brute force the comparison instead of
// going for the Map. It'd like to explore hitting that path first in
// forward-only mode and only go for the Map once we notice that we need
// lots of look ahead. This doesn't handle reversal as well as two ended
// search but that's unusual. Besides, for the two ended optimization to
// work on Iterables, we'd need to copy the whole set.
// In this first iteration, we'll just live with hitting the bad case
// (adding everything to a Map) in for every insert/move.
// If you change this code, also update reconcileChildrenIterator() which
// uses the same algorithm.
}
大概的意思就是说:
React 不能通过双端对比进行 Diff 算法优化是因为目前 Fiber 上没有设置反向链表,而且想知道就目前这种方案能持续多久,如果目前这种模式不理想的话,那么也可以增加双端对比算法。
即使是双端对比算法,我们也要对这种情况进行优化,我们应该使用 Map 这种数据结构方案去替代原来那种几乎没有什么变化也进行暴力比较的方案。它第一次搜索循环是通过 forward-only 这种模式(就是只从左向右查找),(第一次循环可能还没有结束,还有节点没有比对的时候)如果还要继续向前循环查找那么就要通过 Map 这种数据类型了。(就目前这个单向链表的数据结构,如果采用)双端对比查找算法比较难控制它反向查找的,但它确实是一种成功的算法。此外,双端对比算法的实现也在我们的工作迭代当中。
第一次迭代,我们就先将就使用这种不好的方案吧,每次新增/移动都要添加所有的数据到一个 Map 的数据类型对象中。
“we'd need to copy the whole set”,这一句,每一个单词都懂,但就是不知道他想说什么,所以就不翻译了,有知道的大神吗?
本人水平有限,错漏难免,如有错漏,恳请各位斧正。
React 的官方虽然解析了,但我们想要彻底理解到底为什么,还是要去详细了解 React 的 Diff 算法是怎么样的。在了解 React Diff 算法之前,我们首先要了解什么是 Fiber,为什么 React 中要使用 Fiber?
Fiber 的结构
在 React15 以前 React 的组件更新创建虚拟 DOM 和 Diff 的过程是不可中断,如果需要更新组件树层级非常深的话,在 Diff 的过程会非常占用浏览器的线程,而我们都知道浏览器执行JavaScript 的线程和渲染真实 DOM 的线程是互斥的,也就是同一时间内,浏览器要么在执行 JavaScript 的代码运算,要么在渲染页面,如果 JavaScript 的代码运行时间过长则会造成页面卡顿。 基于以上原因 React 团队在 React16 之后就改写了整个架构,将原来数组结构的虚拟DOM,改成叫 Fiber 的一种数据结构,基于这种 Fiber 的数据结构可以实现由原来不可中断的更新过程变成异步的可中断的更新。
Fiber 的数据结构主要长成以下的样子,主要通过 Fiber 的一些属性去保存组件相关的信息。
function FiberNode(
tag: WorkTag,
pendingProps: mixed,
key: null | string,
mode: TypeOfMode,
) {
// 作为静态数据结构的属性
this.tag = tag;
this.key = key;
this.elementType = null;
this.type = null;
this.stateNode = null;
// 用于连接其他Fiber节点形成Fiber树
this.return = null;
this.child = null;
this.sibling = null;
this.index = 0;
this.ref = null;
// 作为动态的工作单元的属性
this.pendingProps = pendingProps;
this.memoizedProps = null;
this.updateQueue = null;
this.memoizedState = null;
this.dependencies = null;
this.mode = mode;
this.effectTag = NoEffect;
this.nextEffect = null;
this.firstEffect = null;
this.lastEffect = null;
// 调度优先级相关
this.lanes = NoLanes;
this.childLanes = NoLanes;
// 指向该fiber在另一次更新时对应的fiber
this.alternate = null;
}
Fiber 主要靠以下属性连成一棵树结构的数据的,也就是 Fiber 链表。
// 指向父级Fiber节点 this.return = null; // 指向子Fiber节点 this.child = null; // 指向右边第一个兄弟Fiber节点 this.sibling = null;
举个例子,如下的组件结构:
function App() {
return (
<div>
i am
<span>Coboy</span>
</div>
)
}
对应的 Fiber 链表结构:
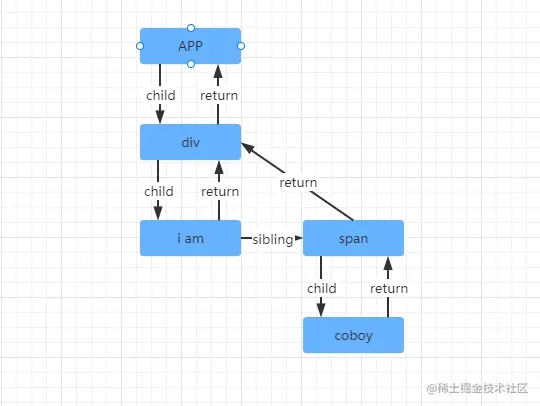
那么以上的 Fiber 链表的数据结构有什么特点,就是任何一个位置的 Fiber 节点,都可以非常容易知道它的父 Fiber, 第一个子元素的 Fiber,和它的兄弟节点 Fiber。却不容易知道它前一个 Fiber 节点是谁,这就是 React 中单向链表 Fiber 节点的特点。也正是因为这些即便在协调的过程被中断了,再恢复协调的时候,依然知道当前的 父节点和孩子节点等信息。
那么 React 是将对应组件怎么生成一个 Fiber 链表数据的呢?
Fiber 链表的生成
上面的组件在经过 JSX 的编译之后,初始化的时候会生成成一个类似于 React 15 或者 Vue 那种虚拟 DOM 的数据结构。然后创建一个叫 fiberRoot 的 Fiber 节点,然后开始从 fiberRoot 这个根 Fiber 开始进行协调,生成一棵 Fiber 树,这个棵树被称为:workInProgress Fiber 树 ,意思是正在工作的 Fiber 树,接下来我们详细了解一下具体是怎么生成一棵 Fiber 树的。要先了解 Fiber 树的生成原理才更好去理解 Fiber 树 diff 的过程。
以下是一段简单版的 Fiber 链表生成的代码片段。 这个协调子节点的函数接收两个参数,returnFiber 是父 Fiber,children 是这个节点的子元素的虚拟 DOM数据。
// 这个协调子节点的函数接收两个参数,returnFiber 是父 Fiber,children 是这个节点的子元素的虚拟 DOM数据。
export function reconcileChildren(returnFiber, children) {
// 如果是字符串或者数字则不创建 Fiber
if(isStringOrNumber(children)) {
return
}
const newChildren = isArray(children) ? children : [children]
// 上一轮的 fiber 节点
let previousNewFiber = null;
// 初次渲染(false)还是更新(true)
let shouldTrackSideEffects = !!returnFiber.alternate
// 老 Fiber 节点
let oldFiber = returnFiber.alternate && returnFiber.alternate.child
let nextOldFiber = null
// 上一次协调返回的位置
let lastPlacedIndex = 0;
// 记录每个 fiber 节点的位置
let newIdx = 0;
// 如果不存在老 Fiber 则是初始化的过程,进行 Fiber 链表的创建
if(!oldFiber) {
for (; newIdx < newChildren.length; newIdx++) {
// 获取节点元素内容
const newChild = newChildren[newIdx]
// 如果节点为 null 则不需要创建 fiber 节点
if(newChild === null) {
continue
}
// 创建新 fiber 的时候记录了关键的父 fiber 等重要信息
const newFiber = createFiber(newChild, returnFiber)
// 记录当前每一个 fiber 的位置
lastPlacedIndex = placeChild(
newFiber,
lastPlacedIndex,
newIdx,
shouldTrackSideEffects // 初次渲染(false)还是更新(true)
)
// 当上一轮的 fiber 节点为 null 的时候,这一轮的 fiber 就是头节点
if(previousNewFiber === null) {
// 父 fiber 的 child 就是第一个节点
returnFiber.child = newFiber
} else {
// 如果不是第一个节点,那么就是兄弟节点
// 上一轮 fiber 的兄弟节点是这一轮的 fiber 节点
previousNewFiber.sibling = newFiber;
}
// 记录上一轮的 fiber,既是这一轮的 fiber 便是下一轮的上一轮 fiber
previousNewFiber = newFiber
}
return
}
}
构建完的 workInProgress Fiber树 会在 commit阶段 渲染到页面。
在组件状态数据发生变更的时候,会根据最新的状态数据先会生成新的虚拟DOM,再去构建一棵新的 workInProgress Fiber 树 ,而在重新协调构建新的 Fiber 树的过程也就是 React Diff 发生的地方。接下来,我们就看看 React Diff 算法是怎么样的。
React 的 Diff 算法
深度优先,有子节点,就遍历子节点,没有子节点,就找兄弟节点,没有兄弟节点,就找叔叔节点,叔叔节点也没有的话,就继续往上找,它爷爷的兄弟,如果一直没找到,就代表所有的更新任务都更新完毕了。
重点是在更新自己的同时需要去协调子节点,也就是传说中进行 Diff 的地方。
进入协调的时候它自己就是父 Fiber,它的子节点在协调之前,是刚刚通过更新的状态数据生成的最新的虚拟DOM数据,是个数组结构的元素数据。
那么要进行更新,就肯定是以为最新的节点数据为准了,又因为最新的节点数据是一个数组,所以可以进行循环对比每一个节点,很明显这个循环是从左向右进行查找比对的。
第一轮,常见情况的比对
那么第一个节点的老 Fiber 怎么拿到呢?可以通过 父 Fiber 的 child 属性拿到,这样第一个节点的老 Fiber 就拿到了,那么第二节点的老 Fiber,很明显可以通过第一个节点的老 Fiber 节点的 sibling 属性拿到,后面的以此类推。
怎么比对呢?
在循环的新节点虚拟DOM数据的时候,拿到新节点虚拟DOM信息,然后就去和老 Fiber 节点进行比对,如果两个节点相同则创建一个新的 Fiber 节点并复用一些老 Fiber 节点的信息,比如真实 DOM,并给这个新的 Fiber 节点打上一个 Update 的标记,代表这个节点需要更新即可。
接着去更新协调位置信息。
在循环的最后进行 Fiber 链表的处理:
如果是头节点,则把新 Fiber 设置为父 Fiber 的 child 属性的值; 如果不是头节点,则把新 Fiber 设置为上一轮循环的创建的 Fiber 节点的 sibing 属性的值; 更新上一轮 Fiber 变量的值,就是把这一轮的 Fiber 设置成下一轮的 Fiber; 更新比对的老 Fiber 的值。
如果新节点都能找到能复用的节点,则判断是否还存在老节点,有则删除。
第二轮,不常见的情况的比对
如果经过第一轮比对,新节点还存在未比对的,则继续循环查找。
先将剩下未比对的老 Fiber 节点全部处理成一个 老 Fiber 的 key 或老 Fiber 的 index 为 key,Fiber 节点为 value 的 Map 中,这样就可以,以 O(1) 复杂度,通过新 Fiber 的 key 去 Map 对象中查找匹配的 Fiber,找到了,则删除 Map 对象中的老 Fiber 数据,然后复用匹配到的 Fiber 数据。
接下来,不管有没有匹配到都进行位置协调,记录最新的位置信息,新增的 Fiber 因为没有存在老 Fiber 而会被打上 Placement 的标记,在将来提交的阶段将会被进行新增操作。这个过程跟第一轮最后的处理是一样的。
在循环的最后进行 Fiber 链表的处理:
如果是头节点,则把新 Fiber 设置为父 Fiber 的 child 属性的值; 如果不是头节点,则把新 Fiber 设置为上一轮循环的创建的 Fiber 节点的 sibing 属性的值; 更新上一轮 Fiber 变量的值,就是把这一轮的 Fiber 设置成下一轮的 Fiber; 更新比对的老 Fiber 的值。
重点如何协调更新位置信息
如果是初始渲染,那么协调位置就只是记录当前元素下标的位置到 Fiber 节点上。如果是更新阶段,就先判断有没有老 Fiber 节点,如果没有老 Fiber 节点,则说明该节点需要创建,就给当前新的 Fiber 节点打上一个 Placement 的标记,如果有老 Fiber 节点,则判断老 Fiber 节点的位置是否比上一次协调的返回的位置小,如果是,则说明该节点需要移动,给新 Fiber 节点打上一个 Placement 的标记,并继续返回上一次协调返回的位置;如果老 Fiber 节点的位置大或者等于上一次协调返回的位置,则说明该节点不需要进行位置移动操作,就返回老 Fiber 的位置即可。
这里需要说明的一点,为什么移动和新增节点都是 Placement 的标记呢?
因为我们是在协调一个子节点列表,所以不管是新增还是移动都是属于位置是需要发生变化的,所以新增和移动都是同一种操作情况。
小结
总个来说,React Diff 算法分以下几个步骤:
- 第一轮,从左向右新老节点进行比对查找能复用的旧节点,如果有新老节点比对不成功的,则停止这一轮的比对,并记录了停止的位置。
- 如果第一轮比对,能把所有的新节点都比对完毕,则删除旧节点还没进行比对的节点。
- 如果第一轮的比对,没能将所有的新节点都比对完毕,则继续从第一轮比对停止的位置继续开始循环新节点,拿每一个新节点去老节点里面进行查找,有匹配成功的则复用,没匹配成功的则在协调位置的时候打上 Placement 的标记。
- 在所有新节点比对完毕之后,检查还有没有没进行复用的旧节点,如果有,则全部删除。
图文解释 React Diff 算法
接下来我们使用图文进行 React Diff 算法讲解,希望可以更进一步了解 React 的 Diff 算法。
最简单的 Diff 场景
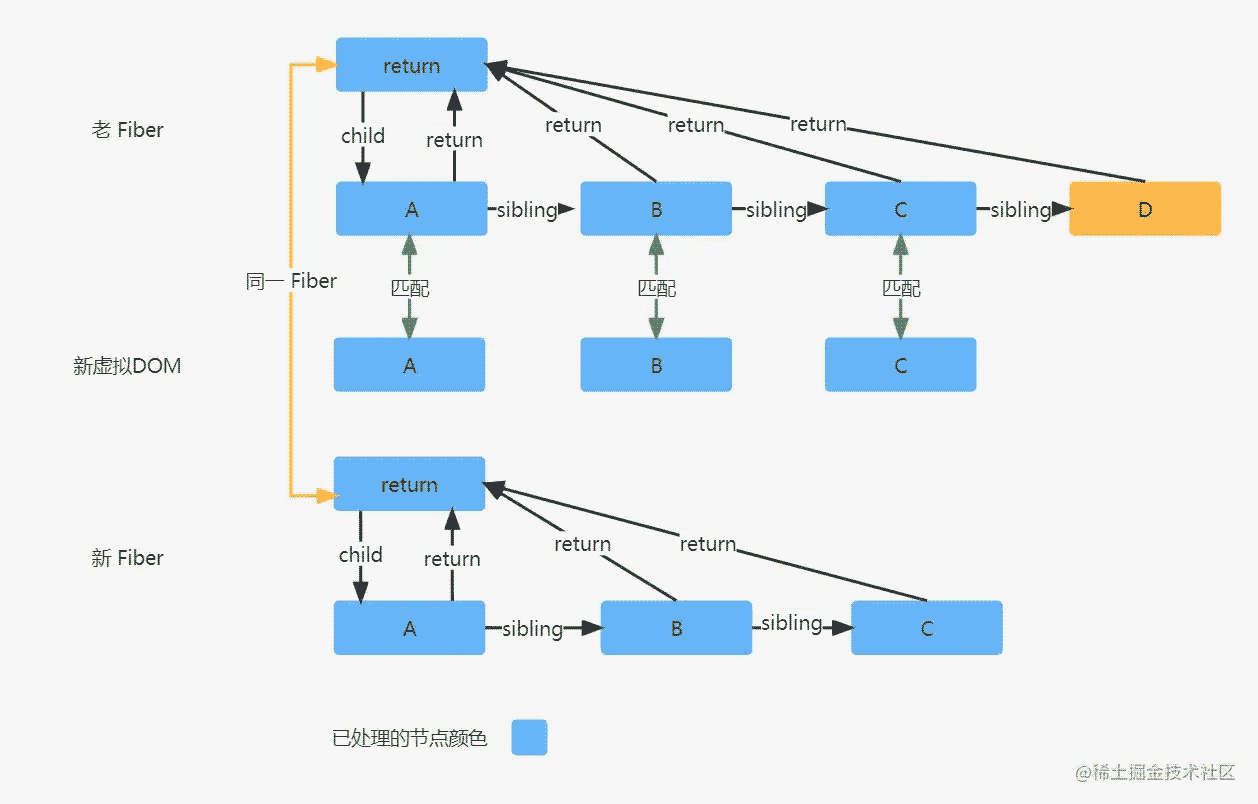
上图的 Diff 场景是最简单的一种,新虚拟DOM 从左到右都能和老 Fiber 的节点一一匹配成功,协调位置的时候,老 Fiber A 的位置是 0,默认上一次协调返回的位置也是 0,根据协调位置规则,老 Fiber 的位置不比上一次协调返回的位置小,则只需要返回老 Fiber A 的位置 0 即可;
到了 B 进行协调位置的时候,老 Fiber B 位置 1 不比上一次协调返回的位置 0 小,则只需返回老 Fiber B 的位置 1 即可;到了 C 进行协调位置的时候,老 Fiber C 位置 2 不比上一次协调返回的位置 1 小,则只需要返回老 Fiber C 的位置 2 即可;
最后全部的新虚拟DOM 比对完毕,但老 Fiber 上还存在节点信息,则需要将剩下的老 Fiber 进行删除标记。
接下来我们看看复杂的 Diff 场景。
复杂的 Diff 场景
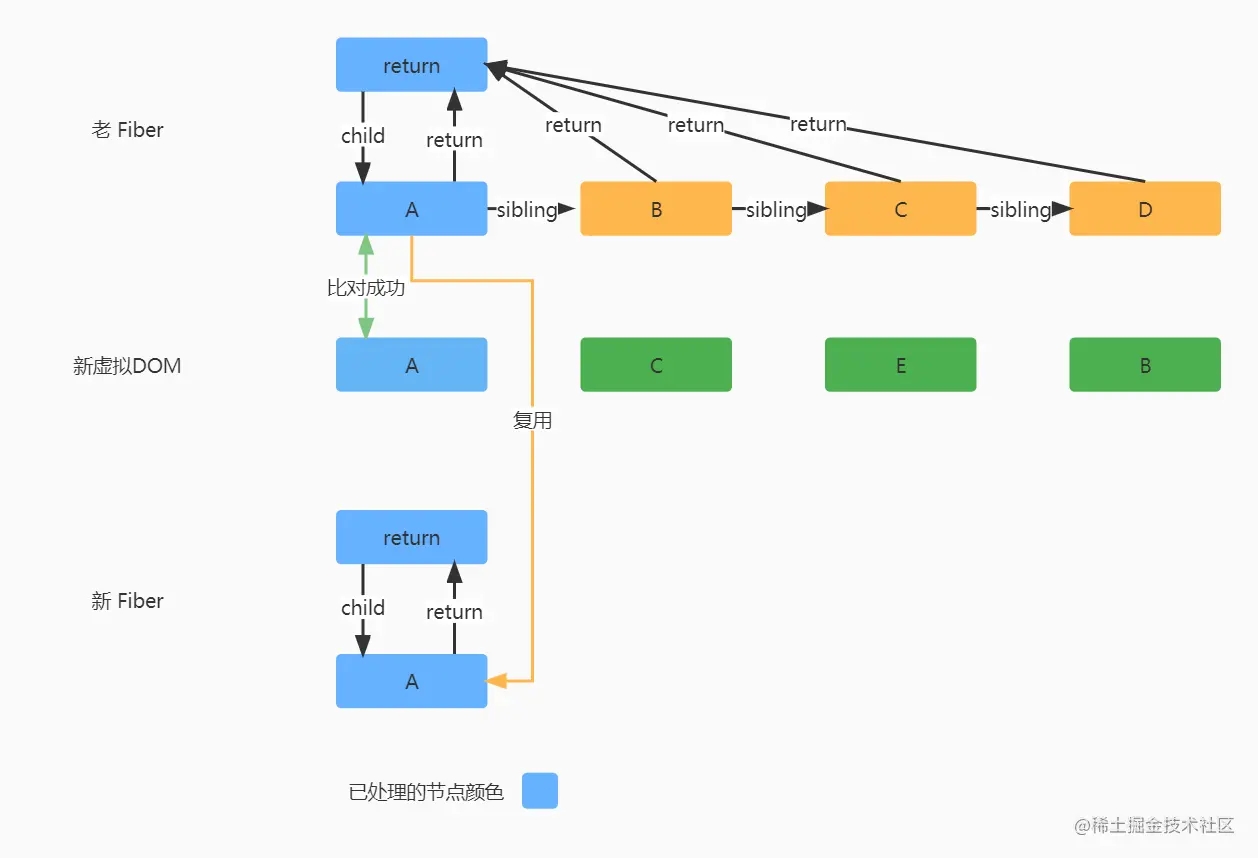
在上图中,第一轮循环比对的时候,新虚拟节点A 和第一个老 Fiber 节点是可以匹配的,所以就可以复用老 Fiber 的节点信息了,并且在协调的位置信息的时候,是存在老 Fiber 的,那么就去比较老 Fiber 的位置和上一次协调返回的位置进行比较(上一次协调返回的位置默认为 0),老 Fiber 的位置是等于新 Fiber 的位置,根据协调规则,位置不需要移动,返回老 Fiber 的位置信息即可,很明显这次返回的协调位置是 0。
到了第二个新虚拟节点 C 的时候,C 和老 Fiber 中的 B 是不匹配的,则第一轮比对结束。
第一轮比对结束之后,新虚拟DOM是还存在未比对的节点的,那么继续开始第二轮的比对。
在第二轮比对开始之前,会先将剩下未比对的老 Fiber 节点全部处理成一个 老 Fiber 的 key 或老 Fiber 的 index 为 key,Fiber 节点为 value 的 Map 中。
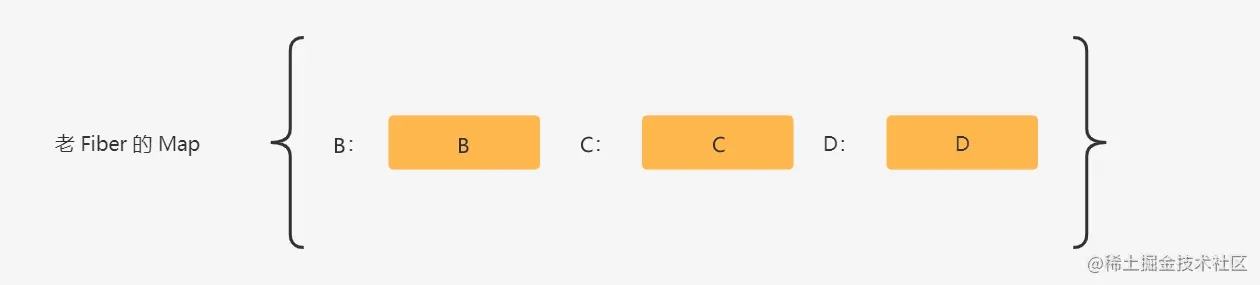
然后进行第二轮的比对。
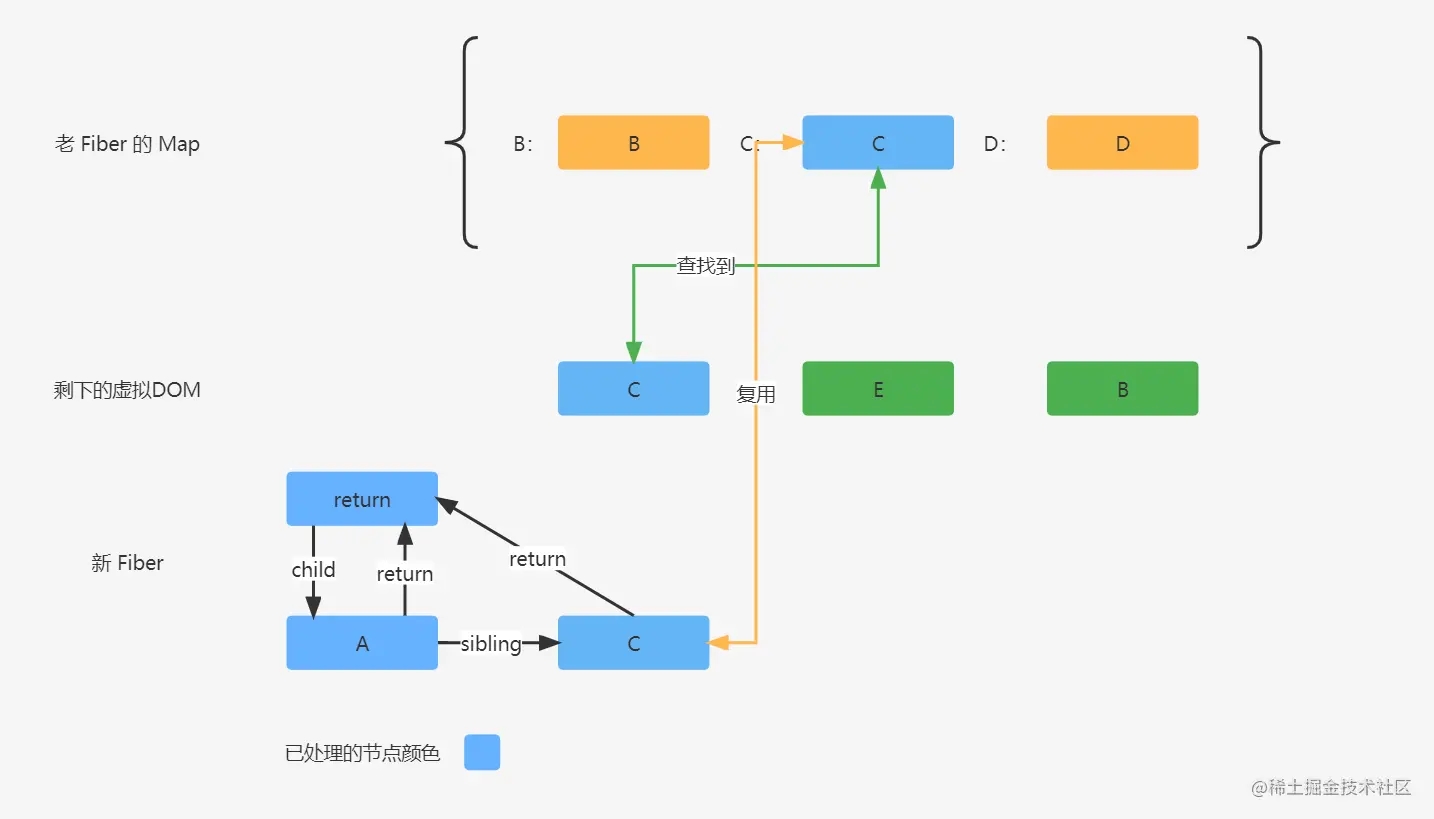
虚拟DOM C 可以通过 C 的 key 值在老 Fiber 的 Map 中找到老 Fiber C 节点,这个时候会 C 进行暂存,然后把 Map 中的 C 进行删除,再进行老 Fiber 的节点信息复用,然后去协调比对位置信息。
老 Fiber C 的位置是 2,然后上一次新 Fiber A 协调比对返回的位置信息是 0,那么这一次协调的位置是老 Fiber 的位置比上一次协调返回的位置大,那么这次协调是不用标记 Placement 标记的,直接返回老 Fiber C 的位置 2。
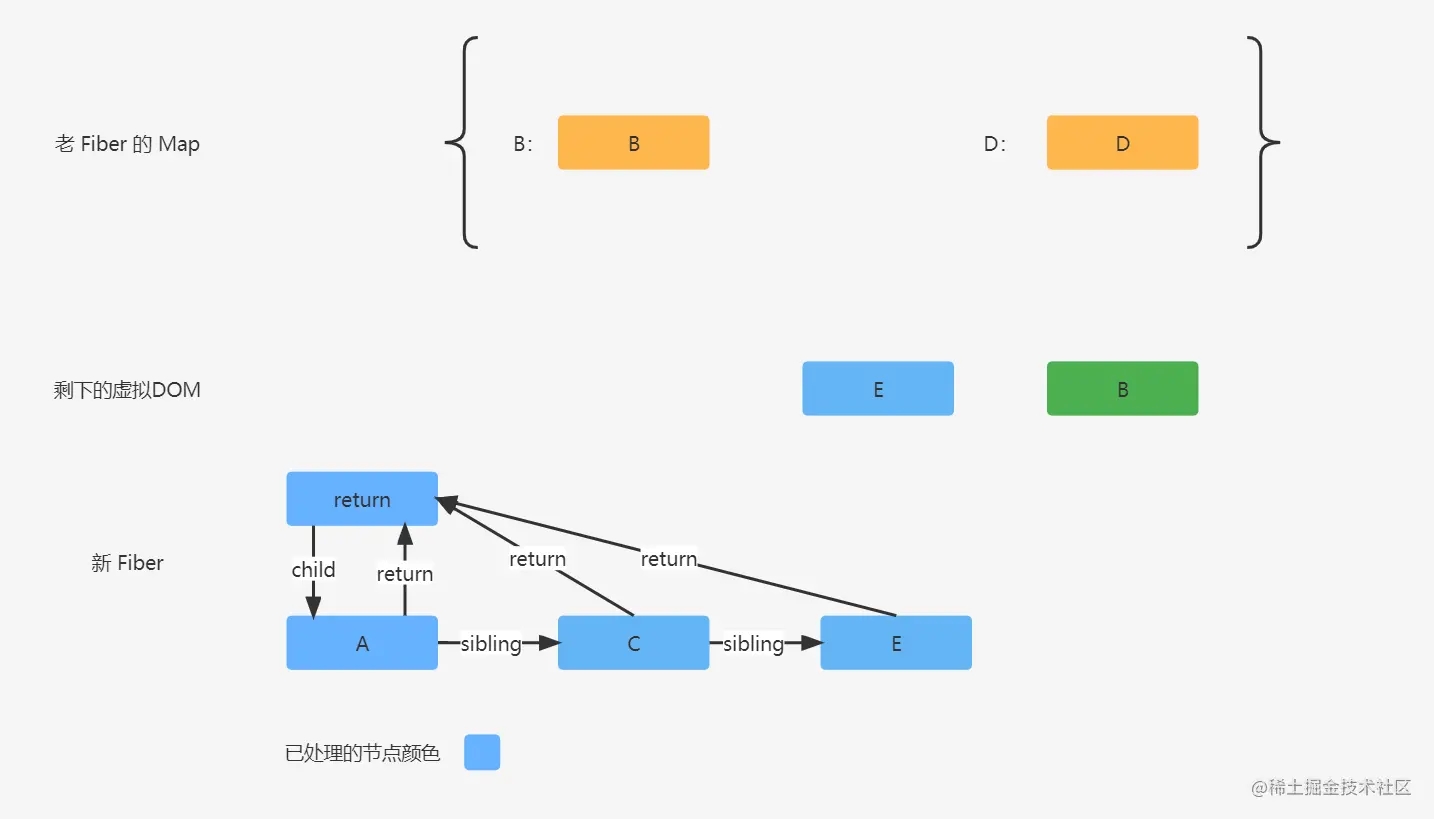
虚拟DOM E,在老 Fiber 的 Map 中是没有匹配成功的,所以在创建 Fiber E 的时候,是没有进行老 Fiber 的复用的,去协调比对位置的时候,根据协调位置规则,没有老 Fiber,就标记 Placement 并返回上一次协调返回的位置,那么上一次 C 协调位置返回的位置信息是 2,这一次 E 协调位置依然返回 2。
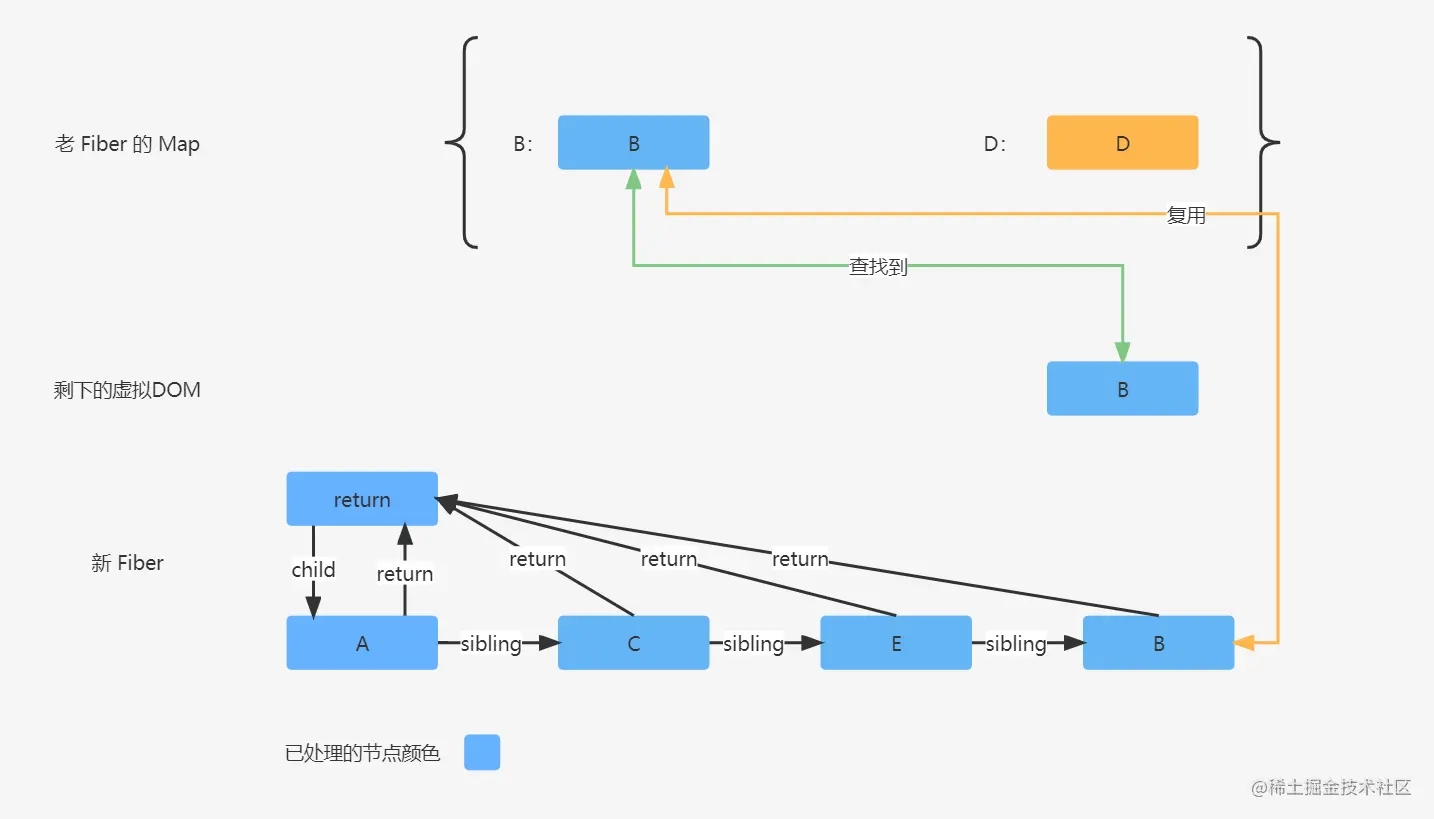
虚拟DOM B 也在 Fiber 的 Map 中匹配成功了,那么匹配成功之后,就对老 Fiber B 进行暂存,然后删除老 Fiber B,再进行信息复用,然后又进行位置协调,老 Fiber B 的位置是 1,上一次协调返回的位置是 2,根据协调位置规则,老 Fiber 的位置小于上一次协调返回的位置,则标记 Placement 并返回上一次协调返回的位置 2。

最后,老 Fiber 的 Map 中还存在一个 D 节点没处理,则需要对其进行删除标记操作。
最终新 Fiber 将被协调成下面的样子:
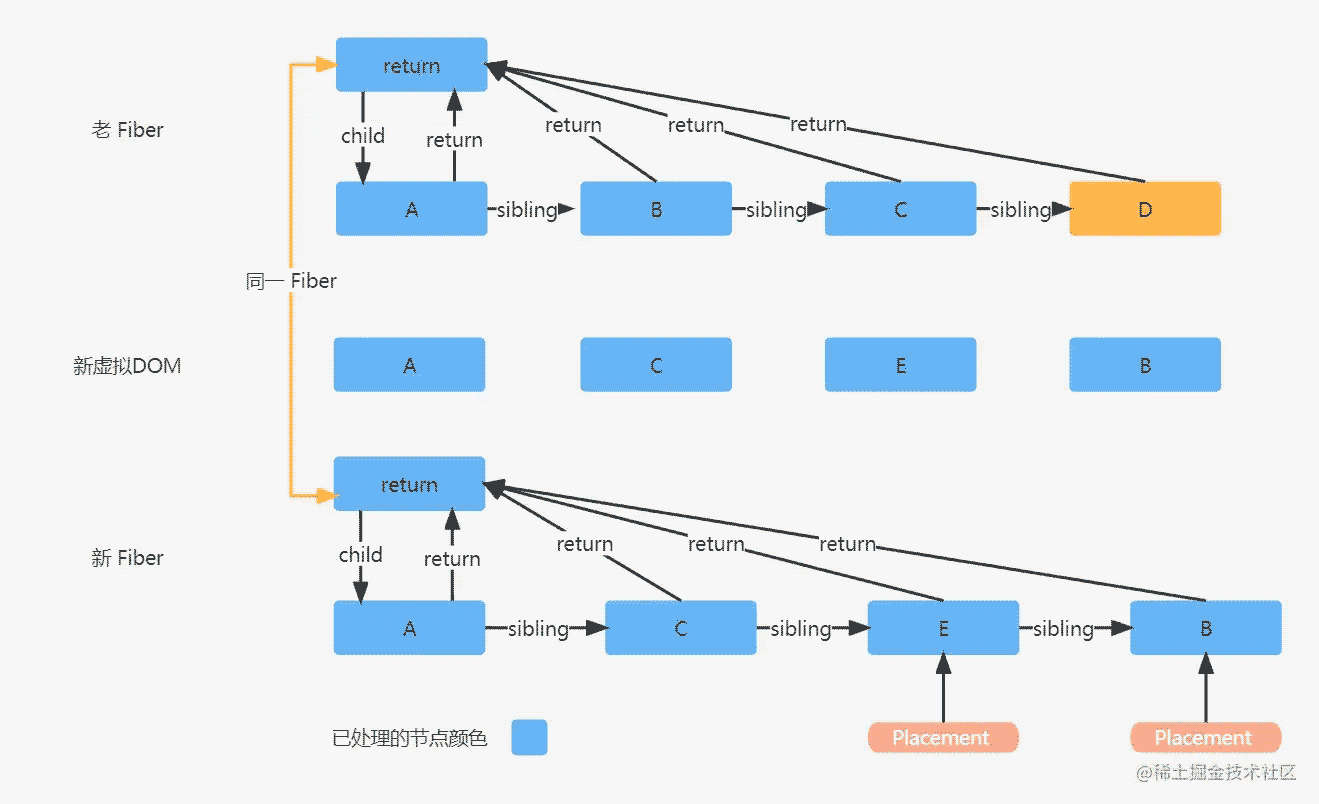
那么根据图片,我们又可以得出一个结论,匹配到的老 Fiber 如果和新 Fiber 相同或者在新 Fiber 位置的右边则不需要进行移动标记。
Vue3 的 Diff 算法
在我看来 Vue3 的 Diff 算法是 Vue2、Vue3、React 的 Diff 算法中最复杂的一种。 下面我们来简单说一下 Vue3 的 Diff 算法,只说数组和数组比对的情况。
第一轮,常见情况的比对
首先从左往右进行比对,如果是相同的就进行更新比对,如果不相同则停止比对,并且记录停止的下标。 再从右往左进行比对,如果是相同的就进行更新比对,如果不相同也停止比对,也进行记录停止的下标。 通过这样左右进行比对,最后就可以把真正复杂部分进行范围锁定了。 左右比对完之后,如果新节点已经比对完了,老节点列表还存在节点未比对,则删除老节点列表上的未比对的节点,如果老节点已经比对完了,新节点列表还存在未比对的节点则进行创建。
第二轮,复杂情况的比对
如果新节点未比对完,老节点也未比对完,则进行最后最复杂的处理。
先把剩下的新节点处理成节点的 key 为 key, 节点下标为 value 的 Map; 接着初始化一个长度为剩下未比对的新节点的长度的数组 newIndexToOldIndexMap,初始化每个数组的下标的默认值为 0。 再循环剩下的旧节点,通过旧节点的 key 去刚刚创建的 Map 中查找,看看旧节点有没有在新节点中,如果旧节点没有 key 则需要通过循环剩下的新节点进行查找。 如果旧节点在新节点中没找到,则说明该旧节点需要进行删除。 如果找到了,则把找到的新节点的下标对应存储到上述的数组 newIndexToOldIndexMap 中,然后更新比对匹配到的新老节点。
把所有的旧节点比对完成后,就会得到一个刚刚收集的新节点的下标数组,然后对这个新节点的下标数组进行进行最长递增子序列查找得到一个最长递增子序列的下标数据。 然后再进行循环左右对比完之后剩余新节点的下标,然后判断循环的下标是否被上述的数组 newIndexToOldIndexMap 进行收集了,如果没被收集到则说明这个新节点需要进行创建,如果已经被收集了则判断该循环的下标是否在上面计算得到的最长递增子序列中,如果不在则需要对该循环节点进行移动操作。
加载全部内容