C语言交换排序算法

时间:2022-09-27 白滴岑人气:0

前言

查找和排序是数据结构与算法中不可或缺的一环，是前辈们在算法道路上留下的重要且方便的一些技巧，学习这些经典的查找和排序也能让我们更好和更快的解决问题。在这个专栏中我们会学习六大查找和十大排序的算法与思想，而本篇将详细讲解其中的交换排序——冒泡排序和快速排序；

注意：本文中所有排序按照升序排序，降序只需要把逻辑反过来即可！

一、冒泡排序

1.基本思想

对于很多同学来说冒泡排序是再熟悉不过了，冒泡的思想在于：不断的比较两个元素并交换，大的在右边，小的在左边；

有一个数组{5, 1, 4, 2, 8, 4}

第一轮

arr[0] = 5和 arr[1] = 1比较 5 > 1，交换；
arr[2] = 4和 arr[1] = 5比较 5 > 4，交换；
arr[2] = 5和 arr[3] = 2比较 5 > 2，交换；
arr[3] = 5和 arr[4] = 8比较 5 < 8，不交换；
arr[4] = 8和 arr[5] = 4比较 8 > 4，交换；

第二轮

从arr[1]开始重复上述的步骤；

... ...直到循环 N - 1 次，排序结束；

#include <stdio.h>
#include<stdlib.h>
 
//冒泡排序
void bubbleSort(int a[], int n)
{
    //一共要扫描n-1趟
    for(int i = 0; i < n - 1; i++)
    {
        //用来比较 交换
        for(int j = 0; j < n - i - 1; j++)
        {
            if(a[j] > a[j + 1])
            {
                int temp = a[j + 1];
                a[j + 1] = a[j];
                a[j] = temp; 
            }
        }
    }
}
 
int main()
{
    int arr[] = {5, 1, 4, 2, 8, 4};
    int length = sizeof(arr) / sizeof(arr[0]);
    bubbleSort(arr, length);
    for(int i = 0; i < length; i++)
    {
        printf("%d", arr[i]);
    }
    system("pause");
    return 0;
}

那么问题来了，问题一：这里我们发现对于这个数组而言在第二轮排序就已经排好了整体甚至稳定的有序，剩下的循环就相当于浪费了，那么有没有一种方法能够判断数组已经有序？

还有这样一个数组{4, 2, 1, 5, 6, 8}

问题二：我们发现{5, 6, 8}的部分是已经有序了的，对于已经有序的部分还要继续比较，那么能不能确定出有序的部分和无序的部分的边界呢？

2.优化

针对问题一，我们可以添加一个标志，用来标识数组是否有序：当某一轮排序没有发生交换，就可以认为数组已经有序了；

针对问题二，我们可以记录冒泡排序的过程中最后一次发生交换的地方index，如在下图中index==1，每一次后面的排序只要从第一个到index就可以了；

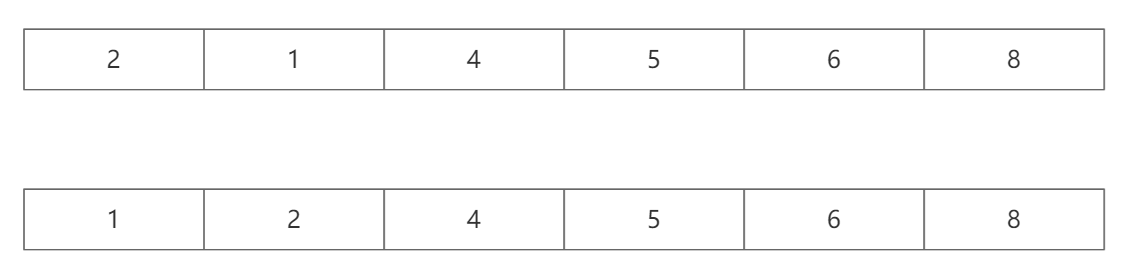
值得注意的是，不管怎样去优化，最坏情况的时间复杂度都是O(n^2)，即数组逆序的情况；

3.扩展

虽然用栈实现冒泡排序可能在实际中没有应用场景（也没必要用），但是可能会有面试的时候要求用栈或者其他的结构去实现冒泡排序来考查对算法和思想熟练度，所以这里也提供用栈实现冒泡排序的思路；

void bubbleSort(int a[], int n)
{
    //定义两个栈S1和S2
    stack<int>stk1, stk2;
    //将数组中的所有元素入栈S1
    for (int i = 0; i < n; i++)
    {
        stk1.push(a[i]);
    }
    //循环N次 每一次找出最大的元素（就像真冒泡一样 最大的元素浮在最上面）
    for (int i = 0; i < n; i++)
    {
        //如果S1不为空
        while (!stk1.empty())
        {
            //如果S2为空就把栈S1顶的元素入栈S2
            if (stk2.empty())
            {
                stk2.push(stk1.top());
                stk1.pop();
            }
            else
            {
                int temp = 0;//用于接收需要交换的元素
                if (stk1.top() < stk2.top())
                {
                    //如果S1的栈顶小于S2的栈顶 把S1的栈顶压在S2的栈顶下面
                    temp = stk2.top();
                    stk2.pop();
                    stk2.push(stk1.top());
                    stk1.pop();
                    stk2.push(temp);
                }
                else
                {
                    stk2.push(stk1.top());
                    stk1.pop();
                }
            }
        }
        //把最大的元素从后往前更新回原数组中
        a[n - i - 1] = stk2.top();
        stk2.pop();
        //把剩下的元素倒栈 重复
        for (int j = stk2.size(); j > 0; j--)
        {
            stk1.push(stk2.top());
            stk2.pop();
        }
    }
}

二、快速排序

1.基本思想

选取一个基准（可以认为是要放到排序以后正确的位置的元素，可以是第一个元素、最后一个中间的、随机的都可以）；

把数组中的元素做一个划分，每一趟划分将作为基准的值x放到排序后数组正确的位置，并将所有比x小的放到左边，比x大的放到右边；

有一个数组{1, 8, 3, 9, 4, 5, 4, 7}

假定选择元素arr[7] = 7为基准，就是要把7放在正确的位置，那么只有两种情况：

要么7本身就是正确的位置，要么就在前面；

第一步：初始化指针 i = -1，j = 0，把 j 指向的元素和7比较，当1 < 7，将 i++，交换 i 和 j 指向的元素，j++；

第二步：把 j 指向的元素和7比较，当8 > 7，将 j++；

第三步：把 j 指向的元素和7比较，当3 < 7，将 i++，交换 i 和 j 指向的元素，j++；

第四步：把 j 指向的元素和7比较，当4 < 7，将 i++，交换 i 和 j 指向的元素，j++；

第五步：把 j 指向的元素和7比较，当5 < 7，将 i++，交换 i 和 j 指向的元素，j++；

第五步：把 j 指向的元素和7比较，当4 < 7，将 i++，交换 i 和 j 指向的元素，j++；

第六步：当j到7遍历结束，让i++的位置和7交换，第一趟排序结束；

如此一来，基准7就找到了它在数组中的正确位置，并且把数组划分成了两边【0，5）和（5,7】这时再选一个基准再进行上述步骤，如下图所示：

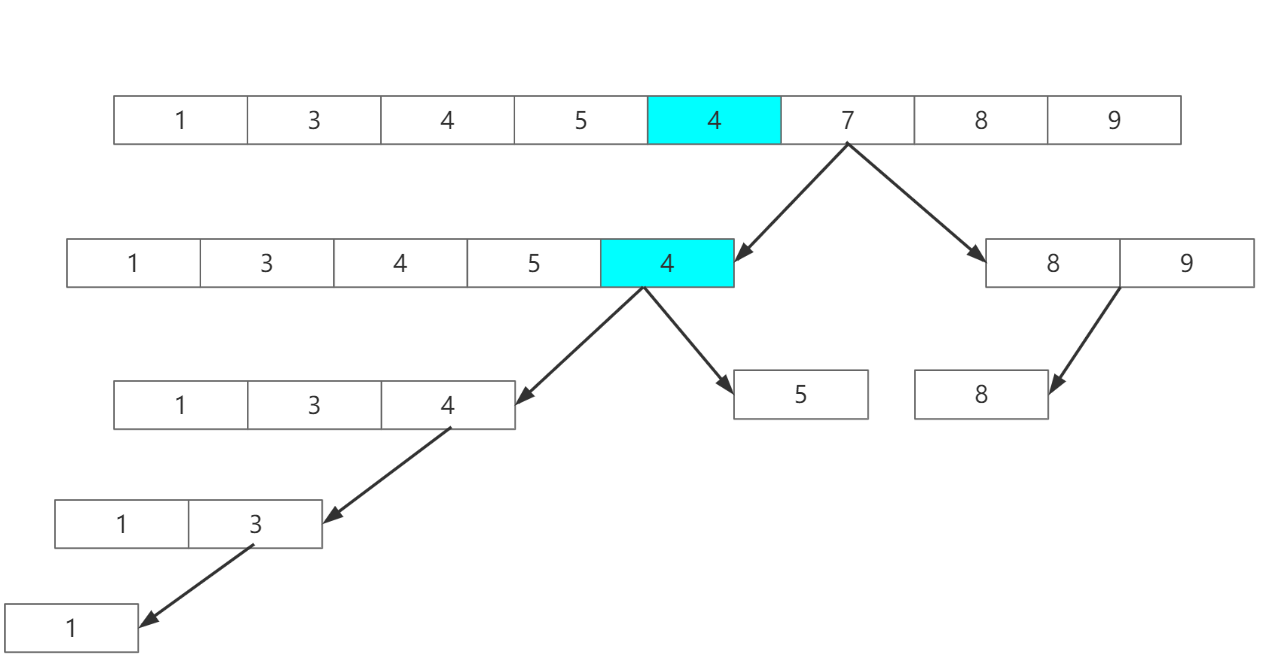
是不是觉得很眼熟？没错这就是一棵二叉树：

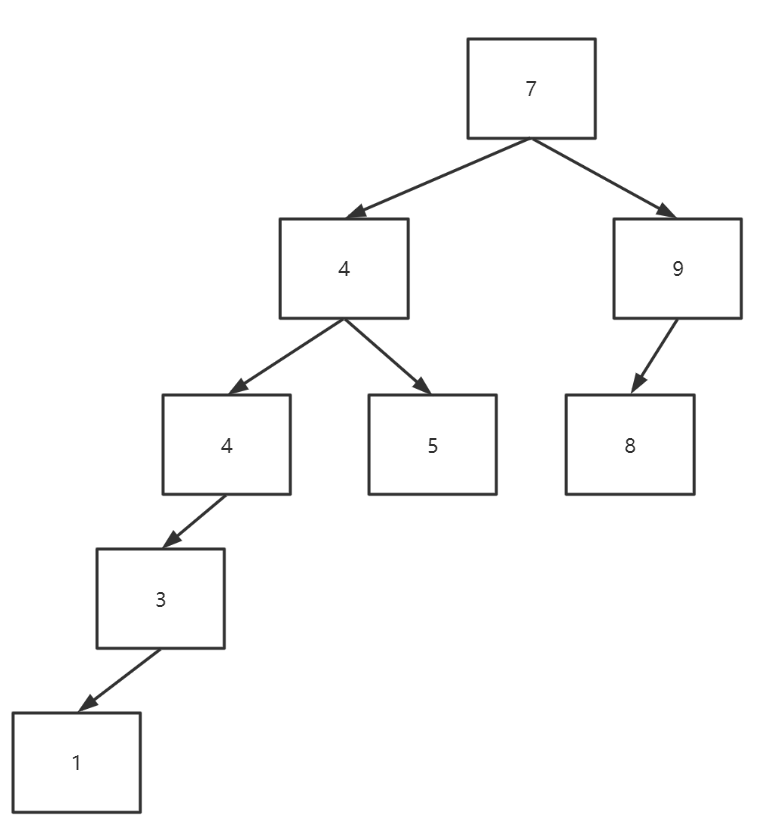
2.优化

既然是二叉树，那么排出一棵斜树自然就是最坏的情况；要缓解这个问题，可以以中间的值为基准来减少这种情况的发生；

即复杂度与数组长度和基准的选择有关，尾基准是O(n^2)因为n趟每一趟划分需要O(n)，而平衡树是O(nlogn)，通过数学方法能够得到更优的基准选择，但无论选什么为基准都应该能满足：基准左边小、右边大；

我们之前说过，快速排序其实是一个不稳定排序（不稳定的排序就意味着交换的次数多，如果需要按多条件排序就会乱），而我们又说过任何一个不稳定的排序算法都有办法使其变得稳定，用到的是以空间换时间的思想；

也就是我们可以用一个变量对原来的顺序做标记；

3.代码

既然是通过不断划分数组来减少比较的次数，这一听就知道用到了分治的思想，也就是可以用递归来实现代码：

#include <stdio.h>
#include<stdlib.h>
 
//快排
void quickSort(int a[], int low, int high)
{
   if(low < high)
   {
        int i = low;//这里以i下标的值为基准
        int j = high;
        int k = a[low];//k是用来记录基准的值
        while(i < j)
        {
            //从右往左找第一个比k要小的值
            while(i < j && a[j] >= k)
            {
                j--;
            }
            if(i < j)
            {
                a[i++] = a[j];
            }
            //从左往右找第一个比k要大的值
            while(i < j && a[i] < k)
            {
                i++;
            }
            if(i < j)
            {
                a[j--] = a[i];
            }
        }
        a[i] = k;
        //递归
        quickSort(a, low, i - 1);
        quickSort(a, i + 1, high);
   }
}
 
int main()
{
    int arr[] = {1, 8, 3, 9, 4, 5, 4, 7};
    int length = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, length - 1);
    for(int i = 0; i < length; i++)
    {
        printf("%d ", arr[i]);
    }
    system("pause");
    return 0;
}

运行结果

加载全部内容